4,40 von 5 Sterne
Loading...
Du hast das Wort Varianz zwar schon einmal gehört, kannst den Begriff aber nicht genau zuordnen? In diesem Artikel erklären wir dir alles, was du zu dem Thema wissen musst.
Hier erfährst du z.B. alles über die Definition, wie man sie berechnet und was der Unterschied zur verwandten Standardabweichung ist.
Los geht’s!
Sie zeigt an, wie sich die Beobachtungswerte um den Mittelwert herum bei einer Beobachtung verteilen. Sie gehört somit zu den Streuungsmaßen.
Mit anderen Worten kann man auch sagen, dass sie die durchschnittliche Abweichung von ihrem Erwartungswert in einer Beobachtung ist.
Varianz Formel
Die Formel sieht folgendermaßen aus:
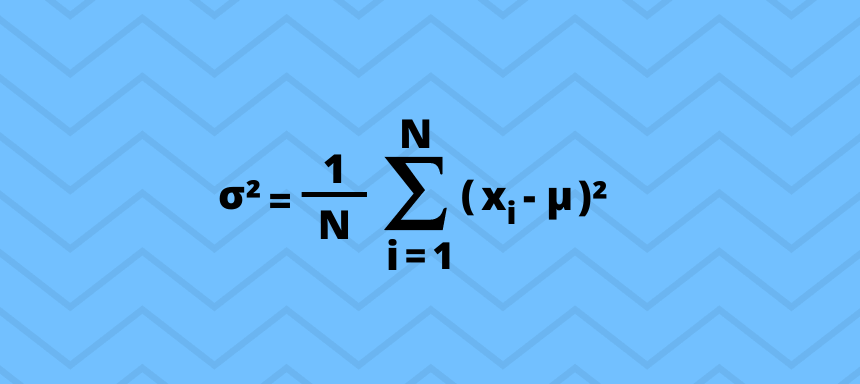
σ² = Varianz
N = Gesamtzahl
x i = Beobachtungszahl
μ = Mittelwert (arithmetisches Mittel)
Um die theoretische Formel anschaulicher zu gestalten, haben wir im nächsten Abschnitt ein einfaches Beispiel gegeben.
Varianz Beispiel
Im folgenden wurden 5 Personen gefragt, wieviel Zeit sie in der Woche mit lernen verbringen:
Person | 1 | 2 | 3 | 4 | 5 |
Stunden Lernen pro Woche | 3 | 2 | 7 | 5 | 3 |
Zunächst einmal, berechnen wir den Mittelwert und setzen das Ergebnis anschließend in die Formel ein:
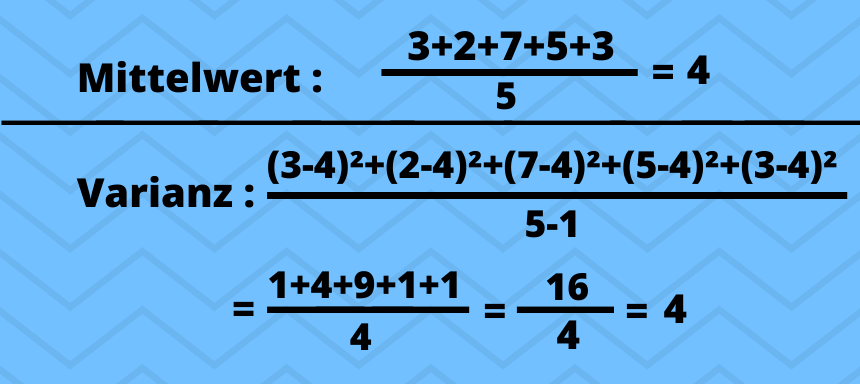
Falls dieses Beispiel zu schnell ging, haben wir noch einmal eine ausführliche Erklärung im nächsten Kapitel.
Varianz berechnen – in 5 Schritten
Um die Berechnung noch einmal ausführlich aufzuzeigen, haben wir im Folgenden ein neues Beispiel in 5 Schritte aufgeteilt.
Diesmal geht es um die Befragung von 8 Personen nach ihrem Alter:
Person | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
Alter | 23 | 43 | 19 | 20 | 37 | 45 | 23 | 55 |
Schritt 1 – Mittelwert
Zuerst einmal, muss der Mittelwert der Beobachtungswerte erstellt werden.
Dazu werden alle Altersangaben addiert und durch die Gesamtanzahl der Personen geteilt:
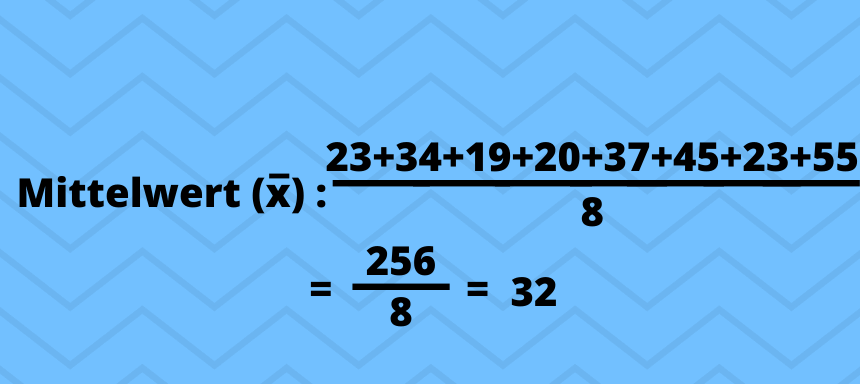
Schritt 2 – Abweichung Beobachtungswerte
Im nächsten Schritt berechnen wir die Abweichungen der Beobachtungswerte vom Mittelwert.
Dazu subtrahieren wir den Mittelwert von den jeweiligen Beobachtungswerten:
Schritt 3 – Ergebnisse quadrieren
Da die Varianz NIE negativ sein kann, müssen wir die Ergebnisse quadrieren.
Die Werte aus Schritt 2 müssen nun hoch 2 gerechnet werden:
Schritt 4 – Summe der Abweichungen
Anschließend müssen wir die Summe der quadrierten Abweichungen bilden.
Hierfür addieren wir alle Ergebnisse aus Schritt 3:
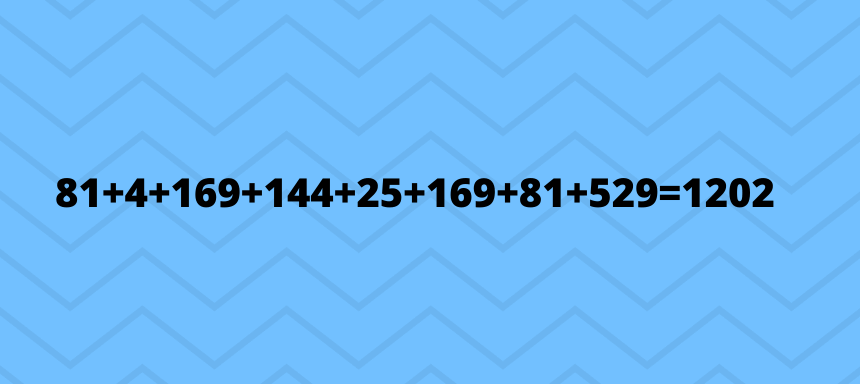
Schritt 5 – Varianz berechnen
Nun nehmen wir die Gesamtzahl der Beobachtungen minus 1 und teilen die Summe aus Schritt 4 durch diese Zahl:
Aber ist das jetzt ein aussagekräftiges Ergebnis? Und was ist überhaupt die Einheit Jahre²?
Dafür benötigen wir nun die Standardabweichung.
Varianz Standardabweichung
Die Standardabweichung ist ein deutlich aussagekräftigerer Wert. Sie ist eigentlich nichts anderes als die Wurzel der Varianz. Um aus Jahre² also die normalen Jahre zu erhalten, ziehen wir die Wurzel:
Varianz = 171,71 Jahre^2
Standardabweichung = √171,71 = 13,1 Jahre
Nun haben wir mit dem jahreswert von 13,1 Jahre ein aussagekräftiges Ergebnis über die Streuung.
13,1 Jahre liegen die Beobachtungswerte durchschnittlich vom Mittelwert entfernt.
Varianz Rechner
Wenn dir mal die Zeit oder die Lust fehlt, eine ausführliche Rechnung durchzuführen, kannst du auch einen Online Rechner benutzen:
Dort kannst du deine Zahlen eingeben und schnell ein ausführliches Ergebnis erhalten.
Quiz
Ergebnisse
#1. Was zeigt die Varianz an?
#2. Die Varianz kann auch negativ sein. Richtig oder falsch?
#3. Was muss man mit der Varianz machen, um die Standardabweichung zu erhalten?
#4. Gegeben ist das Einkommen von 4 Personen: 1. 2000€ 2. 1800€ 3. 2500€ 4. 1200€, Wie lautet der Mittelwert?
FAQ
Was sagt die Varianz aus Beispiel?
Die Varianz zeigt an, wie sich die Beobachtungswerte um den Mittelwert bei einer Beobachtung herum verteilen. Sie gehört somit zu den Streuungsmaßen.
Wann Varianz berechnen?
Die Varianz berechnet man, wenn man die durchschnittliche Abweichung zu dem Mittelwert berechnen will. Außerdem benötigt man die Varianz, wenn man die darauf folgende Standardabweichung berechnet will.
Was bedeutet eine Varianz von 0?
Die Varianz ist durch die Quadrierung der Abweichungen folglich immer größer oder gleich Null. Bei der Portefeuilletheorie bedeutet die Varianz z.B. das Risiko. Bei einer Varianz von Null bedeutet dies, dass es kein Risiko gibt.
Falls du bis hierhin gelesen hast, bedanken wir uns schonmal sehr dafür.
Wir hoffen der Artikel hat dir geholfen, um bei der nächsten Klausur gut abzuschneiden.
Falls du noch einen konstruktiven Beitrag oder einen anderen Kommentar hinterlassen möchtest, kannst du dies gerne tun. 🙂
Zu guter Letzt…
Wären wir dir noch sehr, sehr dankbar, wenn du uns noch eine Sternebewertung hinterlassen könntest.
Das würde unserer Arbeit sehr helfen!
4,40 von 5 SterneLoading...
Die Formel zur Berechnung der Varianz ist falsch.
Der Faktor vor Sigma … ist nicht 1/N, sondern 1/(N-1)
Da liegst du leider falsch. Was du meinst bezieht sich auf die empirische Varianz oder korrigierte Stichprobenvarianz. In unserem Artikel beziehen wir uns auf die Varianz in der Grundgesamtheit. Dafür brauchst du nur 1/n teilen. Hoffentlich konnten wir dir weiterhelfen 🙂
Ich bin fast 71 Jahre alt und meine erste Statistik-Vorlesung liegt nun 51 Jahre zurück. Es ist sehr interessant, sich noch einmal damit zu beschäftigen. Ich finde Ihre Herangehensweise sehr gut und werde Ihr Medium weiter benutzen, um meine grauen Gehirnzellen fit zu halten.
Vielen Dank!