Du möchtest wissen, wie du mit der Summenregel Ableitungen bildest? In diesem Artikel wird dir das ganze anschaulich mit Beispielen leicht verständlich erklärt. Am Ende findest du noch ein Quiz um das gelernte zu überprüfen.
Und los geht’s!
Stell dir vor, du hast eine Funktion, die aus der Summe von anderen Funktionen besteht. Du möchtest nun die Ableitung von dieser Funktion mit Summen bilden. Um es simpel zu halten, nehmen wir jetzt die Funktion f(x) = g(x) + h(x), und bilden davon die Ableitung:
In Worten ausgedrückt bedeutet das, um die Ableitung bilden zu können, müssen wir erst die einzelnen Teile g(x) und h(x) nach g´(x) und h´(x) ableiten. Wenn du das gemacht hast, kannst du alles addieren und hast die Ableitung deiner Funktion mit Summen gebildet.
Summenregel Rechenbeispiele
Damit du die Summenregel besser nachvollziehen kannst, folgen jetzt ein paar Beispiele.
Summenregel Beispiel 1
Für unser erstes Beispiel wollen wir die folgende Funktion f(x) ableiten:
Da hier zwei Funktionen addiert werden, nutzen wir die Regeln der Summenregel, die wir dir im Abschnitt zuvor erklärt haben. Unsere Funktion setzt sich aus g(x), links vom Pluszeichen und h(x), rechts vom Pluszeichen zusammen.
Jetzt leiten wir g(x) und h(x) nach g´(x) und h´(x) ab. Dafür nutzen wir die Regeln der Potenz- und der Faktorregel. Du nimmst also den Exponenten (bei g(x) die 2) und multiplizierst ihn mit unserem x. Danach reduzierst du den Exponenten um 1 (bei g(x) 2-1=1).
Nun können wir die beiden abgeleiteten Funktionen addieren und erhalten damit unsere Ableitung von f(x).

Summenregel Beispiel 2
Die Funktion f(x), die wir jetzt ableiten wollen, lautet:
Da auch diese Funktion eine Summe ist, benötigen wir die Summenregel zur Berechnung der Ableitung von f(x). Dafür teilen wir unsere Funktion wieder in die zwei Funktionen g(x), links vom Pluszeichen und h(x), rechts vom Pluszeichen auf.
Unsere zwei einzelnen Funktionen g(x) und h(x) können wir jetzt nach g´(x) und h´(x) ableiten. Du multiplizierst dafür bei g(x) den Exponenten -4 mit unserem -3x. Danach musst du den Exponenten um 1 reduzieren (hier: -4-1=-5).
Für h(x) machst du die gleichen Schritte. Du multiplizierst den Exponenten 5 mit den 6x und reduzierst im Anschluss den Exponenten um 1 (hier: 5-1=4).
Nun kannst du die beiden abgeleiteten Funktionen g´(x) und h´(x) addieren und erhältst damit die Ableitung f´(x) von unserer Funktion f(x).



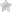 3,67 von 5 Sterne
3,67 von 5 Sterne
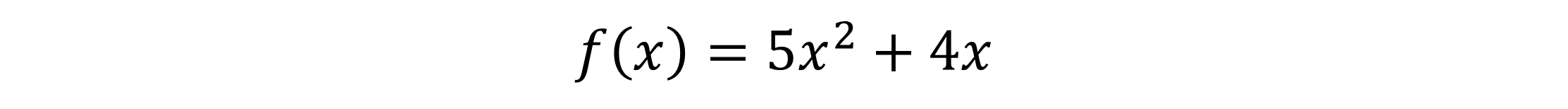
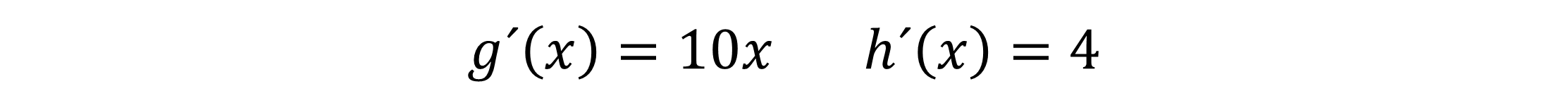
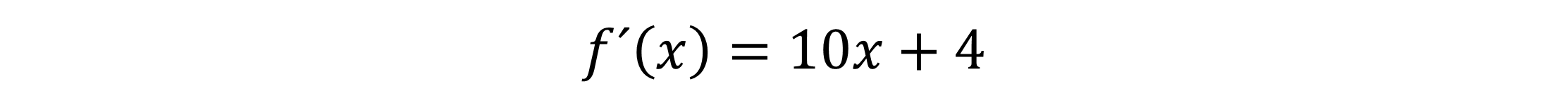
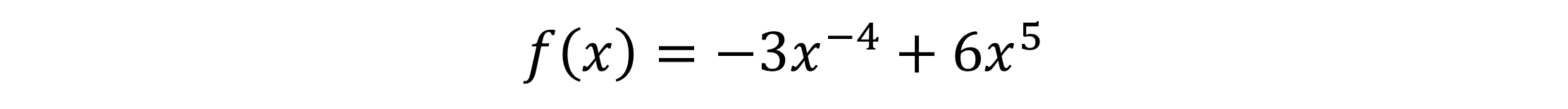
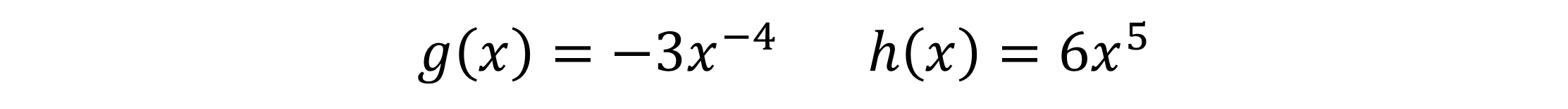

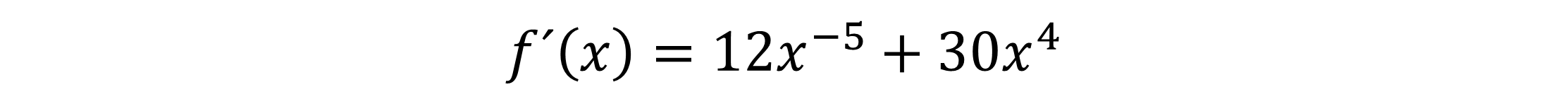



Super erklärt und einfach nachvollziehbar.
Toll gemacht