4,09 von 5 Sterne
Loading...
Was ist ein Steigungsdreieck und wie kann ich eins zeichnen? Das ist gar nicht so schwer.
Wir zeigen dir:
- wofür du ein Steigungsdreieck brauchst
- wie du die Steigung einer Geraden berechnest
- wie du in 5 Schritten ein Steigungsdreieck aufstellen kannst
- wie du ein Steigungsdreieck zeichnest
- wie du die Steigung einer Geraden auch ohne Steigungsdreieck einfach ablesen kannst
Steigungsdreieck – Wofür brauche ich das?
Ein Steigungsdreieck brauchst du, um (wie das Wort schon sagt) die Steigung einer Gerade zu bestimmen.
- Es gibt an, wie stark sich eine Funktion verändert.
- Dabei wird das Steigungsdreieck am häufigsten verwendet, um die Funktionsgleichung einer linearen Funktion zu bestimmen.
Wie berechnet man die Steigung?
Zuerst zeigen wir dir, wie du die Steigung bestimmen kannst, wenn du die Funktion einer Gerade bereits gegeben hast.
- b beschreibt den y-Achsenabschnitt. Das ist also der Punkt, an dem die lineare Funktion die y-Achse schneidet.
- m stellt die Steigung dar. Dadurch wird erklärt, wie flach oder steil eine Funktion verläuft. Wenn das m positiv ist, steigt die Funktion an und wenn das m negativ ist, fällt sie.
Hier sind ein paar Fragen, um zu überprüfen, ob du es verstanden hast!
Ergebnisse
Sehr gut gemacht!
Schade! Du musst noch ein bisschen üben.
#1. Welche Steigung hat die Funktion: y= 4x + 2?
#2. Welche Steigung hat die Funktion: y= 6x – 3?
#3. Welche Steigung hat die Funktion: y= -3x + 4?
#4. Welche Steigung hat die Funktion: y= -2x - 3?
Steigungsdreieck Formel
Um die Steigung berechnen zu können, musst du dir zwei Punkte auf der Geraden auswählen.
- Dabei ist es am einfachsten, wenn du zwei Punkte nimmst, die leicht ablesbar sind.
Die Formel für das Steigungsdreieck lautet:
m = \displaystyle \frac{y_2-y_1}{x_2-x_1} = \displaystyle \frac{Δy}{Δx}
Wir zeigen dir in einem Beispiel wie du diese Formel ganz leicht anwenden kannst.
Steigungsdreieck berechnen – Schritt für Schritt
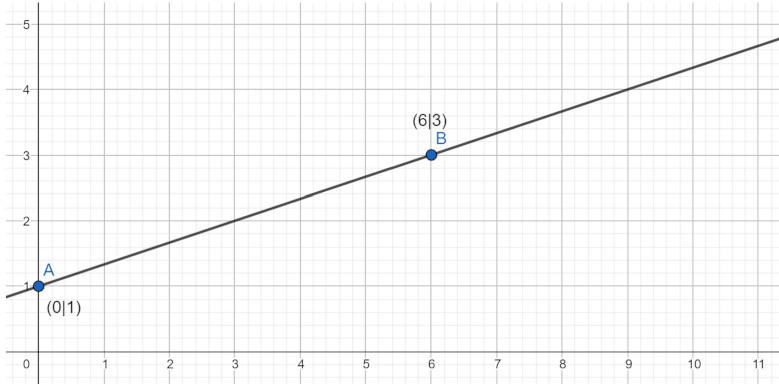
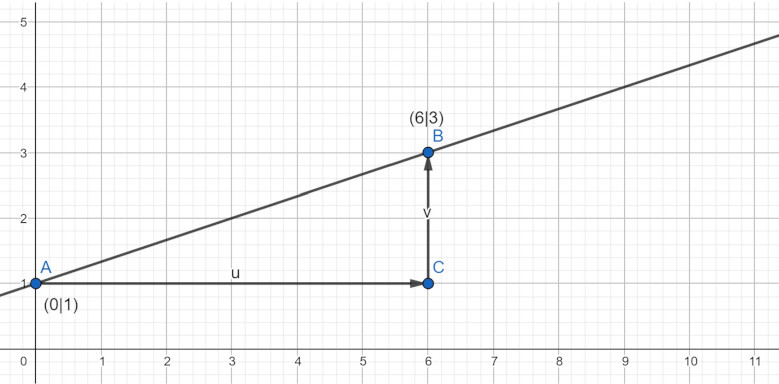
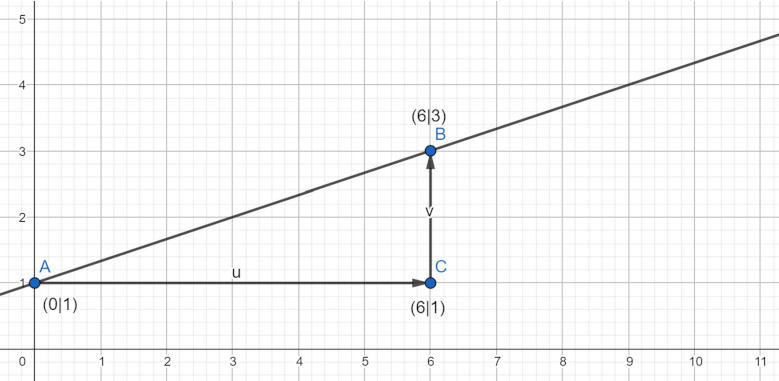
Zur Erinnerung Steigungsdreieck Formel:
Schritt 5
Jetzt setzen wir unsere Werte in die Formel ein. ∆y bedeutet die Änderung des y-Wertes.
- In unserem Fall sind wir 2 Schritte nach oben gegangen, also ist ∆y = 2. ∆x stellt die Änderung des x-Wertes dar.
- Hier sind wir 6 Schritte nach rechts gegangen als ist ∆x = 6.
- In die Formel eingesetzt ergibt das:
. - Somit hat die hier gegebene Funktion eine Steigung von
. - In die Formel lassen sich aber auch direkt die Koordinaten der Punkte A und B einsetzten.
- Dazu setzen wir die Punkte A (0|1) und B (6|3) in die Formel ein.
- Dabei erhalten wir das Ergebnis:
Du kannst also beide Formeln für die Berechnung der Steigung nutzen, je nachdem welche dir leichter fällt.
Funktion mittels Steigungsdreieck bestimmen
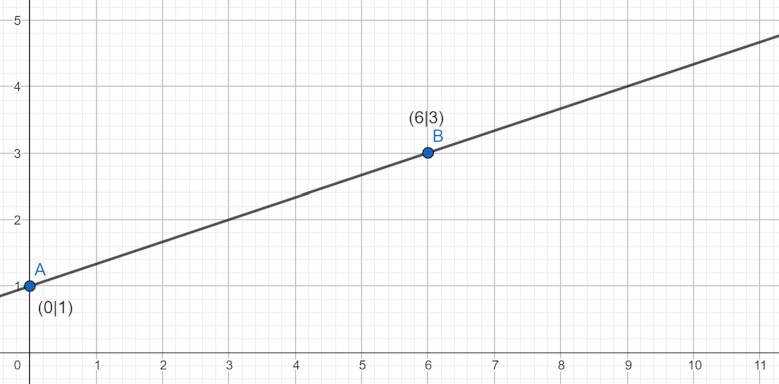
In einem letzten Schritt zeigen wir dir, wie du die Geradengleichung einer Funktion bestimmen kannst, wenn du diesen nur gezeichnet vor dir hast.
- In den Schritten 1 bis 5 haben wir die Steigung der Geraden also m bestimmt.
- Diesen Wert können wir in die Gleichung einsetzen
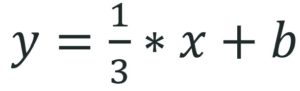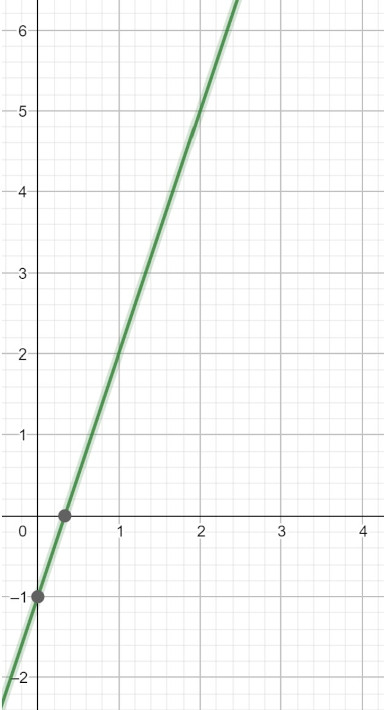
. - Jetzt fehlt nur noch der Wert für b. Diesen können wir aus der Zeichnung ablesen.
- Der Wert für b gibt den y-Achsenabschnitt, also den Schnittpunkt der Geraden mit der y-Achse an.
- In unserem Fall scheidet die Gerade die y-Achse bei y=1 und somit ist b=1.
- Wenn wir diesen Wert in die Geradengleichung einsetzen, haben wir diese auch schon komplett berechnet. Die Geradengleichung lautet:
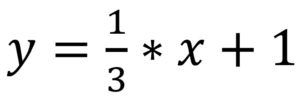
Steigungsdreieck Aufgaben
In diesen Aufgaben kannst du dein Wissen überprüfen und das Zeichnen von Steigungsdreiecken üben. Wenn du möchtest, kannst du auch die komplette Geradengleichung aufstellen und mit den Musterlösungen vergleichen.
Beachte, dass es immer mehrere Wege gibt, ein Steigungsdreieck zu zeichnen. Wichtig ist, dass du auf die gleiche Steigung wie in der Musterlösung kommst.
Berechne die Steigung der hier abgebildeten Geraden. Optional kannst du auch die komplette Funktionsgleichung bestimmen.
Steigung:
Geradengleichung:
Berechne die Steigung der hier abgebildeten Geraden. Optional kannst du auch die komplette Funktionsgleichung bestimmen.
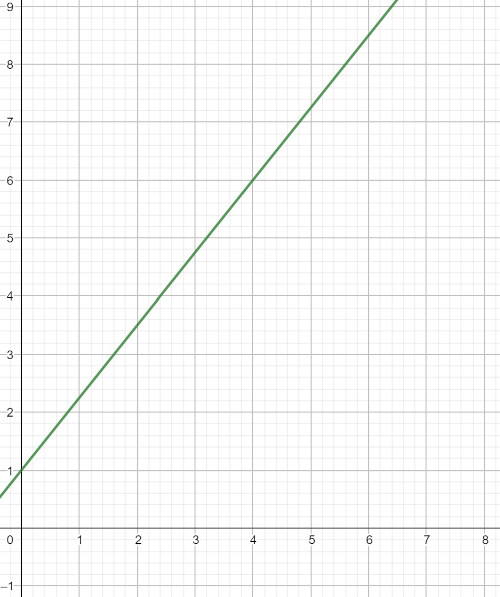
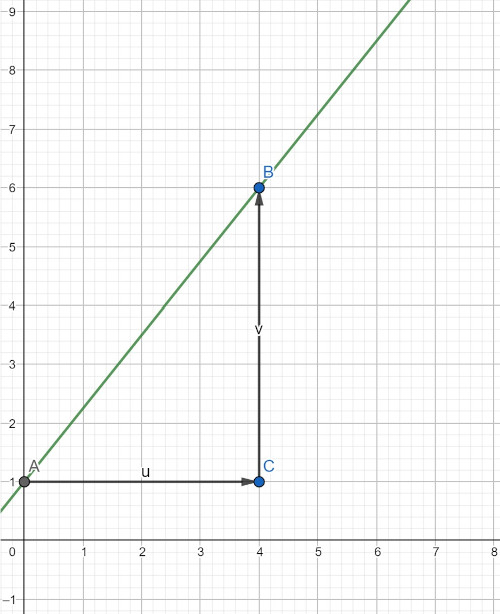
Steigung:
Geradengleichung:
Berechne die Steigung der hier abgebildeten Geraden. Optional kannst du auch die komplette Funktionsgleichung bestimmen.
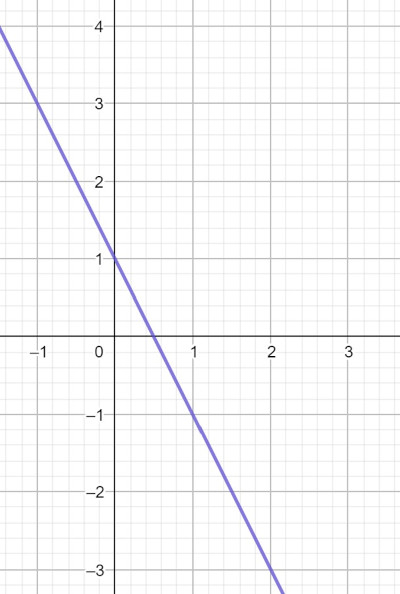
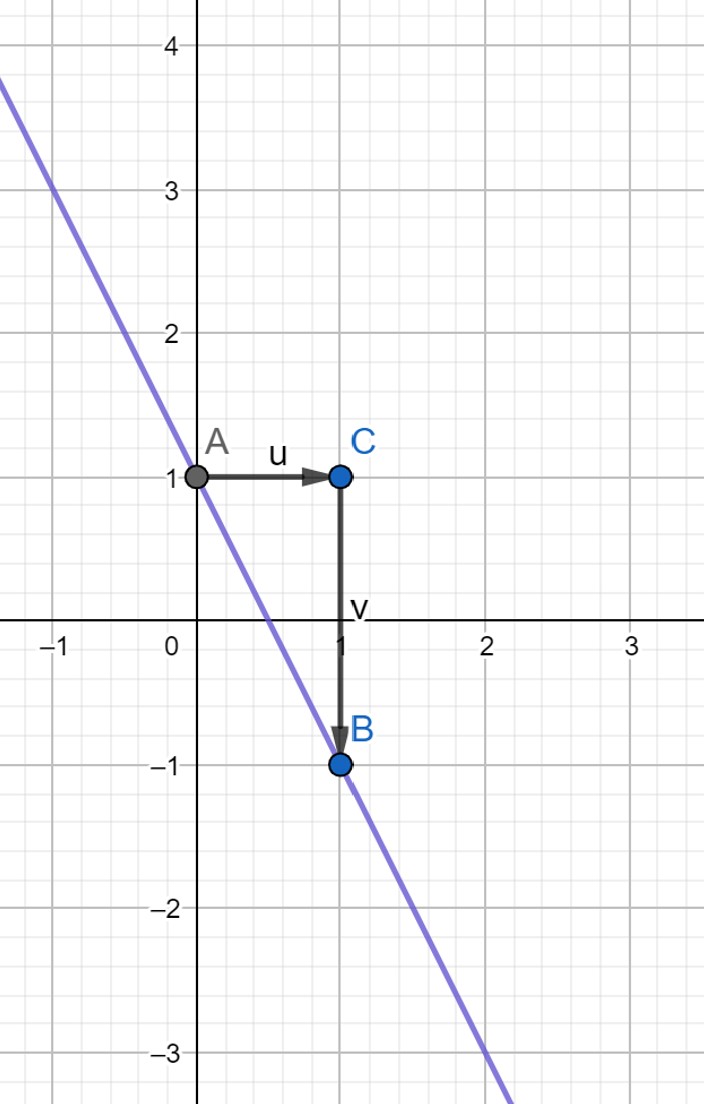
Steigung:
Geradengleichung:
Berechne die Steigung der hier abgebildeten Geraden. Optional kannst du auch die komplette Funktionsgleichung bestimmen.
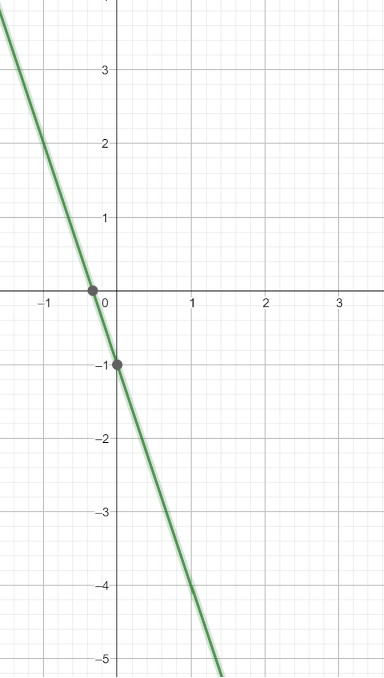
Steigung:
Geradengleichung:
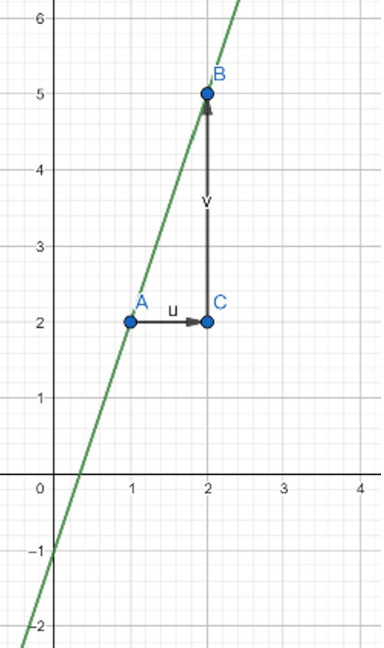
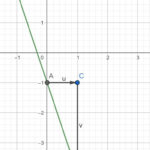
Die 5 Schritte im Überblick:
- Zwei Punkte auf der Geraden Aussuchen
- Den Punkt C einzeichnen: horizontaler und vertikaler Abstand zwischen den Punkten A und B
- Steigungsdreieck zwischen den Punkten ABC zeichnen
- Den horizontalen und vertikalen Abstand zwischen den Punkten berechnen
- In die Formel für die Steigung den horizontalen und vertikalen Abstand zwischen den Punkten einsetzen
FAQ zu Steigungsdreieck
Wie berechnet man ein Steigungsdreieck?
Um ein Steigungsdreieck zu berechnen, musst du nacheinander folgende Schritte durchgehen:
- Zwei gut ablesbare Punkte auf der gegebenen Geraden aussuchen (Punkte A und B)
- Ausgehend von dem Punkt A läufst du waagerecht nach rechts und von Punkt B aus senkrecht nach unten
- Rechtwinkliges Steigungsdreieck zeichnen
- Deine berechneten Punkte in die Formel für das Steigungsdreieck einsetzen
Wie lautet die Formel für das Steigungsdreieck?
Die Formel lautet: m = \displaystyle \frac{y_2-y_1}{x_2-x_1} = \displaystyle \frac{Δy}{Δx}
Wie kann man die Geradengleichung einer linearen Funktion bestimmen?
Um die Geradengleichung zu bestimmen, rechnen wir zuerst die Steigung der Geraden mit Hilfe des Steigungsdreiecks aus. Danach lesen wir den y-Achsenabschnitt anhand der Zeichnung ab. Dazu lesen wir ab, wann die Gerade die y-Achse schneidet. Diesen Punkt setzen wie in die Geradengleichung der Form y=m*x + b für das b ein.
Kennst du schon unsere Artikel zu Umkehrfunktionen und Maßeinheiten? Klick dich mal durch.
Hinterlass eine Bewertung...
…das wäre wirklich super nett! Damit tust du uns einen riesen Gefallen! 🙂
4,09 von 5 SterneLoading...
Alles sehr schön dargestellt und bis auf die Formeln (für mich!) nachvollziehbar. Leider weiß ich noch immer nicht, wozu man das einsetzen kann, also im sogenannten wirklichen leben, wie etwa die Bestimmung eines Rechten Winkels auf freiem feld nach Pytagoras und der Formel 3 – 4- 5
Herzlichen Dank!