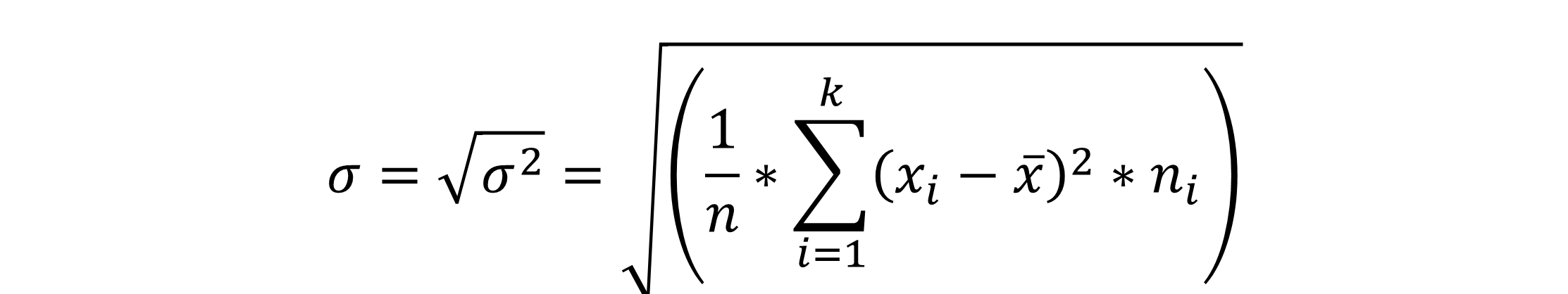In diesem Artikel erfährst du, was die Standardabweichung ist. Wie du sie berechnen und interpretieren kannst. Was der Zusammenhang zwischen ihr und der Varianz ist.
Das ganze einfach nachvollziehbar mit Beispielen erklärt. Zum Abschluss noch ein Quiz, damit du dein Wissen abfragen kannst.
Komm schauen wir uns das ganze mal an!
Die Standardabweichung ist ein lineares Streumaß. Sie beschreibt die durchschnittliche Entfernung vom arithmetischen Mittel (Durchschnitt). Mit anderen Worten: Die Standardabweichung ist die durchschnittliche Abweichung aller Merkmalsausprägungen vom Mittelwert.
Standardabweichung Berechnen
Du kannst die Standardabweichung berechnen, indem du die Quadratwurzel der Varianz bildest. Hast du statt der Varianz nur die Stichprobenwerte gegeben, zeigen wir dir in einfachen Schritten an Hand eines Beispiels, wie du die Standardabweichung berechnen kannst.
Standardabweichung und Varianz – Zusammenhang
Wie bereits gerade erklärt, kannst du die Standardabweichung berechnen, indem du die Quadratwurzel aus der Varianz bildest. Andersherum kannst du bei gegebener Standardabweichung die Varianz berechnen, indem du den Wert quadrierst (hoch 2 rechnest).
Die Varianz beschreibt die mittlere quadratische Abweichung um den Mittelwert. Du kannst sie mit den folgenden Formeln berechnen:
Varianz für Einzeldaten:
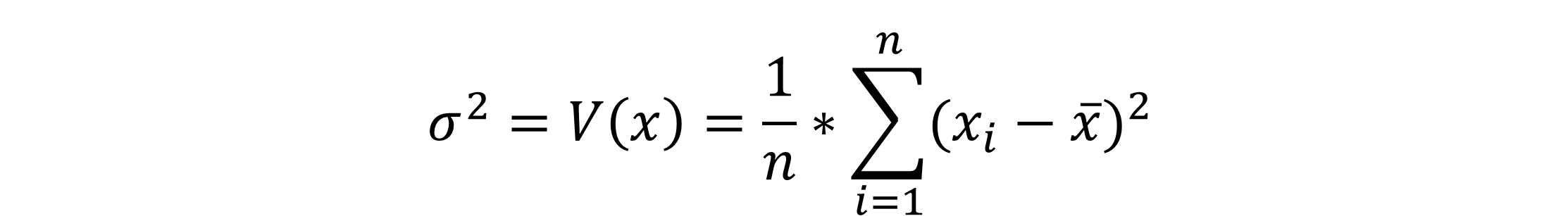 Du kannst die Varianz für Einzeldaten berechnen, indem du die Differenzen der Einzelwerte von X und des Mittelwertes bildest und quadrierst diese, um keine negativen Werte zu erhalten.
Du kannst die Varianz für Einzeldaten berechnen, indem du die Differenzen der Einzelwerte von X und des Mittelwertes bildest und quadrierst diese, um keine negativen Werte zu erhalten.
Dann addierst du alle Ergebnisse zusammen und teilst durch die Anzahl aller Merkmalausprägungen.
Varianz für klassierte Daten:
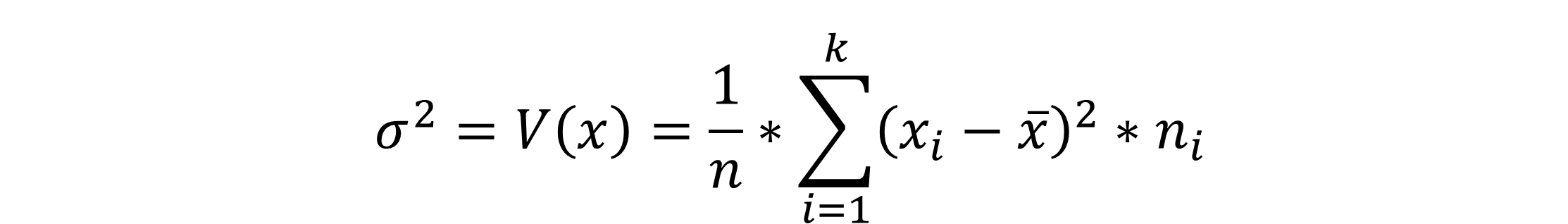 Du kannst die Varianz für klassierte Daten berechnen, indem du die Differenzen der Einzelwerte von X und des Mittelwertes bildest und quadrierst diese, um keine negativen Werte zu erhalten.
Du kannst die Varianz für klassierte Daten berechnen, indem du die Differenzen der Einzelwerte von X und des Mittelwertes bildest und quadrierst diese, um keine negativen Werte zu erhalten.
Dann gewichtest du die einzelnen Ergebnisse mit ihren individuellen Häufigkeiten für die jeweilige Klasse (k). Abschließend addierst du alle Ergebnisse zusammen und teilst durch die Anzahl aller Merkmalausprägungen.
Standardabweichung Formel
So, da nun weißt, wie die Varianz und die Standardabweichung im Zusammenhang stehen, zeigen wir dir jetzt die Formel:
Wie du siehst, brauchst du dir nur merken: Zum berechnen der Standardabweichung, die Quadratwurzel aus der jeweiligen Varianz bilden!
Beispiel – Standardabweichung Berechnen

Stell dir vor, in deiner Klasse wurde eine schwierige Mathearbeit geschrieben. Euer Lehrer schreibt dir folgende Notenverteilung an die Tafel.
Note: | 1 | 2 | 3 | 4 | 5 | 6 |
Anzahl: | / | 8 | 15 | 6 | 1 | / |
Du möchtest nun die Standardabweichung für eure Klassenarbeit berechnen!
Das Arithmetisches Mittel berechnen:
Dafür multiplizieren wir die Note mit der jeweiligen Häufigkeit (Anzahl) und teilst durch die Gesamtanzahl an Schülern (30).
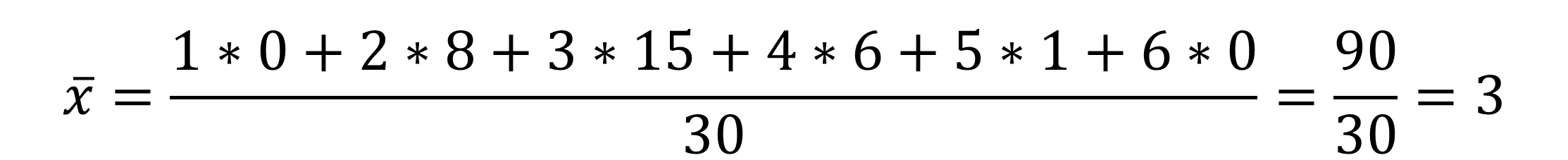
Der Notendurchschnitt deiner Klasse ist die Note drei.
Die Varianz berechnen:
Wir können jetzt unsere Formel für klassierte Daten nehmen, da die sechs Schulnoten als Klassen/Gruppen fungieren. Den Mittelwert und den Wert für die Gesamtanzahl können wir in die Formel einsetzen:
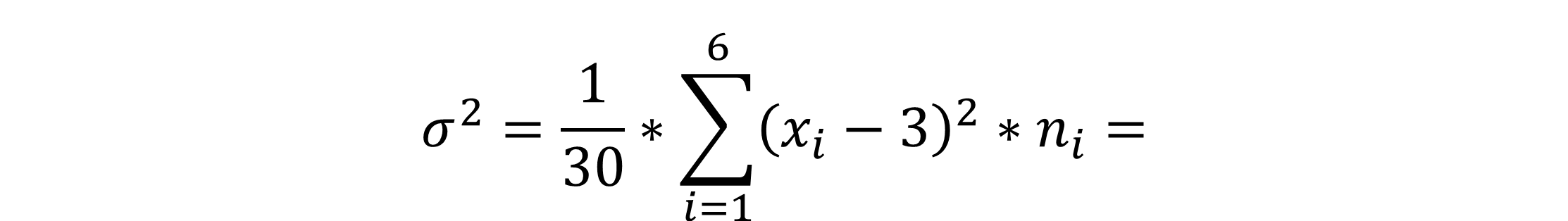
Wenn du das ganze ausschreibst, dann subtrahierst du von jeder Note den Mittelwert (3). Das Ergebnis dieser Subtraktionen quadrierst du jeweils und multiplizierst diesen Wert wiederum mit der Häufigkeit für die jeweilige Note.
Die Ergebnisse dieser Berechnungen addierst du zusammen und teilst alles durch die Gesamtanzahl an Klassenarbeiten (30).
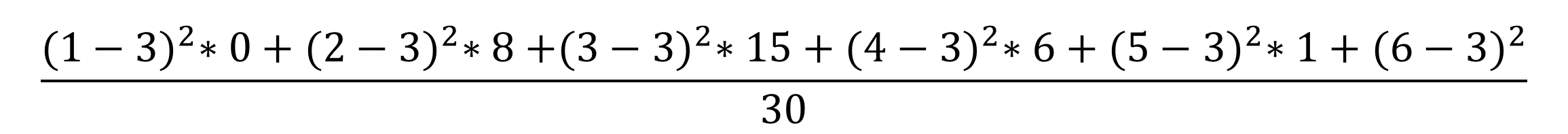
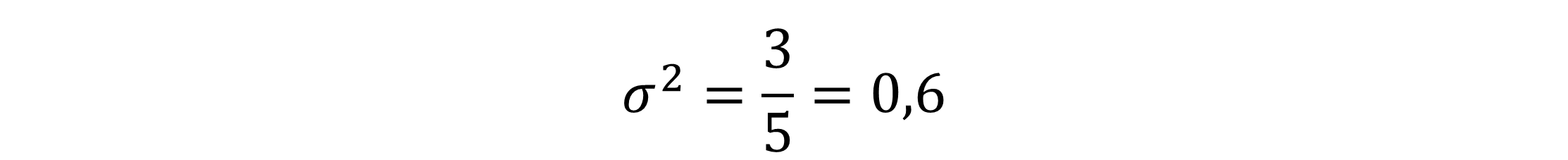
Unsere Varianz beträgt somit 0,6 Noten2.
Die Standardabweichung berechnen:
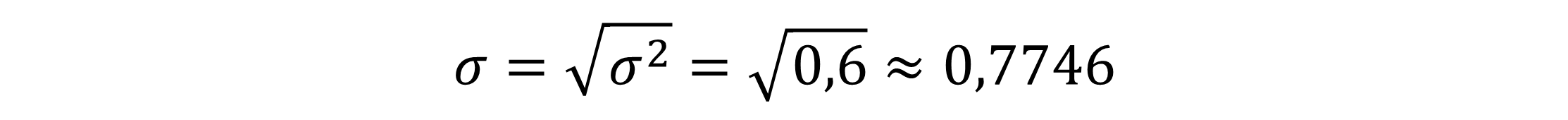
Um unsere Standardabweichung zu berechnen, müssen wir jetzt nur noch die Quadratwurzel von unserer Varianz bilden. Unsere Standardabweichung beträgt ungefähr 0,7746.
Standardabweichung Interpretation:
Die Standardabweichung lässt sich als die durchschnittliche Abweichung vom arithmetischen Mittel (Mittelwert) interpretieren.
Für unser Beispiel mit den Noten der Mathearbeit bedeutet das, dass die Noten der Schüler im Durchschnitt um ungefähr 0,7746 Noten vom Mittelwert (3) abweichen.
Standardabweichung Rechner

Abschließend noch ein Tipp:
Wenn dir mal die Zeit/Lust fehlt oder du nicht weiterkommst. Hier ein Online-Rechner für die Standardabweichung. Dort kannst du deine Zahlen eingeben und schnell ein ausführliches Ergebnis erhalten. 😊

 4,60 von 5 Sterne
4,60 von 5 Sterne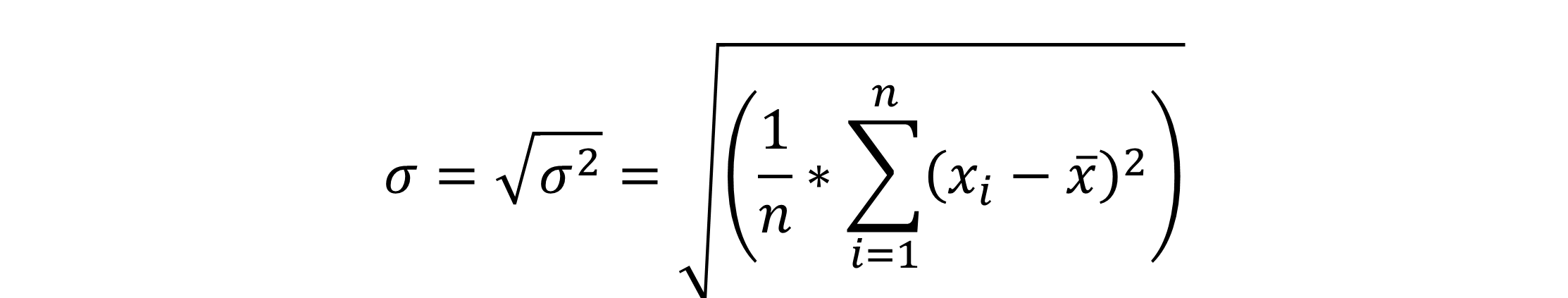 Formel für klassierte Daten:
Formel für klassierte Daten: