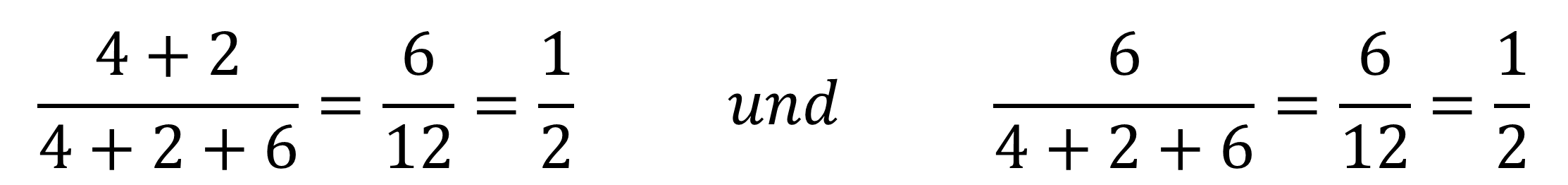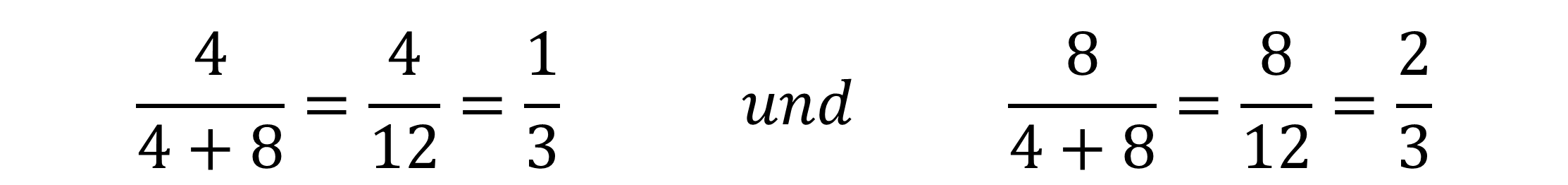Die Spieltheorie – Einfach erklärt mit Beispielen

In diesem Artikel erfährst du, was Spieltheorien sind, welche es gibt und wie du sie unterscheiden kannst. Außerdem was ein Nash-Gleichgewicht ist und wie du es für verschiedene Spiele bestimmen kannst.

Das ganze einfach nachvollziehbar mit Beispielen erklärt. Zum Abschluss noch ein Quiz, damit du dein Wissen abfragen kannst.

Lasst uns beginnen!

Definition – Was sind Spieltheorien?

Die Spieltheorie der VWL ist ein Zweig der Gesellschaftswissenschaften, der zur formalen Analyse der strategischen Entscheidungen von beispielsweise Unternehmen genutzt wird.

Dabei sind die verschiedenen Spieler nicht unabhängig, denn die Auszahlung an einen Spieler hängt von den Entscheidungen, bzw. dem Verhalten der anderen Spieler ab. Die Darstellung von verschiedenen Verhaltensalternativen und Auszahlungen findet in den Auszahlungsmatrizen statt.

Das Ziel des ganzen ist es, den Ausgang eines Spiels voraussagen zu können und zum Beispiel Tipps für zukünftiges Handeln geben zu können.

Elemente eines Spiels

Ein Spiel hat immer die 4 Elemente (PAPI) Players (Spieler), Actions (Aktionen), Payoffs (Auszahlungen) und Information (Informationen), die die Unterschiede der verschiedenen Spiele ausmachen:

Des Weiteren lassen sich die verschiedenen Spiele noch in den folgenden Punkten unterscheiden:

Nash-Gleichgewicht – Spieltheorie

Ein Nash-Gleichgewicht ist das Ergebnis eines (nicht kooperativen) Spiels, bei dem die wechselseitig verbundenen Spieler ihre bestmögliche Strategie (d.h. maximale Auszahlung) mit Blick auf die Entscheidung (Strategie) der anderen Spieler und ohne Rücksicht auf deren Auszahlung treffen.

Es handelt sich um ein Gleichgewicht, weil keiner der Spieler einen Anreiz besitzt, seine Strategie zu ändern. Gegeben sind dabei die bestmöglichen Strategien der anderen Spieler.

Welche Darstellungsformen in der Spieltheorie gibt es?

Mit Hilfe der Punkte aus dem Elemente Abschnitt kannst du dem Spiel eine grafische Darstellung zuordnen, am häufigsten in Form einer Matrix. Durch die grafische Darstellung ist es beispielsweise einfach für dich, das Nash-Gleichgewicht herauszufinden.

Die Normalform

In der Normalform eines Spiels findet die Wahl der Strategie simultan (gleichzeitig) und ohne Kenntnis der anderen Spieler statt. Deshalb eignet sich hierfür meistens die Darstellung des Spieles mit einer Bimatrix.

Weiter hinten im Text kommen spezifische Beispiele für Normalformen des Spiels, bei denen wir das Nash-Gleichgewicht berechnen.

Die Extensivform

Die alternative Spielform dazu ist eine extensive Spielform, bei der es sich um ein sequentielles Spiel handelt.

Da bei diesem Spiel die Entscheidungen nacheinander getroffen werden und dementsprechend den Spielern mehr Informationen zur Verfügung stehen, ist hier die Darstellung durch einen Spielbaum sinnvoll, um Reihenfolge und Auszahlung sichtbar zu machen.

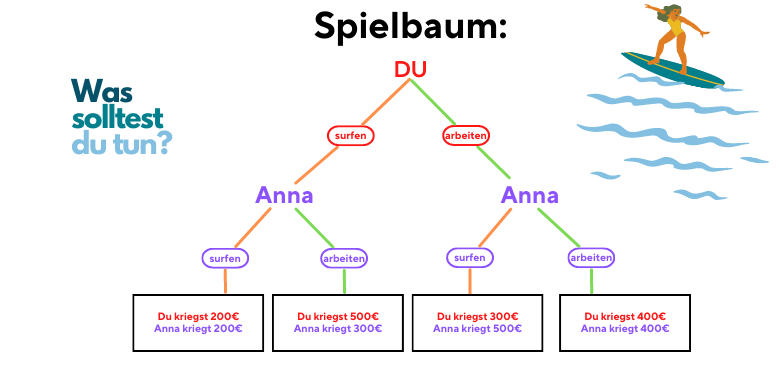
Damit du das ganze besser nachvollziehen kannst hier ein Beispiel Spielbaum:

Anna und du arbeiten in einem Surfshop am Meer. Du triffst zuerst eine Entscheidung, ob du heute arbeitest oder ob du surfen gehst.

Anna hat Information darüber, für welche Option du dich entschieden hast, und wählt danach zwischen den beiden Möglichkeiten.

Euch Beiden sind die Payoffs (Auszahlungen), die ihr, je nachdem wie gewählt wird, bekommt, bekannt.

Um unser Beispiel zu lösen, schauen wir uns die zwei möglichen rationalen Strategien von Anna an.

Wenn du dich für das Arbeiten entscheidest, wird Anna surfen, da sie dann 500€ bekommen würde, was mehr ist als 400€, wenn beide von euch arbeiten würden. Dein Payoff bei diesem Endknoten wären 300€.

Würdest du dich jedoch für Surfen entscheiden, wäre die bestmögliche Auszahlung für Anna 300€, wenn sie sich für das Arbeiten entscheiden würde, da dies mehr ist als die 200€, die sie bekommen würde, wenn sie auch surfen gehen würde. In diesem Fall würdest du 500€ bekommen.

So, da du nun weißt, welche beiden Entscheidungen Anna als Resultat deiner Entscheidung treffen würde, was wäre für dich am besten? Was solltest du tun?

Spieltheorie in der VWL

Die Spieltheorie spielt eine große Rolle in der Volkswirtschaftslehre und wird genutzt, um das wirtschaftliche Verhalten der Spieler (Unternehmen) und deren Reaktion auf die Strategie der anderen darzustellen. Dabei wird insbesondere das Nash-Gleichgewicht für den Bertrand- bzw. Cournot-Wettbewerb bestimmt.

Des Weiteren sind klassische Beispiele der Spieltheorie die zum Einsatz kommen, das Gefangenendilemma, das Battle of the Sexes (Kampf der Geschlechter) und das Feiglingsspiel (Chicken Game). Auf diese drei Beispiele gehen wir jetzt noch einmal genau ein und bestimmen jeweils das Nash-Gleichgewicht mit Erklärung.

Das Gefangenendilemma in der Spieltheorie

Um dir das ganze anschaulich darzustellen, nutzen wir direkt ein Beispiel.

Stell dir vor, du und deine Freundin Gina haben einen Raub begangen. Die Polizei hat euch auf frischer Tat ertappt und mit auf die Wache genommen. Dort haben sie euch getrennt. Es kommt zum gleichzeitigen Verhör in zwei unterschiedlichen Räumen, bei dem ihr nicht wisst, was der andere macht.

Es wird euch beiden vom leitenden Kommissar ein Deal angeboten. Ihr könnt zugeben, eine Waffe mit am Tatort gehabt zu haben (Wäre bewaffneter Raub, was eine höhere Strafe hätte). Zusätzlich gibt er euch eine Matrix. Auf dieser stehen die Zahlen für die Jahre im Gefängnis. Wie solltest du dich entscheiden?

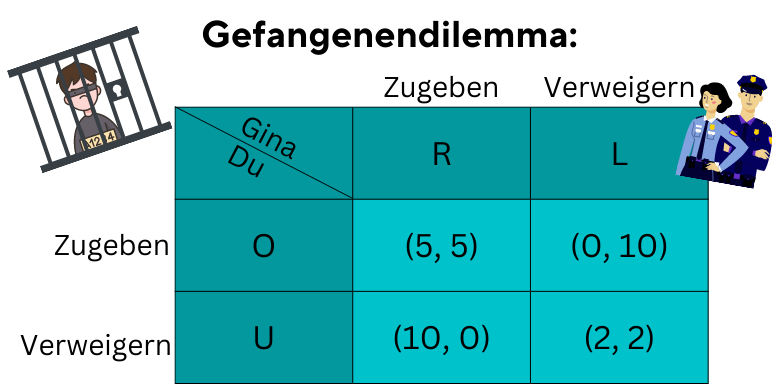
Wenn nur einer von euch beiden den Deal verweigert und der andere zugibt, dann kommt der, der die Waffe zugibt, in Freiheit. Der andere bekommt 10 Jahre Strafe.

Wenn beide von euch zugeben würden, teilt ihr die 10 Jahre Strafe zwischen euch auf und jeder kriegt 5 Jahre.

Würdet ihr euch jeweils für das Verweigern der Aussage entscheiden, dann würdet ihr 2 Jahre in Haft nur für den Raub bekommen.

Nash-Gleichgewicht bestimmen

Um nun das Nash-Gleichgewicht zu bestimmen, müssen wir erst einmal gucken, was die dominante Strategie ist. Du musst jetzt überlegen, wie Gina sich entscheidet.

Wenn du denkst, das sie die Aussage verweigert, dann solltest du dich fürs Zugeben entscheiden. Du kommst dann frei und sie bekommt 10 Jahre. Gehst du jedoch davon aus, dass sie zugibt, eine Waffe am Tatort gehabt zu haben, solltest du auch zugeben. So würdest du nämlich 5 Jahre Freiheitsstrafe bekommen, was besser ist als 10 Jahre fürs Verweigern der Aussage.

Somit siehst du, egal was du denkst, wie Gina sich entscheidet, du wirst immer zugeben wählen (dominante Strategie). Für Gina laufen die Entscheidungen, die sie trifft genau gleich ab und auch sie wird sich immer für Zugeben entscheiden.

Damit ist das Nash-Gleichgewicht für dieses Spiel (Zugeben, Zugeben)/(Oben/Rechts).

Und deshalb handelt es sich bei diesem Spiel um ein Dilemma, da die Gefangenen sich immer für Zugeben entscheiden werden. Das ist im Ganzen betrachtet schlechter, als wenn beide kollektiv die Aussage verweigern würden und nur jeweils 2 Jahre kriegen würden.

Battle of the Sexes

Auch das “Kampf der Geschlechter”-Spiel erklären wir dir mit einem Beispiel.

Stell dir vor, ein Mann und eine Frau möchten gemeinsam den Abend verbringen. Es gibt zwei Möglichkeiten an zwei verschiedenen Orten. Die beiden haben aber vergessen, sich vorher zu einigen und müssen jetzt jeweils voneinander unabhängig eine Entscheidung treffen.

Der Mann präferiert das Fußballspiel, die Frau den Theaterbesuch.

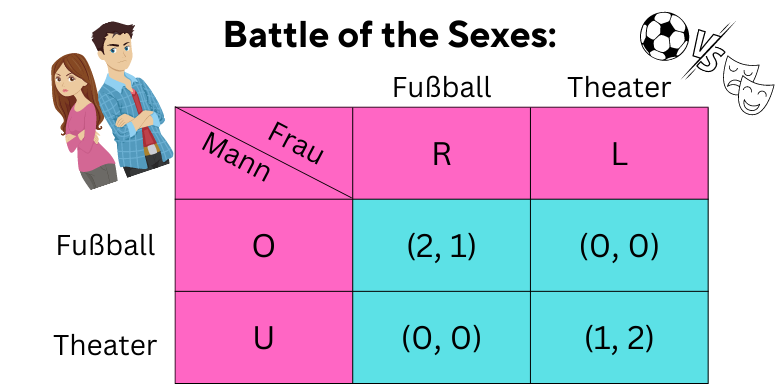
Würde sich der Mann entscheiden, zum Fußball zu gehen, wäre das auch die beste Entscheidung für die Frau. Das gleiche gilt umgekehrt für den Theaterbesuch. Somit gibt es für dieses Spiel zwei Nash-Gleichgewichte, (Fußball, Fußball) und (Theater, Theater).

Bei diesem Spiel gibt es keine dominante Strategie. Wenn sich beide Spieler für Ihre jeweilige Präferenz entscheiden würden, würden sie sich nicht treffen.

Das Hauptziel beider ist es, den Abend an einem gemeinsamen Ort zusammen zu verbringen. Entscheiden sich beide wiederum so und wählen die Präferenz des anderen, nur um zusammen zu sein, wären sie wieder nicht am gleichen Ort.

Spieltheorie Chicken Game – Feiglingsspiel

Ebenfalls dieses Spiel wollen wir dir mit einem Beispiel nahe bringen.

Stell dir vor, zwei junge Adrenalin suchende Männer, Tom und Max wollen eine Mutprobe mit ihren Autos machen. Die beiden fahren aufeinander zu. Wer nicht ausweicht, gewinnt die Mutprobe. Derjenige, der ausweicht, ist ein “Chicken” oder Feigling.

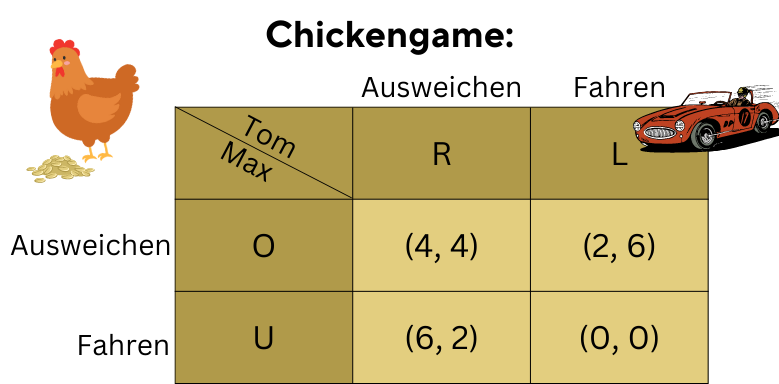
Sowohl Tom, als auch Max gewinnen, wenn der andere ein “Feigling” ist und ausweicht, während sie kaltblütig weiterfahren (6, 2). Entscheiden sich beide für ausweichen, gewinnt zwar keiner die Mutprobe, aber beide überleben. Der Nutzen für beide ist dann 4.

Weichen beide nicht aus, gewinnen beide die Mutprobe, bezahlen jedoch mit ihrem Leben. Deshalb ist der Nutzen für diesen Fall 0.

Für reine Strategien gibt es zwei Nash-Gleichgewichte: (ausweichen, fahren) und (fahren, ausweichen). Da der individuell bestmögliche Nutzen bei 6 liegt.

Haben wir eine gemischte Strategie, gibt es nur ein Nash-Gleichgewicht. Hier hängt das Gleichgewicht von den exakten Werten in der Auszahlungsmatrix ab. Für unser Beispiel liegt die Wahrscheinlichkeit, dass Max und Tom ausweichen oder weiterfahren, bei jeweils 1/2.

Hätten wir jedoch einen höheren Nutzen für eine Sieg, z.B. 8 statt 6 und einen Nutzen von 0 statt 2 , dann würde das Nash-Gleichgewicht ganz anders aussehen. Hierfür wäre es (1/3, 2/3); (1/3, 2/3) statt (1/2, 1/2); (1/2, 1/2).

Abschlussquiz: