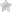3,67 von 5 Sterne
Loading...
Der Satz des Thales kann dir im Matheunterricht sehr nützlich sein, besonders wenn du dich gerade mit Trigonometrie beschäftigst.
Deshalb lernst du hier…
- …was der Satz des Thales ist
- …wie man einen Thaleskreis konstruiert
- …wie man den Satz des Thales umkehrt und beweist
Am Ende kannst du dein Wissen mit einem Quiz überprüfen.
Worauf wartest du noch?
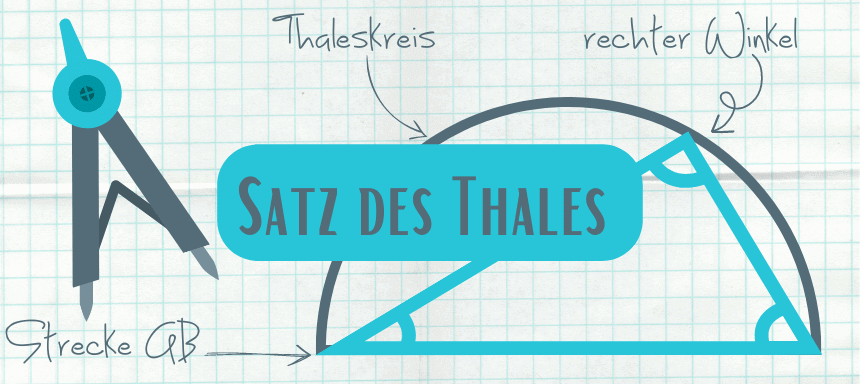
Der Satz des Thales ist ein wichtiger Satz der Mathematik. Benannt ist er nach dem griechischen Naturwissenschaftler und Philosophen Thales von Milet.
Bevor du lernst, wie man den Satz des Thales anwendet, werden hier ein paar grundlegende Fragen beantwortet.
Wie lautet der Satz des Thales?
Der Satz des Thales besagt:
Ein Dreieck aus den Endpunkten des Durchmessers (A und B) eines Halbkreises und einem beliebigen Punkt C auf dem Halbkreisbogen ist immer rechtwinklig.
Dabei ist der Punkt auf dem Halbkreis, der mit einem 90° Winkel.
Ein rechter Winkel hat immer 90°!
Es ist egal, welchen Punkt C man wählt, alle Winkel auf dem Halbkreis haben 90°.
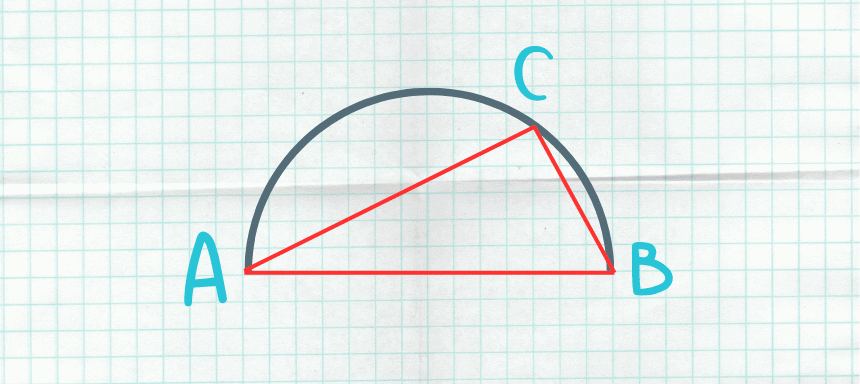
Das heißt umgekehrt: Liegt der Punkt C nicht auf dem Halbkreisbogen hat das Dreieck keinen 90° Winkel und ist somit nicht rechtwinklig.
Der Halbkreisbogen wird auch Thaleskreis genannt.
Was macht man mit dem Satz des Thales?
Der Satz des Thales sagt aus, wann ein Dreieck einen 90° Winkel hat. Er kann dir dabei helfen, ein rechtwinkliges Dreieck ohne Geodreieck zu zeichnen.
Man kann damit auch überprüfen, ob es sich um ein rechtwinkliges Dreieck handelt.
Den Thaleskreis anwenden – Schritt für Schritt
Nachdem du nun weißt, wozu man den Satz des Thales braucht, zeigen wir dir jetzt, wie man ihn konstruiert und umkehrt.
Wie konstruiert man den Satz des Thales?
Um den Satz des Thales anzuwenden, musst du einen Thaleskreis zeichnen. Das geht in wenigen einfachen Schritten.
Schritt 1: Eine Strecke zeichnen
Als Erstes zeichnest du eine beliebig lange Strecke mit dem Startpunkt A und Endpunkt B. Achte darauf, dass du sie nicht zu lang machst, damit du später keine Platzprobleme bekommst.
Diese Strecke stellt später die Hypotenuse des Dreiecks dar.
Schritt 2: Den Mittelpunkt der Strecke bestimmen
Bestimme nun mithilfe des Lineals den Mittelpunkt der Strecke und markiere ihn.
Schritt 3: Einen Halbkreis zeichnen
Setze nun den Zirkel mit der Metallspitze am Mittelpunkt M und der Zeichenseite an einem Endpunkt der Strecke (Punkt A oder B) an. Zeichne mit dem Zirkel einen Halbkreis, der die Punkte A und B verbindet.
Die Strecke zwischen A und B ist nun der Durchmesser des Halbkreisbogen.
Schritt 4: Einen Punkt C wählen
Jetzt kannst du dir einen beliebigen Punkt auf dem Halbkreis aussuchen und markieren. Dieser Punkt ist der Punkt C.
Schritt 5: Die Punkte zu einem Dreieck verbinden
Verbinde die drei Punkte A, B und C zu einem Dreieck. Damit bist du auch schon fertig mit der Konstruktion des Satz des Thales.
Schritt 6: Die Zeichnung überprüfen
Zum Schluss kannst du mithilfe eines Geodreiecks überprüfen, ob deine Zeichnung richtig ist. Hat der Punkt C auf dem Halbkreis 90°, hast du alles richtig gemacht. Das Dreieck ist rechtwinklig.
Wie lautet die Umkehrung des Satz des Thales?
Kann man das Dreieck so über den Kreis legen, dass alle drei Punkte (A,B,C) den Kreis berühren und die Hypotenuse des Dreiecks gleich dem Durchmesser des Kreises ist, ist das Dreieck rechtwinklig. Der Mittelpunkt des Kreises ist dann gleich dem Mittelpunkt der Hypotenuse.
Der rechte Winkel des Dreiecks liegt auch hier gegenüber der Hypotenuse auf dem Kreisbogen.
So kann man überprüfen, ob ein Dreieck einen 90° Winkel hat.
Dies ist nicht der Fall wenn:
- Sich die Hypotenuse des Dreiecks nicht mit dem Durchmesser des Kreises deckt.
- Sich der Mittelpunkt der Hypotenuse sich nicht mit dem Mittelpunkt des Kreises deckt.
- Einer der Punkte nicht auf dem Kreis liegt.
Den Satz des Thales beweisen – so wird es gemacht
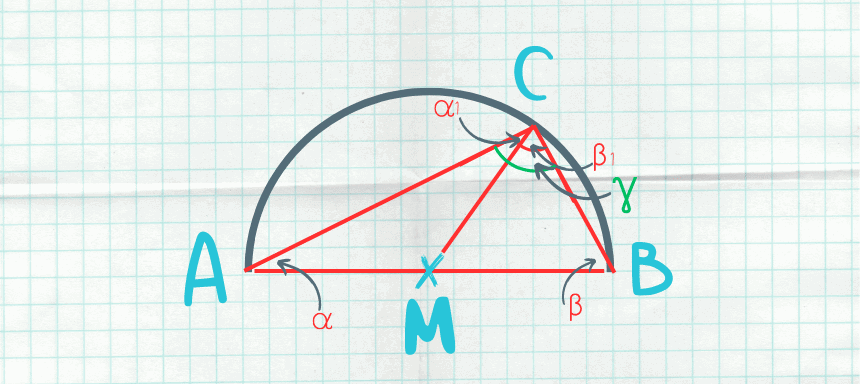
Um zu beweisen, dass der Satz des Thales gilt, muss man lediglich eine Seitenhalbierende zwischen den Punkten C und M in das Dreieck einzeichnen.
Dadurch entstehen neben dem Dreieck ABC noch zwei weitere Dreiecke. Die Dreiecke ACM und BCM. Diese zwei Dreiecke sind gleichschenklig.
Bei einem gleichschenkligen Dreieck sind zwei Seiten gleich lang und zwei Winkel sind identisch.
In unserem Fall sind jeweils die Winkel ɑ und ɑ1 und die Winkel ꞵ und ꞵ1 gleich groß.
Die Summe der Winkel ɑ1 und ꞵ1 entspricht dabei dem Winkel ɣ des Dreiecks ABC.
Der Innenwinkelsummensatz besagt, dass die Summe aller Winkel eines Dreiecks 180° beträgt.
Nach dem Innenwinkelsummensatz ergeben sich folgende Gleichungen:
Da ɑ=ɑ1 und β=β1, kann man in der zweiten Gleichung ɑ durch ɑ1 und β durch β1 ersetzen. Somit ergibt sich folgende Gleichung:
Diese Gleichung lässt sich zusammenfassen zu:
Dies lässt sich durch zwei teilen zu:
Da die Summe von ɑ1 und β1 gleich dem Winkel ɣ ist, ist ɣ ebenfalls gleich 90°.
Somit ist der Winkel ɣ ein rechter Winkel und das Dreieck ein rechtwinkliges Dreieck, egal wo der Punkt C auf dem Halbkreis liegt.
Fragen mit Lösungen – zum Üben und Vertiefen
Als Übung kannst du versuchen selbst einen Thaleskreis zu zeichnen. Dazu kannst du einfach den oben gezeigten Schritten folgen.
Gelingt dir dies, versuche auch den Beweis zeichnerisch durchzuführen. Damit kannst du überprüfen, ob dir der Thaleskreis gelungen ist.
Sind die zwei Dreiecke nicht gleichschenklig, ist dir irgendwo ein Fehler unterlaufen. Aber keine Panik! Versuche es einfach nochmal – es gelingt dir bestimmt.
Das Grundlagenwissen, dass du brauchst, kannst du mit dem folgenden Quiz überprüfen:
Ergebnisse
