4,50 von 5 Sterne
Loading...
Bei dem Stichwort Satz des Pythagoras kommt einem direkt a2 + b2 = c2 in den Kopf. Doch was hat es damit eigentlich auf sich und wozu kann man diese Gleichung benutzen? Das werden wir dir jetzt Schritt für Schritt erklären.
Na, dann los!
Um mit dem Satz des Pythagoras rechnen zu können, muss ein rechtwinkliges Dreieck vorliegen.
Satz des Pythagoras Formel:
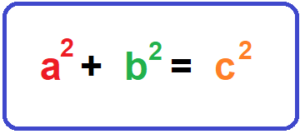
Zuerst müssen wir wichtige Begriffe im rechtwinkligen Dreieck definieren.
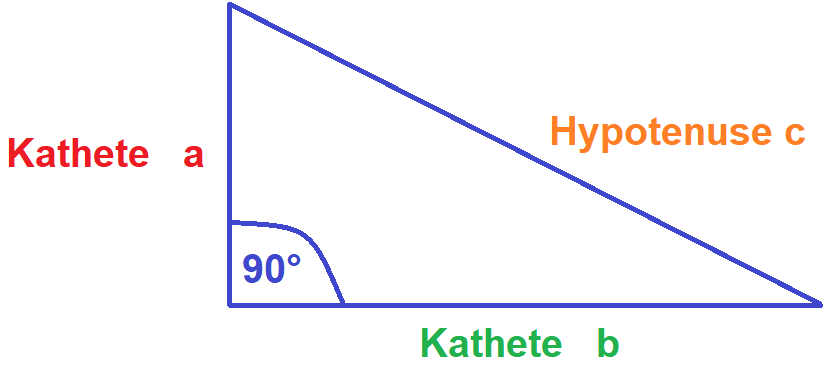
Die längste Seite im Dreieck (Hypotenuse) liegt immer gegenüber dem rechten Winkel (90°) und wird mit einem c gekennzeichnet.
Die beiden anderen Seiten, die direkt am rechten Winkel liegen nennt man Katheten. Sie sind die beiden kürzeren Seiten im Dreieck und werden mit a und b gekennzeichnet.
Wie berechnet man den Satz des Pythagoras?
In einem rechtwinkligen Dreieck ist die Summe der Kathetenquadrate gleich dem Quadrat der Hypotenuse.
Aber was genau ist mit diesem Satz gemeint?
Schauen wir uns dazu folgende Abbildung an:
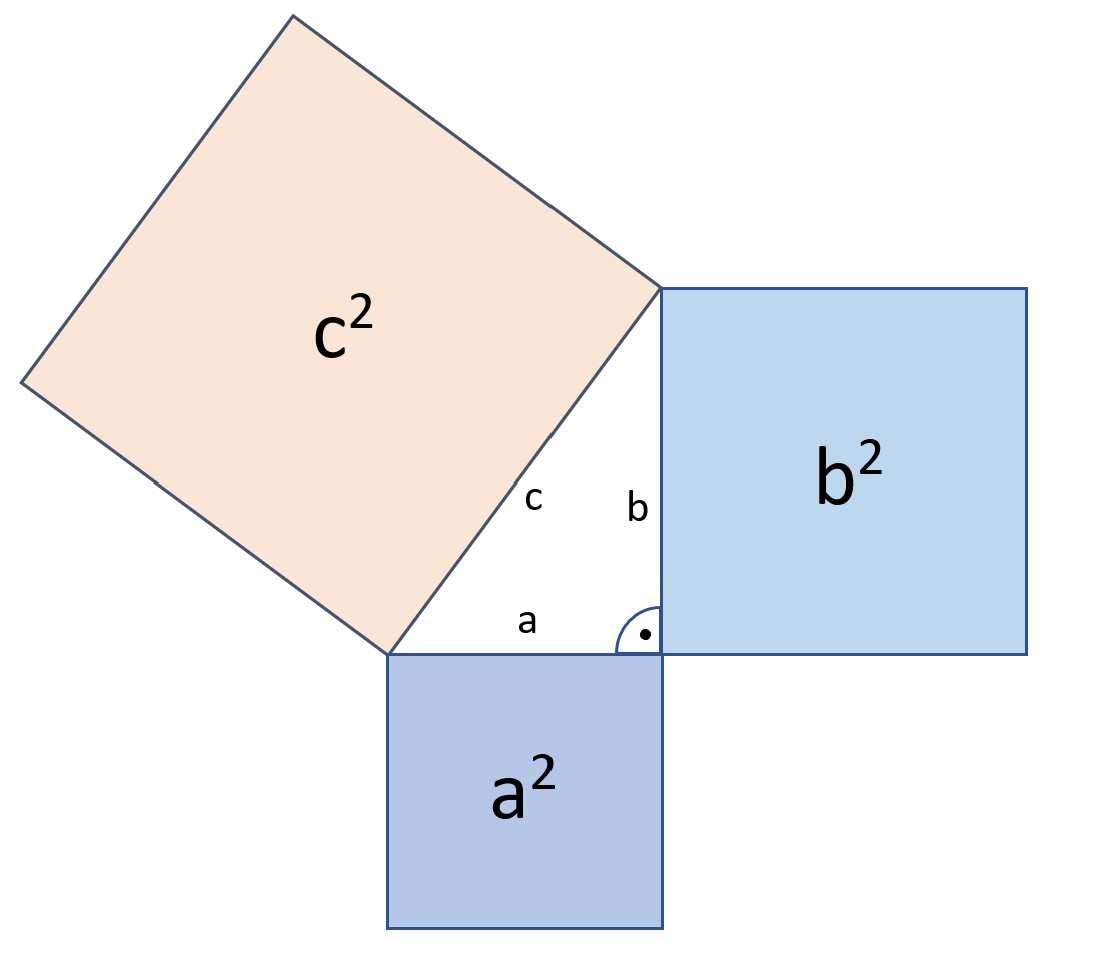
Um auf diese Abbildung zu kommen, haben wir über jede Seite des rechtwinkligen Dreiecks ein Quadrat gezeichnet.
So hat das Quadrat über der Seite a die Seitenlängen a und somit den Flächeninhalt a2. Führt man diesen Schritt bei allen Seiten des Dreiecks durch, so erhält man drei Quadrate mit den Flächeninhalten a2 , b2 und c2.
Der Satz des Pythagoras besagt, dass die Summe aus a2 und b2 gleich c2 ist.
Um dies zu veranschaulichen, kannst du dir gerne dieses kurze Video anschauen.
Mit dieser Formel in der Form können wir aber noch nicht die Seitenlänge bestimmen, sondern nur den Flächeninhalt der Quadrate über den Seiten.
Um auf eine Seitenlänge zu kommen, müssen wir noch die Wurzel ziehen. Somit lautet die Formel, mit der wir die Seitenlänge c bestimmen können:
BEACHTE!
Die Wurzel aus einer Quadratzahl ist die Zahl selbst, somit ergibt sich:
= c
a2 und b2 stehen aber gemeinsam unter der Wurzel. Also können wir aus der Summe a2 + b2 nicht einfach die Summe aus a + b machen (Wurzelgesetz).
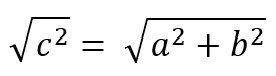
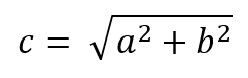
Du hast jetzt verstanden, was der Satz des Pythagoras besagt und wann du ihn anwenden kannst.
Satz des Pythagoras Beispiel
Angenommen das folgende rechtwinklige Dreieck beinhaltet folgende Werte
Gegeben: a= 5cm b= 12 cm Gesucht: c
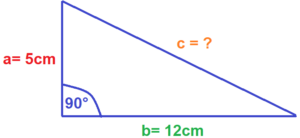
1. Zunächst setzt du die beiden Werte a und b in die Formel ein.
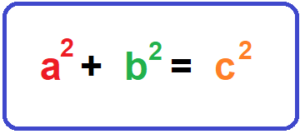
2. Als nächstes quadrierst du die beiden Katheten a und b. Anschließend addierst du die beiden Katheten zusammen.
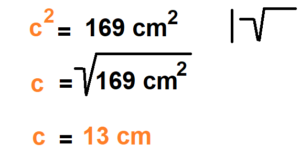
3. Zum Schluss ziehst du die Wurzel und erhältst das Ergebnis der Seitenlänge c.
Satz des Pythagoras umstellen
Der Satz des Pythagoras lässt sich beliebig nach allen Seiten, je nachdem welche Seite gesucht ist, umstellen.
Die Formel lautet: a2 + b2 = c2
Ist die Seite a oder b gesucht, kannst du die Formel umstellen.
Mit dieser Formel kannst du die Seitenlänge a des rechtwinkligen Dreiecks berechnen.
Genau nach derselben Methode kannst du die Formel für die Seitenlänge b umstellen.
Satz des Pythagoras – Aufgaben
Ergebnisse
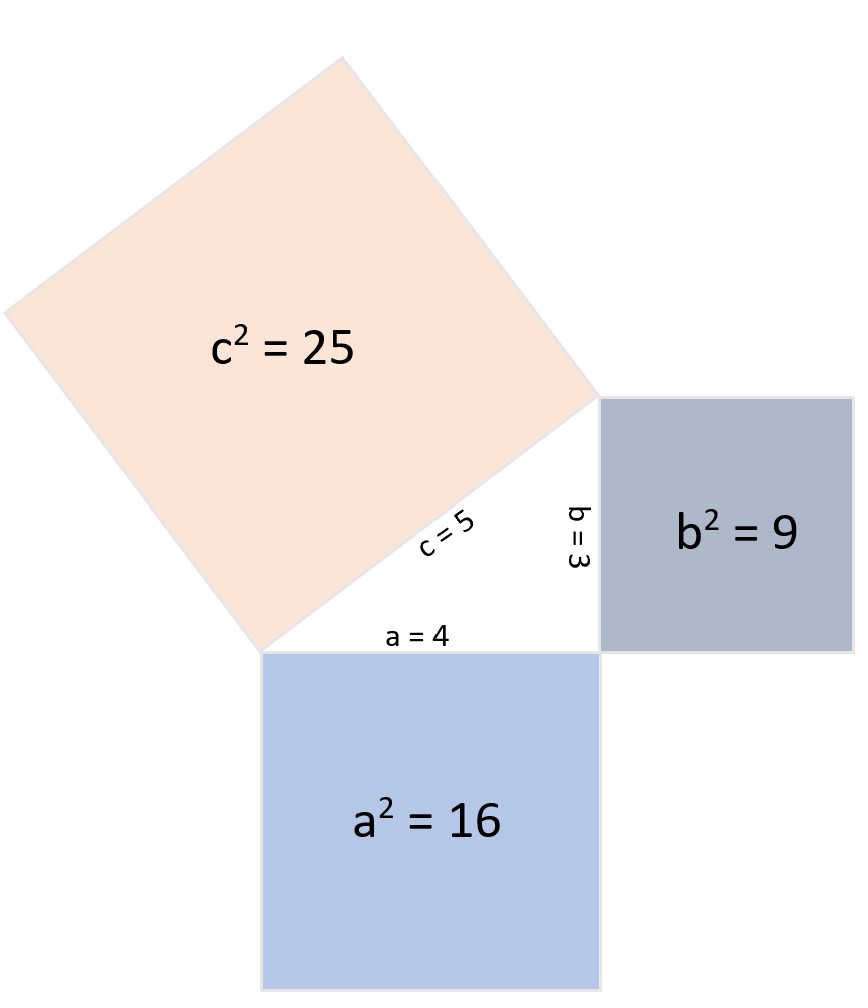
#1. Wie lang ist die Seite c eines Dreiecks mit den Katheten b=4 und a=3?
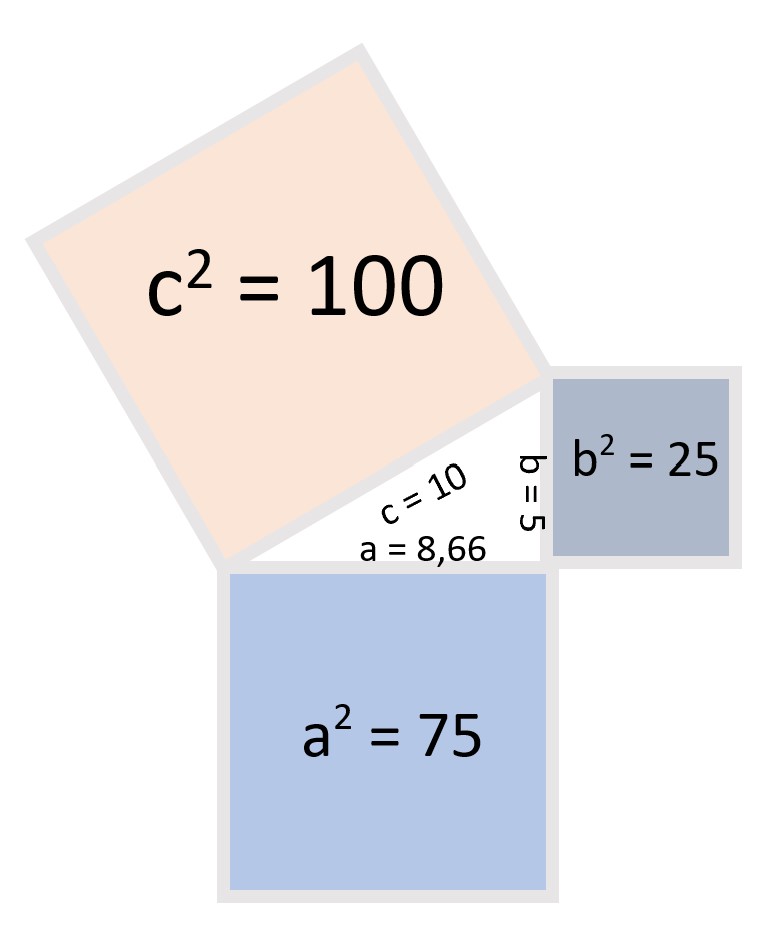
#2. Wie lang ist die Seite a eines Dreiecks mit den Seitenlängen c=10 (Hypotenuse) und b=5 (Kathete)?
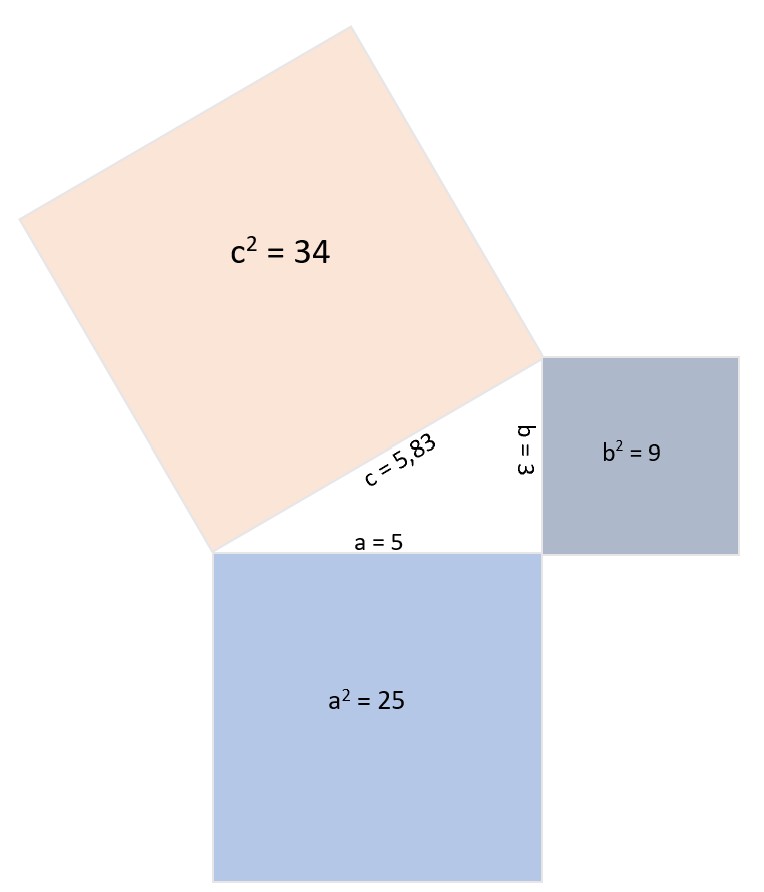
#3. Wie lang ist die Seite c eines Dreiecks mit den Katheten-Quadraten a^2 = 25 und b^2 = 9?
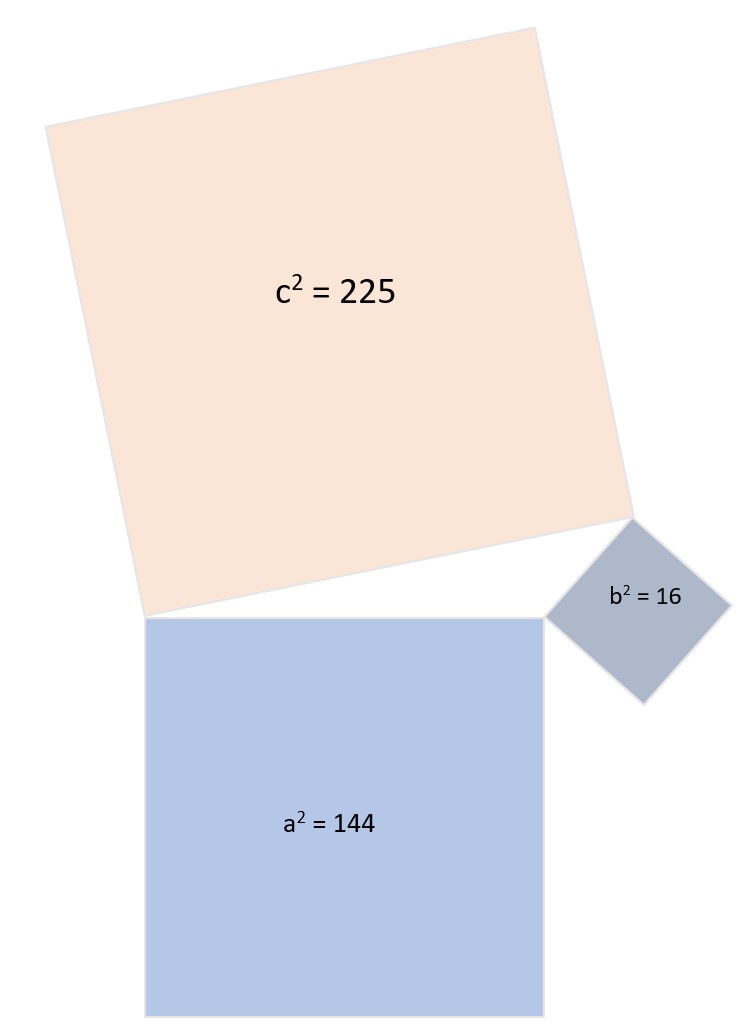
#4. Ist ein Dreieck mit den Seitenlängen a = 4 , b = 12 und c = 15 ein rechtwinkliges Dreieck?
c2= a2 + b2 | Werte einsetzen
c2 = 42 + 32 | Wurzel ziehen
c = 5
Als erstes müssen wir die Formel für den Satz des Pythagoras nach a^2 umstellen.
a2 + b2 = c2 |- b2
a2 = c2 – b2 |Werte einsetzen
a2 =102 – 52|Wurzel ziehen
a = 8,66
c2 = a2 + b2 | Werte einsetzen
c2 = 25 + 9 |Wurzel ziehen
c = 5,83
Bei jedem rechtwinkligen Dreieck stimmt der Satz des Pythagoras und die Gleichung a2 + b2 = c2. Daraus können wir schließen: Stimmt die Gleichung nicht, liegt kein rechtwinkliges Dreieck vor.
Wir müssen nun überprüfen, ob die Summe aus 122 + 42 einem Wert von 152 entspricht.
122 + 42 = 160
152 = 225
160 ≠ 225
Da somit die Gleichung nicht stimmt, handelt es sich bei dem Dreieck nicht um ein rechtwinkliges Dreieck.
FAQ zum Satz des Pythagoras
Was besagt der Satz des Pythagoras?
In einem rechtwinkligen Dreieck ist die Summe der Kathetenquadrate gleich dem Quadrat der Hypotenuse.
Wie lautet die Formel für den Satz des Pythagoras?
Die Formel für den Satz des Pythagoras lautet: a2 + b2 = c2
Wann kann du den Satz des Pythagoras anwenden?
Den Satz des Pythagoras kannst du immer anwenden, wenn du ein rechtwinkliges Dreieck vorliegen hast.
Diese Themen könnten ebenfalls interessant für dich sein:
Ich bin Schülerin und habe mit dieser Website den Satz des Pythagoras gelernt. Sehr gute und einfach Erklärung und ideale Aufgaben zum üben. Vielen dank!