4,86 von 5 Sterne
Loading...
In Mathe ist gerade das Thema Prismen dran und du suchst eine simple Erklärung dafür? Dann bist du hier richtig!
Du erfährst bei uns Schritt für Schritt:
- was ein Prisma ist
- was Beispiele dafür sind
- wie man es berechnet
- was Prismen Netze sind
Am Ende erwarten dich noch ein paar Übungen und ein FAQ, um deine Fragen zu klären.
Los geht’s!
Prismen Definition
Ein Prisma ist ein dreidimensionaler Körper. Er hat auf der einen Seite eine Grundfläche mit mind. drei Ecken. Außerdem hat er gleich lange und parallele Kanten, die von dieser Grundfläche aus verlaufen. Auf der gegenüberliegenden Seite befindet sich eine Deckfläche. Diese ist kongruent, also deckungsgleich, zur Grundfläche.
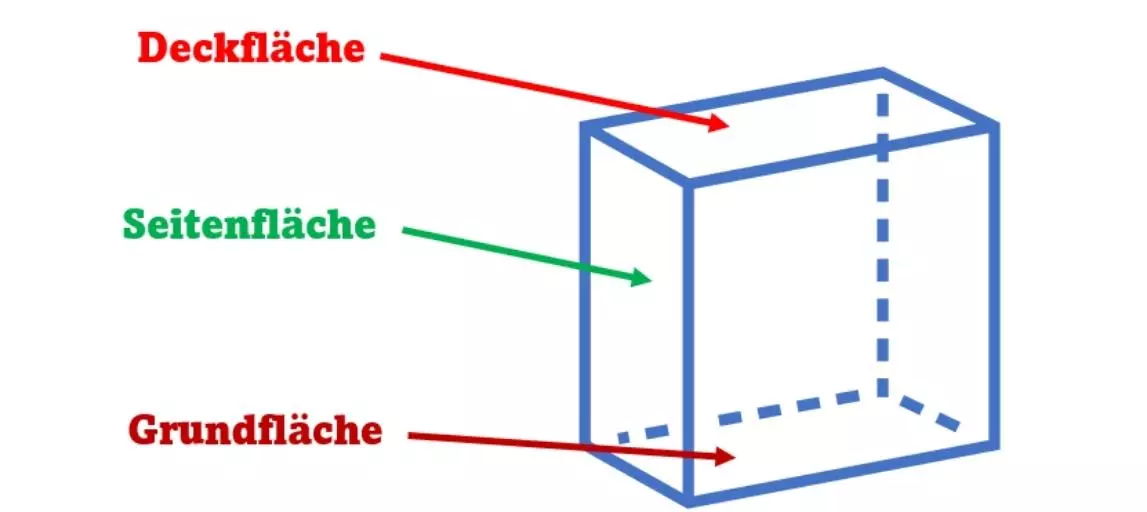
Prisma Eigenschaften
Die Grundfläche und die Deckfläche sind deckungsgleiche Vielecke, die parallel zueinander sind.
Die Seitenflächen stehen senkrecht auf der Grundfläche.
Bei einem geraden Prisma sind die Seitenflächen Rechtecke.
Gerade und schiefe Prismen
So ein Vieleck ist gerade, wenn sich seine parallelen Kanten senkrecht auf der Grundfläche befinden. Wenn das nicht der Fall ist, wird es als schief bezeichnet.
Meistens schaut ihr euch im Matheunterricht nur gerade Prismen an.
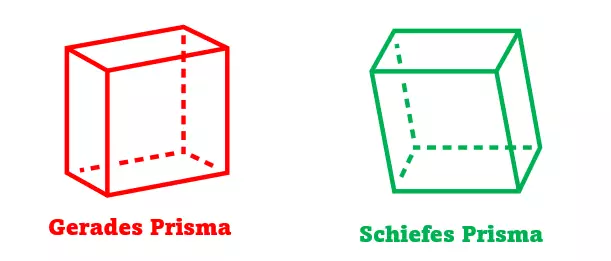
Prismen Arten
Es gibt verschiedene Prismen mit unterschiedlich vielen Ecken bzw. Seitenflächen. Hat es drei Seitenflächen, wird es dreiseitig genannt. Bei vier Seiten heißt es vierseitig und so weiter.
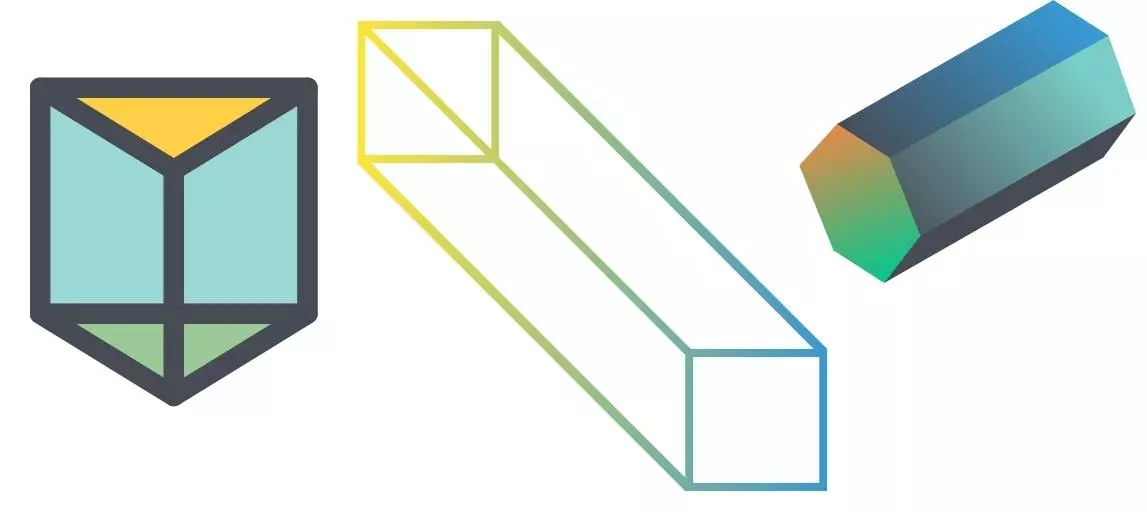
Prismen Beispiele
Beispiele für gerade Prismen sind der Würfel oder der Quader.
Ein Würfel besteht aus sechs Quadraten, während beim Quader die Grund- und Deckflächen aus Rechtecken oder Quadraten bestehen.
Schau dir hierzu gerne unseren Artikel über Quader an!
Eine Pyramide oder ein Kegel sind keine Prismen.
Bei beiden Körpern hat die Grundfläche jeweils nämlich keine deckungsgleiche und parallele Deckfläche!
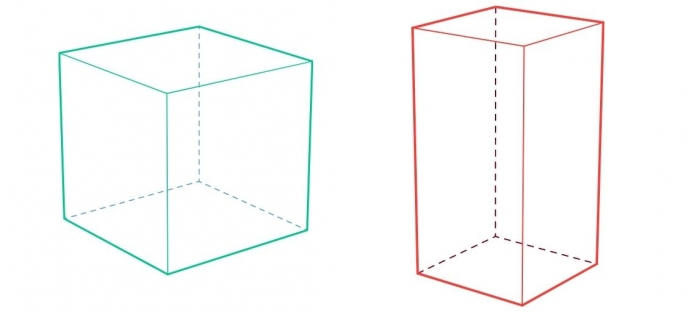
Prismen berechnen
Es gibt viele unterschiedliche Arten von solchen Vielecken. Wenn du etwas an ihnen berechnen möchtest, musst du das immer beachten.
Generell können bei ihnen Umfang, Mantelfläche, Oberfläche und Volumen berechnet werden.
Wir zeigen dir im nächsten Schritt anhand von einem Dreiecksprisma, wie einfach das geht!
Umfang berechnen
Den Umfang U kannst du leicht berechnen, indem du alle Seiten des Körpers miteinander addierst.
Hier findest du weitere Infos zur Umfang Berechnung!
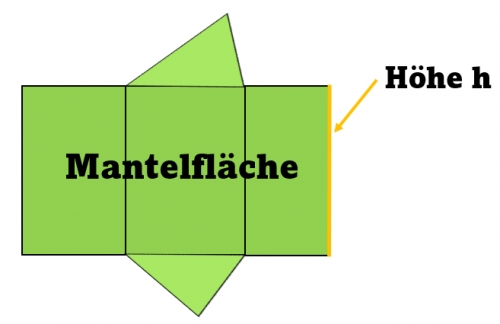
Mantelfläche Prisma
Die Mantelfläche M berechnest du, indem du du den Umfang mit der Höhe des Prismas multiplizierst.
Die Formel dazu lautet:
Oberflächeninhalt Prisma
Die Oberfläche dieses Vielecks setzt sich zusammen aus den zwei Grundflächen und der Mantelfläche.
Die Formel ist:
Prisma Volumen
Das Volumen ist der räumliche Inhalt eines Körpers. Mit folgender Formel lässt sich das Volumen berechnen:
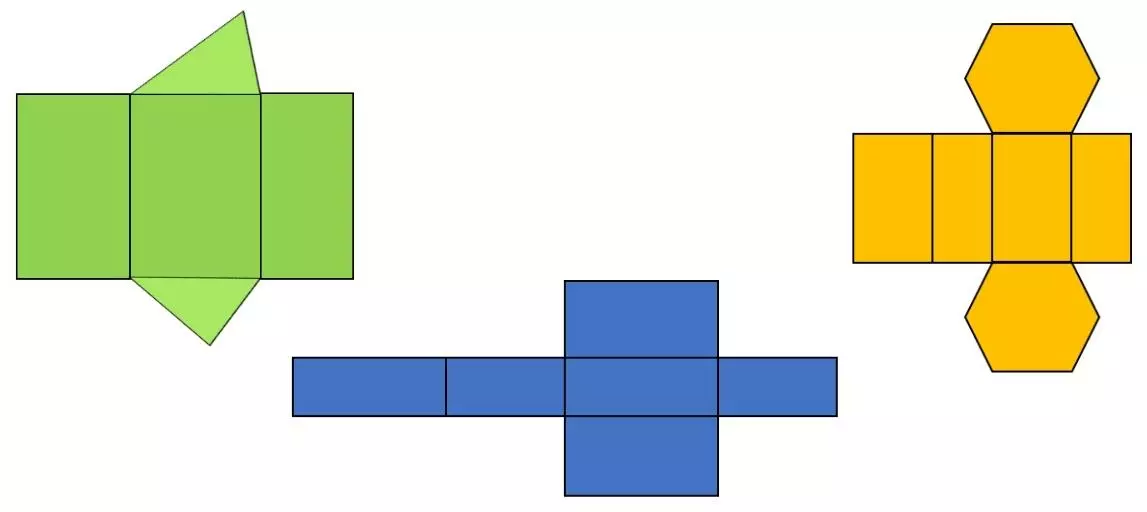
Prismen Netze
Wenn du es auseinander klappst, erhältst du ein sogenanntes Prisma Netz. Um noch leichter zu verstehen, was so etwas ist, zeigen wir dir hier die Netze von einem dreiseitigen, vierseitigen und sechsseitigen Prisma:
Prismen im Alltag
Wenn du darauf achtest, begegnen dir viele solcher Vielecke im echten Leben! Ein Prisma im Alltag ist zum Beispiel eine sechseckige Geschenkschachtel oder ein Würfel.
Prismen Formeln
Wir haben dir die Prisma Formeln zum Herunterladen erstellt. In der Formelsammlung ist nochmal alles Wichtige zusammengefasst.
Beachte, dass bei den verschiedenen Grundflächen der Prismen auch die Formeln unterschiedlich sein können. Zum Beispiel ist die Berechnung der Mantelfläche eines Dreiecksprismas etwas anders als die der Mantelfläche eines Quaders!
Formel Tabelle
Hier siehst du eine Tabelle, die die Berechnungen für die verschiedenen Prismen Arten zeigt:
Übungen
Probiere es mit der Formelsammlung und der Tabelle selbst aus und bearbeite die folgenden Übungen!
Ergebnisse
#1. Erkläre, was ein Prisma ist.
#2. Erkläre, welche Arten es von Prismen gibt.
#3. Wie ist die Oberfläche für ein rechteckiges Prisma mit den Maßen a = 10 cm, b = 5 cm und c = 10 cm?
#4. Wie ist die Mantelfläche für ein dreieckiges Prisma mit den Maßen a = 4 cm, b = 4 cm, c = 4 cm und h = 3,5 cm?
#5. Wie ist das Volumen für einen Quader mit den Maßen a = b = c = 5 cm?
Wir hoffen, dass wir dir weiterhelfen konnten!
Um letzte Fragen zu klären, folgt ein FAQ.
Klicke einfach auf das +, um dir die Antworten anzusehen.
FAQ – Häufig gestellte Fragen
Was sind Prismen?
Es sind dreidimensionale Körper. Dieser hat immer eine Grundfläche und eine Deckfläche. Beide sind deckungsgleiche und parallele Vielecke.
Was sind die Eigenschaften von Prismen?
Die Grundfläche und die Deckfläche sind deckungsgleiche Vielecke, die parallel zueinander sind.
Die Seitenflächen stehen senkrecht auf der Grundfläche.
Es gibt gerade und schiefe Prismen.
Was sind Beispiele für Prismen?
Beispiele sind Würfel, Quader oder Achteck. Im Alltag kann es z.B. eine sechsseitige Geschenkschachtel sein.
Wie werden Prismen berechnet?
Es gibt verschiedene Berechnungen für Prismen.
Generell kann man dafür Umfang, Mantelfläche, Oberfläche und Volumen berechnen.
In unserer Formelsammlung und der Tabelle sind alle gängigen Formeln zur Berechnung von Prismen zusammengefasst.
Was sind Prismen Netze?
Ein auseinander geklapptes Prisma wird Netz genannt. Es hat eine Grund- und Deckfläche sowie eine Mantelfläche.