3,93 von 5 Sterne
Loading...
Fragst du dich “Was sind natürliche Zahlen”, oder “Was ist der Unterschied zwischen natürlichen und ganzen Zahlen”? Wir haben die Antworten für Dich!
In diesem Artikel lernst du alles, was du über natürliche Zahlen wissen musst. Am Ende gibt es noch ein Quiz, in dem du dein Wissen über natürliche Zahlen testen kannst.
Lasst uns loslegen!
Was sind natürliche Zahlen?
Die Natürliche Zahlen ℕ sind eine Menge, zu der alle Zahlen gehören, die wir zum Zählen benutzen. Das heißt: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11 usw.
Wichtig ist, dass dies nur die ganzen Zahlen, anders gesagt, nur die vollständigen, positiven Zahlen sind. Kommazahlen, negative Zahlen oder Brüche gehören nicht dazu.
Ob die 0 dazu gehört hängt von der Definition ab. Gelten alle positiven ganzen Zahlen als natürlich Zahlen, gehört die 0 nicht dazu. Gelten alle nicht-negativen ganzen Zahlen, gehört die 0 dazu. Dies ist mathematisch aber nicht eindeutig festgelegt.
Natürliche Zahlen Zeichen
Das Zeichen ist ℕ. Dieses Zeichen ist kein normales N, sondern ein N mit einem zweiten Querstrich in der Mitte des N. Das Symbol wurde 1889 von Giuseppe Peano, einem bedeutenden italienischen Mathematiker und Logiker eingeführt.
Neben den natürlichen Zahlen gibt es u.a. auch die ganzen Zahlen ℤ und die rationalen Zahlen ℚ.
Natürliche Zahlen Definition
Natürliche Zahlen, sind alle positiven ganzen Zahlen.
ℕ = {1, 2, 3, 4,…}
Unterschied natürliche Zahlen ganze Zahlen
Der Unterschied zu den ganzen Zahlen (ℤ) ist recht einfach. Sie erweitern die nat. Zahlen mit den negativen Zahlen.
Das bedeutet, dass z.B. 5 sowohl in den nat. als auch den ganzen Zahlen enthalten ist, -5 aber nur in den ganzen Zahlen.
ℕ = {1, 2, 3, 4,…}
ℤ = {…-4, -3, -2, -1, 0, 1, 2, 3, 4,…}
Unterschied natürliche Zahlen rationale Zahlen
Rationale Zahlen (ℚ) erweitern ganzen Zahlen um Bruchzahlen, die sowohl im Zähler als auch im Nenner eine ganze Zahl haben. Diese Brüche kannst du natürlich auch als Kommazahl darstellen ( \frac{1}{2} ist auch 0,5).
Somit beinhalten rationale Zahlen z.B. die 4, die -4 aber auch \frac{16}{7} bzw. 2,286 oder – \frac{16}{7} bzw. -2,286.
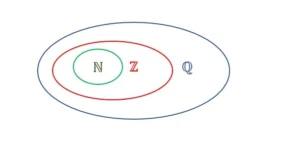
Zahlenmengen Darstellung
Wir haben für dich visuell dargestellt, welche Zahlenmenge (Nat., Ganze und Rationale Zahlen) welche andere beinhaltet:
Brüche mit natürlichen Zahlen multiplizieren
Um einen Bruch mit einer Zahl zu multiplizieren musst du so vorgehen:
1. Die natürliche Zahl in einen Bruch umwandeln. Dabei ist die nat. Zahl der Zähler, während die 1 der Nenner ist.
2. Die beiden Brüche miteinander multiplizieren
3. Gegebenenfalls das Ergebnis kürzen
Beispiel 4 x \frac{3}{2}:
1. 4 = \frac{4}{1}
2. \frac{4}{1} x \frac{3}{2} = \frac{12}{2}
3. \frac{12}{2} = \frac{6}{1} = 6
Für mehr Informationen und die Berechnung von Brüchen mit ganzen Zahlen kannst du hier klicken: Bruch multiplizieren mit ganzer Zahl
Übersichtstabelle Zahlenarten
Eine Übersichtstabelle als Zusammenfassung der vorgestellten Zahlenarten.
Definition: Natürliche Zahlen sind alle positiven ganzen Zahlen.
Beispiel: 1, 2, 3, 4, …
Symbol: ℕ
Definition: Alle natürlichen Zahlen und die negativen ganzen Zahlen.
Beispiel: …-3, -2, -1, 0, 1, 2, 3…
Symbol: ℤ
Definition: Alle ganzen Zahlen und alle Bruch- und Kommazahlen.
Beispiel: …-3,5…-0,7… 2,15,… 15…
Symbol: ℚ
Quiz – Teste dein Wissen!
Beantworte alle Fragen, indem du die richtige Antwort anklickst! Am Ende einfach auf den “Finish”-Button drücken, danach siehst du ob du richtig oder falsch lagst!
Alles richtig, du hast es drauf!
#1. Welche der folgenden Zahlen ist eine Natürliche Zahl?
#2. Welche der folgenden Zahlen ist eine Natürliche Zahl?
#3. Welche dieser Zahlen ist keine natürliche Zahl?
#4. Handelt es sich bei der Zahl 240 um eine natürliche, ganze oder rationale Zahl?
#5. Handelt es sich bei der Zahl -3,2 um eine natürliche, ganze oder rationale Zahl?
Ergebnisse
Häufig gestellte Fragen / FAQ
Die Natürliche Zahlen ℕ sind eine Menge, zu der alle Zahlen gehören, die wir zum Zählen benutzen. Das heißt: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11 usw.
Wichtig ist, dass dies nur die nur die “vollständigen” positiven Zahlen sind. Kommazahlen, negative Zahlen oder Brüche gehören nicht dazu.
Das Zeichen für nat. Zahlen ist ℕ
Die ganzen Zahlen erweitern die nat. Zahlen mit den negativen Zahlen. Die nat. Zahlen enthalten 1, 2, 3, 4 usw., während die ganzen Zahlen dazu noch -1, -2, -3, -4 usw. enthalten.