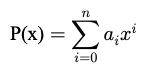4,80 von 5 Sterne
Loading...
Wie rechnet man richtig mit Koeffizienten? Wie vergleicht man Koeffizienten miteinander? Oder wofür braucht man Koeffizienten überhaupt? All das erklären wir dir hier:
Ausgeschrieben lautet er dann:
Am Anfang des Polynoms fehlt das x^0. Wie du dich vielleicht erinnerst, ergibt alles, was hoch 0 genommen wird, 1. Bist du dir bei Rechnungen mit Potenzen unsicher, kannst hier mehr über die Potenzgesetze nachlesen.
Koeffizientenvergleich
Ein Koeffizientenvergleich ist ein Verfahren, mit dem festgestellt werden kann, ob zwei Polynome gleich sind.
Gegeben sind die zwei Polynome:
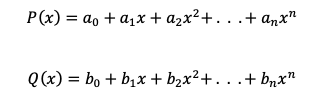
Beide diese Polynome haben die die gleiche höchste Potenz n, das bedeutet, sie haben den gleichen Grad.
Wenn nun auch noch alle Koeffizienten gleich sind (also a_n=b_n), dann sind auch die beiden Polynome gleich.
Aber man kann mit einem Koeffizientenvergleich nicht nur herausfinden, ob zwei Polynome gleich sind, sondern sie auch gleich machen.
Sehen wir uns hierfür ein Beispiel an:
Wir nehmen die zwei Polynome P(x) und Q(x)
P(x)=4x-1
Q(x)=a(x-1)+2b
Zuerst multiplizieren wir Q(x) aus:
Q(x)=a(x-1)+2b=ax-a+2b
Als nächstens müssen wir den Grad und die Koeffizienten bestimmen:
Der Grad die höchste Potenz von x, in diesem Fall also 1.
Die Koeffizienten einmal sind die Zahlen vor der Unbekannten x. Hier sind das 4 und a:
P(x)=4x-1
Q(x)=ax-a+2b
Das sind aber noch nicht alle Koeffizienten. Es gibt ja noch Zahlen in der Funktion, die nicht die Unbekannte x sind. Das sind konstante Werte. Sind die denn auch Koeffizienten?
Ja. Diese sind nämlich die Koeffizienten von x^o. Wie wir oben schon in der Infobox gezeigt haben, gilt x^o=1, deswegen steht es nicht da. Also können wir auch die Reste der Funktionen hernehmen:
P(x)=4x-1
Q(x)=ax-a+2b
Der Schönheit halber setzten wir nun P(x) und Q(x) gleich:
P(x)=Q(x)
4x-1=ax-a+2b
Durch das Gleichsetzten der Koeffizienten kommen wir auf folgende Gleichungen:
4x=ax
-1=2b-a
Jetzt müssen wir auflösen. In der ersten Gleichung können wir das x ganz einfach rauskürzen:
4x = ax
a = 4
Jetzt ist dir bestimmt schon aufgefallen, dass wir a=4 in die zweite Gleichung einsetzten können. So kommen wir auch auf b:
-1 = 2b-4
3 = 2b
b = 1,5
Wenn also a = 4 und b = 1,5, dann sind P(x) und Q(x) gleich.
Zum Thema siehe auch: Kreuzprodukt, Extremwertaufgabe, pq-Formel
Das Koeffizienten-Quiz
Ergebnisse
#1. Was ist ein Koeffizient?
#2. Was ergibt x^0?
#3. Was ist die Vorraussetzung für einen Koeffizientenvergleich?
Häufige Fragen und Antworten
Was ist ein Koeffizient?
Ein Koeffizient ist die Vorzahl einer Unbekannten.
Was kann man mit Koeffizienten manchen?
Haben zwei Polynome die den gleichen Grad, kann man die Koeffizienten gleichsetzten, um die Polynome gleich zu machen.
Wo kommen Koeffizienten noch vor?
Gerade in der Physik wird auch viel mit Koeffizienten gerechnet. So gibt es den Reibungskoeffizienten und den Stromwiderstandskoeffizieten. Auch in der Chemie gibt es zum Beispiel den Bindungskoeffizienten.
Wir haben viel Mühe in diesen Artikel gesteckt und freuen uns riesig, wenn du uns eine Sternebewertung oder einen Kommentar hinterlässt. Vielen Dank! ?
4,80 von 5 Sterne
Loading...
Das könnte ebenfalls interessant für dich sein:
