5,00 von 5 Sterne
Loading...
Die Kettenregel wird häufig bei Ableitungen von Funktionen angewendet. Doch wie funktioniert sie genau und worauf muss man achten? Wir zeigen es dir.
Lass uns beginnen!
Die Kettenregel brauchst du, wenn du eine verkettete Funktion ableiten möchtest. Wir zeigen dir, wie so eine verkettete Funktion aussieht und rechnen sie dir an drei Beispielen vor.
Zum Thema siehe auch: Kreuzprodukt, Extremwertaufgabe, pq-Formel
Kettenregel Rechnungen
1. Beispiel
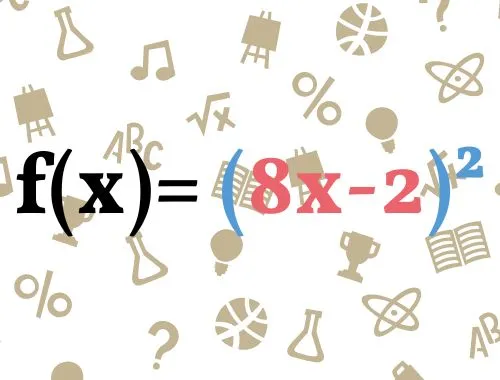
In der Abbildung haben wir dir eine Beispielfunktion angegeben. Woran erkennen wir an dieser Funktion eine Verkettung? Um dir das zu verdeutlichen, haben wir die innere und äußere Funktion farbig markiert. Sobald eine Funktion so aussieht, kommt die Kettenregel ins Spiel.
Wir haben also eine innere Funktion, die in der Klammer steckt und wir haben eine äußere Funktion, das ist das, was das Ganze umschließt. In dem Fall die Klammer mit dem Exponenten.
Die Ableitung von einem Ganzen können wir bilden, indem wir die innere Ableitung bilden und mit der äußeren Ableitung multiplizieren.
Kettenregel: innere Ableitung * äußere Ableitung
Wenn wir also die erste Ableitung aus der inneren Funktion bilden ist es nichts anderes als f'(x)= 8. Leiten wir nun die äußere Funktion ab, ist es auch nicht anderes als f'(x) = 2(8x-2). Das heißt, der Exponent mit 2 geht nach vorne und wird immer mit -1 abgezogen. Die erste Ableitung könnte auch so aussehen: f'(x)=2(8x-2)1
Meistens schreibt man die hoch 1 aber nicht hin, sie wird einfach weg gelassen.
Nun müssen wir nur noch unsere innere Ableitung mit der äußeren Ableitung multiplizieren. Das wäre in dem Fall f'(x)= 8*2(8x-2). Die erste Ableitung der Funktion mithilfe der Kettenregel ist somit gelöst.
Wichtig zu erwähnen ist, dass bei der abgeleiteten äußeren Funktion die Funktion in der Klammer unverändert bleibt. Das, was in der Klammer steht, schreiben wir normal ab – ohne es abzuleiten.
2. Beispiel
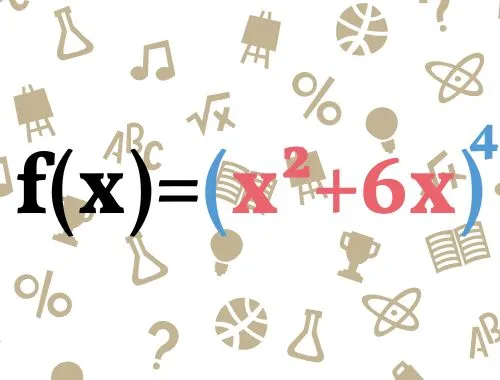
Auch bei dieser Funktion wenden wir die Kettenregel an. Zuerst die innere Funktion ableiten, das wäre f'(x)=2x+6. Danach die äußere Ableitung ableiten, das wäre f'(x)=4(x²+6x)3.
Der Exponent 4 kommt nach vorne und wir ziehen von der 4 wieder einen ab, so dass es 3 ergibt. Wenn wir die innere und äußere Ableitung miteinander multiplizieren, erhalten wir f'(x)=(2x+6)*4(x²+6x)3
Die Ableitung ist somit fertig.
3. Beispiel
Wie wenden wir aber die Kettenregel bei einer E-Funktion an?
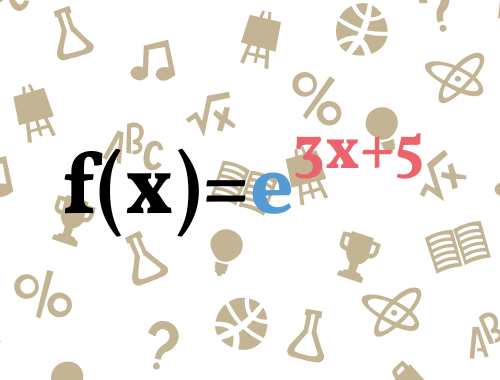
Die innere Funktion ist in dem Fall das, was im Exponent steht – also 3x+5. Dieses müssen wir nur ableiten. Abgeleitet wäre das f'(x)=3. Die äußere Funktion bei der E-Funktion ist immer e. Wenn wir sie ableiten wollen, übernehmen wir einfach das e mit dem Exponenten. Also in dem Fall f'(x)=e3x+5.
Multiplizieren wir die innere mit der äußeren Funktion, so ergibt sich f'(x)=3*e3x+5.
Quiz zur Kettenregel
Zum krönenden Abschluss haben wir noch 3 Aufgaben vorbereitet, die du eigenständig lösen kannst.
Wählen Sie alle zutreffenden:
Ergebnisse
#1. Bilde die erste Ableitung von f(x)=(7×3-8×2)3
#2. Bilde die erste Ableitung von f(x)=(x3+10x)6
#3. Bilde die erste Ableitung von f(x)= e8x+3
Kennst du schon unsere Artikel zu Assoziativgesetz und Quotienten berechnen? Nein? Dann schau gerne mal rein!
Wir hoffen sehr, dass du die Kettenregel anhand der drei Beispiele gut verstanden hast. Falls noch Unklarheiten bestehen, nutze einfach die Kommentarfunktion und schreib uns, wo du noch Hilfe benötigst.
FAQ
Was lautet die Formel bei der Kettenregel?
Du multiplizierst die innere Ableitung mit der äußeren Ableitung zusammen.
Wann wende ich die Kettenregel an?
Sobald du eine Funktion wie in dem Fall f(x)=(x2+x)2 oder eine E-Funktion mit dem Exponenten x2+x hast, wendest du die Kettenregel an.
Hat dir der Beitrag zum Thema Kettenregel gefallen und geholfen? Dann würden wir uns riesig über eine Sternebewertung freuen. Bis zum nächsten Mal.
5,00 von 5 SterneLoading...
Das könnte ebenfalls interessant für dich sein: