3,86 von 5 Sterne
Loading...
Du möchtest wissen, was irrationale Zahlen sind? Hier wird dir in 3 Minuten mit Beispielen leicht erklärt…
… was irrationale Zahlen sind.
… wie sie bei den Zahlenarten einzuordnen sind.
… was der Unterschied zu rationalen und reellen Zahlen ist.
Am Schluss erwartet dich ein Quiz, damit du dein Wissen testen kannst.
Lass uns loslegen!
Was sind irrationale Zahlen?
Irrationale Zahlen sind das Gegenteil von rationalen Zahlen, denn sie beinhalten alle Zahlen, die nicht zu den rationalen Zahlen gehören.
Es sind also
- Dezimalzahlen mit unendlich vielen Nachkommastellen
- Wurzeln, die keine Quadratzahlen sind
- die Kreiszahl π
Solche Zahlen sind nicht periodisch, sie wiederholen sich also niemals.
Irrationale Zahlen Definition
Diese Zahlen sind nicht als Quotient zweier ganzer Zahlen darstellbar.
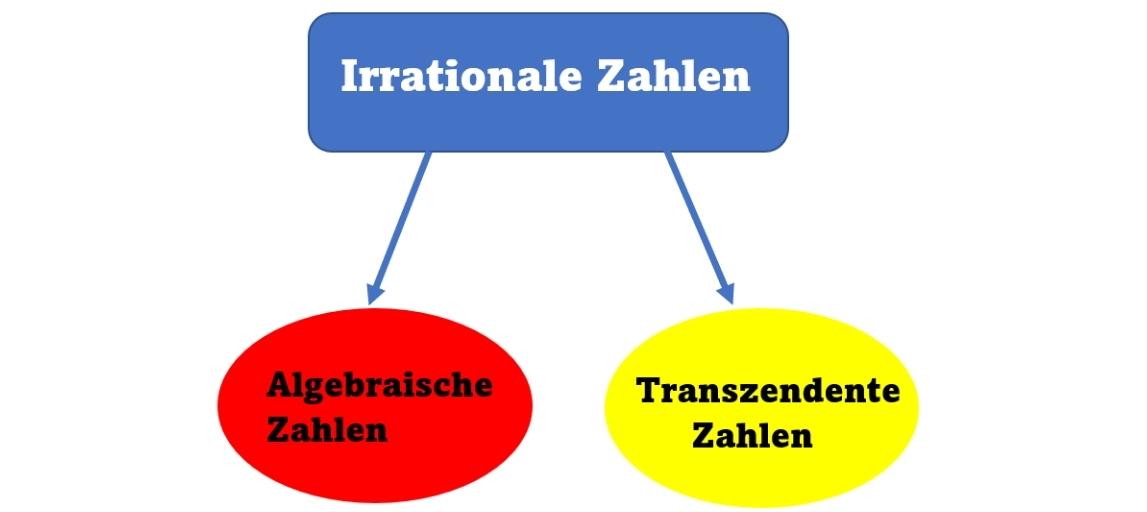
Generell werden sie in zwei Kategorien unterschieden:
- Algebraische Zahlen, wie zum Beispiel √2
- Transzendente Zahlen, wie zum Beispiel π
Irrationale Zahlen Symbol
Zusammen mit den rationalen Zahlen, die das Zeichen ℚ haben, sind diese Zahlen Teil der reellen Zahlen ℝ.
Deswegen wird folgendes Zeichen als Symbol für irrationale Zahlen verwendet:
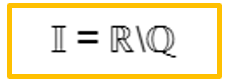
Irrationale Zahlen Beispiele
In diesem Zusammenhang bedeutet Irrationalität, dass diese Zahlen zwar nicht periodisch, dafür aber unendlich sind. Als Dezimalzahlen haben sie unendlich viele Nachkommastellen.
Beispiele für solche Zahlen sind -√5 oder auch die Zahl π.
Wusstest du, dass die eulersche Zahl e = 2, 718 281 828 459 045 235 360 287 471 352… somit auch irrational ist?
Sie hat unendlich viele Nachkommastellen und ist dabei nicht periodisch!
Zahlenarten
Wie du gerade gelesen hast, gibt es verschiedene Zahlenarten. Sicherlich hast du auch schon selbst von einigen gehört. Wir haben dir eine Auflistung erstellt und im Folgenden erklären wir dir kurz alle diese Arten von Zahlen, die mit den irrationalen Zahlen zu tun haben.
Rationale und irrationale Zahlen
Irrationale Zahlen hängen mit den rationalen Zahlen zusammen. Rationale Zahlen sind entweder Brüche aus ganzen Zahlen oder Dezimalzahlen. Bei solchen Brüchen ist sowohl der Zähler als auch der Nenner eine ganze Zahl.
Info: Schau dir gerne einmal unseren Artikel über rationale Zahlen an!
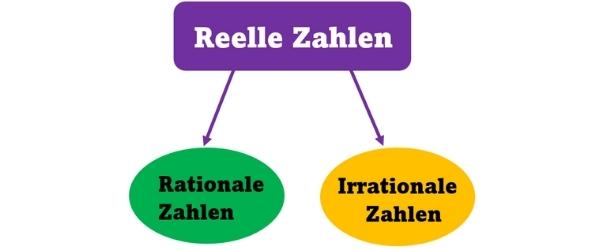
Reelle Zahlen
Zusammen ergeben die irrationalen und die rationalen Zahlen die reellen Zahlen ℝ.
Sie sind bedeutsam und vielfältig, da man Flächeninhalte, Längen oder auch Rauminhalte von verschiedensten geometrischen Körpern und Objekten mit ihnen beschreiben kann, die als rationale Zahlen oft nicht so dargestellt werden können.
Jetzt bist du an der Reihe!
Hier haben wir ein paar Übungen für dich erstellt, damit du dein neu erworbenes Wissen auf die Probe stellen kannst.
Übungen
Klicke einfach auf das +, um dir die richtige Antwort anzusehen!
Beschreibe, was irrationale Zahlen sind.
Sie sind das Gegenteil von rationalen Zahlen, denn sie beinhalten alle Zahlen, die nicht zu den rationalen Zahlen gehören.
Solche Zahlen sind nicht periodisch, also wiederholen sich niemals.
Es sind Dezimalzahlen mit unendlich vielen Nachkommastellen, Wurzeln (die keine Quadratzahlen sind) und die Kreiszahl π.
Ordne die irrationalen Zahlen in die verschiedenen Arten der Zahlen ein.
Diese Zahlen hängen mit den rationalen Zahlen zusammen. Rationale Zahlen sind entweder Brüche aus ganzen Zahlen oder Dezimalzahlen.
Zusammen ergeben die beiden Zahlenarten die reellen Zahlen ℝ.
Was ist der Unterschied zwischen irrationalen und rationalen Zahlen?
Rationale Zahlen sind entweder Brüche aus ganzen Zahlen oder Dezimalzahlen.
Irrationale Zahlen sind zwar auch Dezimalzahlen, allerdings sind sie nicht periodisch und haben unendlich viele Nachkommastellen. Es können auch Wurzeln (keine Quadratzahlen) oder die Kreiszahl π sein.
Ist √4 eine irrationale Zahl?
Nein, es ist eine rationale Zahl.
Ist 2,25 eine irrationale Zahl?
Nein, es ist eine rationale Zahl.
Ist -2xπ eine irrationale Zahl?
Ja, das ist richtig.
Übersichtstabelle Zahlenarten
Zahlenart | Symbol | Beispiel |
Natürliche Zahlen | ℕ | { 0, 1, 2…} |
Ganze Zahlen | ℤ | { …-1, 0, 1…} |
Rationale Zahlen | ℚ | {...-2/5, -1, 0, 1, 1/3…} |
Reelle Zahlen | ℝ | { …-1/3, 1, 0, 1, 2,3...} |
Hier kannst du die Tabelle über die Zahlenarten auch für dich herunterladen!
Darstellung der Zahlenmengen
Damit du es noch besser verstehst, haben wir dir hier die Zahlenarten und -mengen bildlich dargestellt:
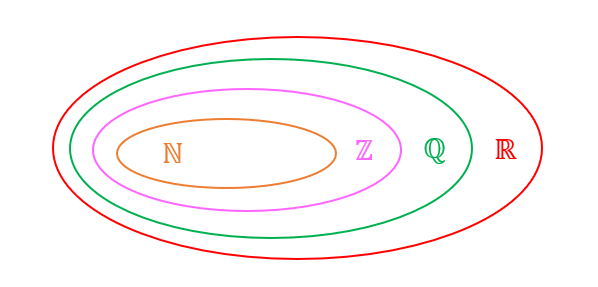
ℕ steht für die natürlichen Zahlen. Diese sind in den ganzen Zahlen ℤ beinhaltet, welche wiederum Teil der rationalen Zahlen ℚ sind.
Die rationalen Zahlen werden durch die reellen Zahlen ℝ erweitert. Diese Zahlen bestehen aus den rationalen und den irrationalen Zahlen.
Wir hoffen, dass wir dir die verschiedenen Zahlenarten verständlich machen konnten!
Nun hast du noch die Möglichkeit, dein Wissen durch ein Quiz zu testen.
Viel Spaß!
Quiz
Ergebnisse
#1. Was ist die Definition für irrationale Zahlen?
#2. Wie ist das Symbol für irrationale Zahlen?
#3. Was ist der Unterschied zwischen rationalen und irrationalen Zahlen?
#4. Ist -5 eine irrationale Zahl?
#5. Was ist eine irrationale Zahl
Wir geben uns mit unseren Ratgeber-Artikeln immer sehr viel Mühe.
Wie fandest du diesen Artikel?
Lass uns gerne eine Bewertung oder einen Kommentar da – wir würden uns sehr darüber freuen ?
3,86 von 5 SterneLoading...