4,27 von 5 Sterne
Loading...
Du hast im Unterricht gerade erst von den Ableitungsregeln gehört und plötzlich redet dein Lehrer vom Aufleiten und der Integralrechnung?
Und was ist eigentlich der Unterschied zwischen einem unbestimmten und einem bestimmten Integral?
Wir haben die wichtigsten Informationen und Rechenregeln zum Bilden von Integralen zusammengefasst und bringen dir mit Übungen und Beispielen näher, wie du den Flächeninhalt zwischen einer Funktion und der x-Achse berechnest.
Die Integralrechnung ermittelt krummlinig begrenzte Flächeninhalte und ist ein Gebiet der Analysis. Voraussetzung für die Berechnung von Flächenstücken ist dabei eine Funktion, welche im Intervall stetig, also nicht unterbrochen, ist.
Bei der Integration wird prinzipiell zwischen einem unbestimmten und einem bestimmten Integral unterschieden.
Für was braucht man Integrale?
Die Integralrechnung beschäftigt sich mit Flächen, die durch Funktionen krummlinig begrenzt sind, womit der Flächeninhalt A in einem gegebenen Intervall ermittelt werden kann.
Das Flächenstück A erkennst du in der nachfolgenden Abbildung.
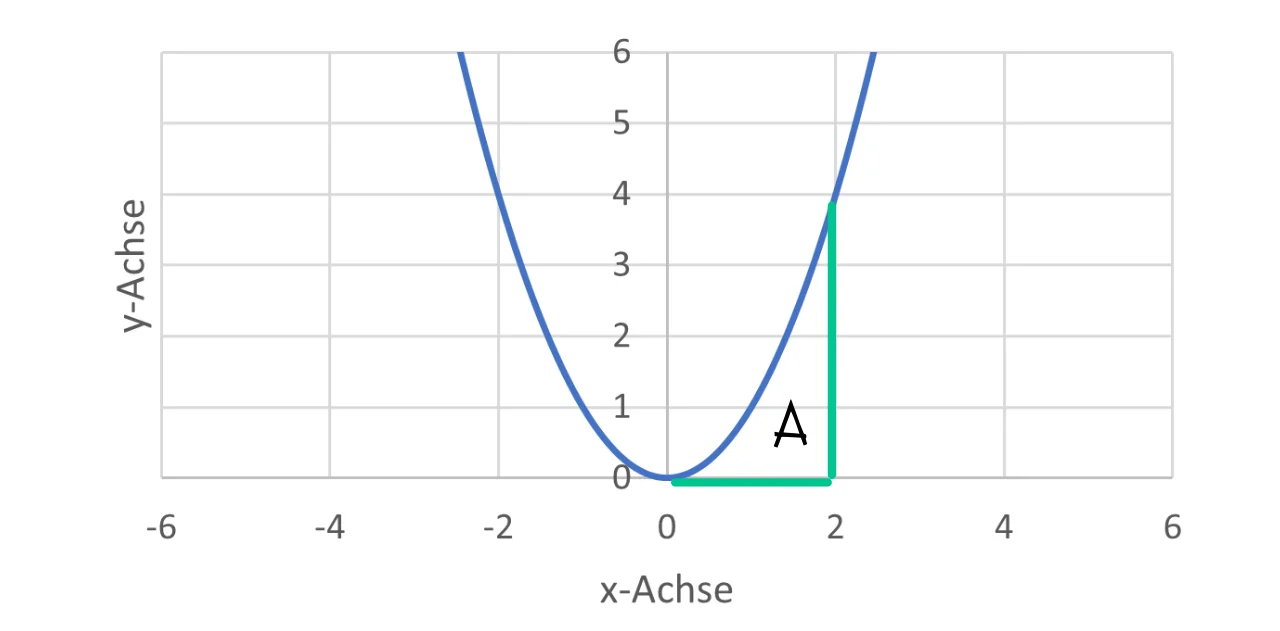
In dem Koordinatensystem ist die Funktion f(x)=x² gegeben. Die Fläche verläuft zwischen der Funktion und der x-Achse bis x=2 ist.
Um diese Fläche berechnen zu können, wird die erste Voraussetzung der Integralrechnung benötigt: die Stammfunktion.
Und wir verraten dir jetzt wie man diese bildet.
Stammfunktion bilden
Jede differenzierbare Funktion F, für die gilt: die Ableitung von F(x) ist f(x), heißt Stammfunktion von f.
Die Stammfunktion wird dabei mit F(x) angegeben.
F´(x) = f(x) für alle x aus dem gemeinsamen Definitionsbereich von f und F.
Was genau macht man beim integrieren?
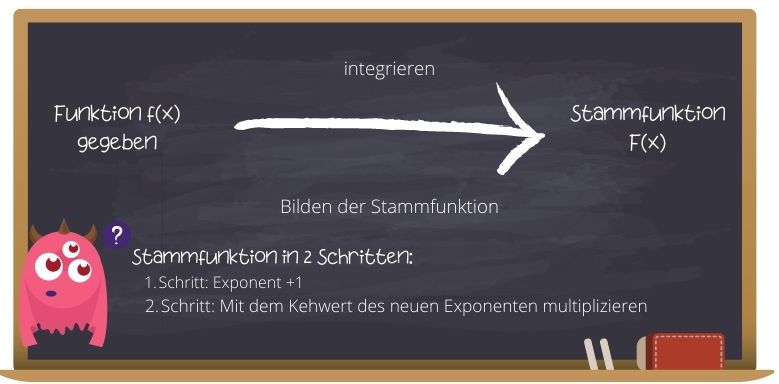
Integrieren bedeutet eine Stammfunktion zu bilden.
Die Stammfunktion berechnet man in 2 Schritten:
1. Schritt: Addiere dem Exponent +1 auf
2. Schritt: Multipliziere mit dem Kehrwert des neuen Exponenten
Beispiele zur Bildung von Stammfunktionen
Hier findest du erste Beispiele zur Berechnung der Stammfunktion F(x).
Probiere es nun selbst: Bilde die Stammfunktion bei diesen Übungsaufgaben und wähle die richtige Antwort aus.
Ergebnisse
#1. f(x)=3x³-2x
#2. f(x)=0
#3. Noch eine schwierige Aufgabe zum Schluss: f(x)=3x² - 5/x²
F(x)=6x² – 5x<sup>-2</sup>
Unbestimmtes Integral- Was bedeutet die Konstante c?
Das unbestimmte Integral lässt sich am besten durch das folgende Beispiel erklären:
Was bedeutet das?
Es gibt viele Stammfunktionen, die sich durch die Konstante c unterscheiden. Eine Funktion hat somit eine unendliche Anzahl an Stammfunktionen.
Die Menge aller Stammfunktionen einer Funktion f(x) nennt man unbestimmtes Integral der Funktion f(x).
Für die richtige Schreibweise brauchst du folgende Komponenten:
∫f(x) dx = F(x) + c Beispiel: ∫x² dx = 1/3 x³ + c
f(x)= Integrant
x = Integrationsvariable
c = Integrationskonstante
dx = Differenzial
Bestimmtes Integral- Flächenberechnung ganz leicht
Das bestimmte Integral entspricht der Fläche zwischen Funktion und x-Achse in einem gegebenen Intervall.
Für die richtige Schreibweise brauchst du folgende Komponenten:
a∫b ƒ(x) dx
a= untere Grenze
b= obere Grenze
Daraus ergibt sich der Hauptsatz der Integralrechnung:
a∫b ƒ(x) dx= F(b) – F(a)
Hauptsatz der Integralrechnung- So wendest du ihn richtig an
Um eine Integralrechnung durchzuführen und damit den Flächeninhalt in einem Intervall zwischen der unteren Grenze a und der oberen Grenze b zu berechnen, folgt man diesen Schritten:
1. Schritt: Bilden der Stammfunktion von der Funktion f(x)
2. Schritt: Einsetzen der oberen Grenze für alle x in die Stammfunktion (F(b))
3. Schritt: Einsetzen der unteren Grenze für alle x in die Stammfunktion (F(a))
4. Schritt: F(b) – F(a)
5. Schritt: Du erhältst Flächeninhalt A als Ergebnis
Das kannst du dir mit diesem Beispiel vorstellen:
Gegeben ist die Funktion f(x)= 3x² und die Grenzen a=1 und b=3.
Schritt 1: Bilden der Stammfunktion:
A=1∫3 3x² dx= [x³]
Schritt 2: Einsetzen der oberen Grenze für alle x in die Stammfunktion
F(b)= 3³
Schritt 3: Einsetzen der unteren Grenze für alle x in die Stammfunktion
F(a)= 1³
Schritt 4: F(b)-F(a)
= 3³ – 1³ = 27 – 1
Schritt 5: Ergebnis A in Flächeneinheiten
A= 26 FE
Beispiel: Berechnung von Variablen
In einigen Fällen der bestimmten Integrale besteht auch die Möglichkeit, dass einer der Grenzwerte nicht gegeben ist oder eine weitere Variable in der Funktion auftaucht und diese berechnet werden muss.
Für diese Rechnung ist in der Regel der Flächeninhalt gegeben, aber das Vorgehen bleibt im Prinzip gleich. Das einzig Neue ist die Umstellung der Gleichung nach dem unbekannten Grenzwert bzw. nach der unbekannten Variable.
Wie sieht das aus?
Probiere es selbst aus und bearbeite die folgenden Übungsaufgaben!
Gegeben ist die Funktion f(x)= x-2 mit den Grenzen a=1 und b=k und dem Flächeninhalt 3/2, sodass die folgende Gleichung entsteht:
1∫k x-2= 3/2
Aufgabe: Finde die obere Grenze k.
Lösung:
Schritt 1: Bilden der Stammfunktion
1∫k x-2= 3/2 = [½ x² – 2x]1k
2.+3. Schritt: Einsetzen der oberen und unteren Grenzen für alle x
3/2= (½*k² – 2*k)-(½*1² – 2*1)
4. Schritt: Klammern auflösen
3/2= ½*k² – 2*k + 1,5 /-3/2
5. Schritt: Subtrahieren des Flächeninhalts und anschließend Nullstellen berechnen
0= ½*k² – 2*k
Wichtig zur Berechnung der Nullstellen:
Eine genaue Anleitung zur Berechnung von Nullstellen findest du hier.
Gegeben ist die Funktion f(x)= x² + k, mit den Grenzen a=0, b=3 und dem Flächeninhalt A=15, sodass die folgende Funktion entsteht:
15=0∫3 x² + k dx= [1/3 x³ + k*x]0³
Lösung:
Schritt 1: Bilden der Stammfunktion
15=0∫3 x² + k dx= [1/3 x³ + k*x]03
2.+3. Schritt: Einsetzen der oberen und unteren Grenze für alle x
15= (9+3k) – (1/3 * 0³ + k * 0)
Schritt 4: Klammern auflösen und die Gleichung nach k umstellen
15= 9+3k /-9
6= 3k /:3
2= k
Interpretation: Die unbekannte Variable k=2
Flächeninhalt berechnen- Schritt für Schritt
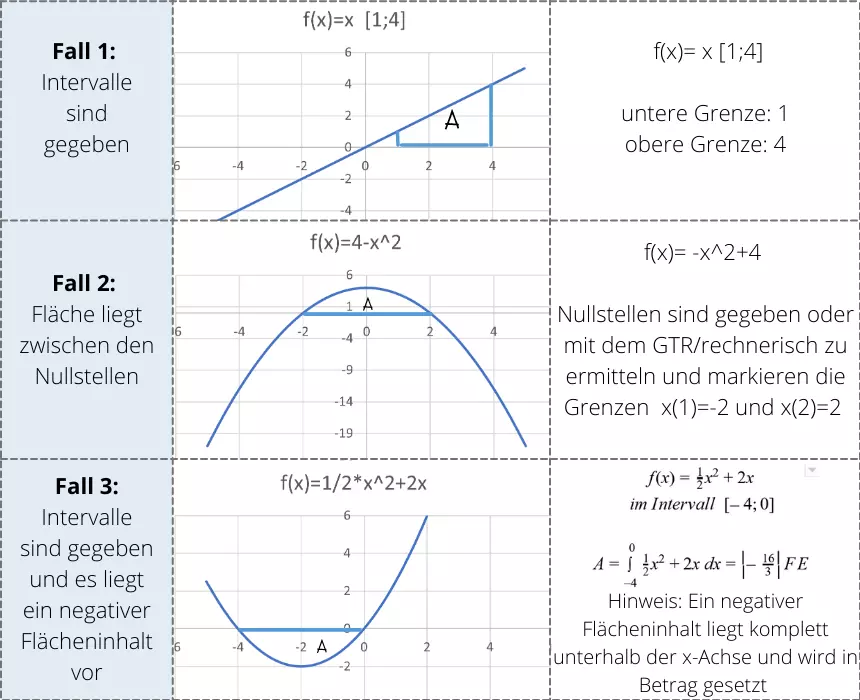
Durch das bestimmte Integral kann der Flächeninhalt in einem Intervall berechnet werden. Dabei gibt es 3 unterschiedliche Sachverhalte in der Flächenberechnung:
Beispiel: Fläche liegt komplett auf einer Seite der x-Achse
Merke: Wenn die zu berechnende Fläche komplett auf einer Seite der x-Achse liegt, sind bei der Integralrechnung 3 Fälle zu beachten:
Beispiel: Fläche liegt teilweise oberhalb und teilweise unterhalb der x-Achse
Merke: Liegt die zu berechnende Fläche teilweise oberhalb und teilweise unterhalb der x-Achse, so muss sie beim berechnen in Teilflächen zerlegt werden. Die Teilflächen werden einzeln berechnet und anschließend addiert.
Hinweis: Zur Veranschaulichung der Aufgaben kannst du dir die Funktion als ersten Schritt in deinem Graphischen Taschenrechner anzeigen lassen.
 |  |
Beispiel: Fläche zwischen zwei Funktionsgraphen
Merke: Liegen mehrere Funktionsgraphen vor, welche sich schneiden, so ergeben sich die Integralgrenzen durch die Schnittpunkte der Funktionen. Die eingeschlossene Fläche zwischen den Funktionsgraphen kann somit berechnet werden.
Um diesen Flächeninhalt zu berechnen, bieten sich 2 Möglichkeiten:
Vorgehen: Den Flächeninhalt im Intevall für jede Funktion einzeln berechnen und anschließend subtrahieren
Beispiel:
Gegeben sind 2 Funktionen im Intervall [0;1]
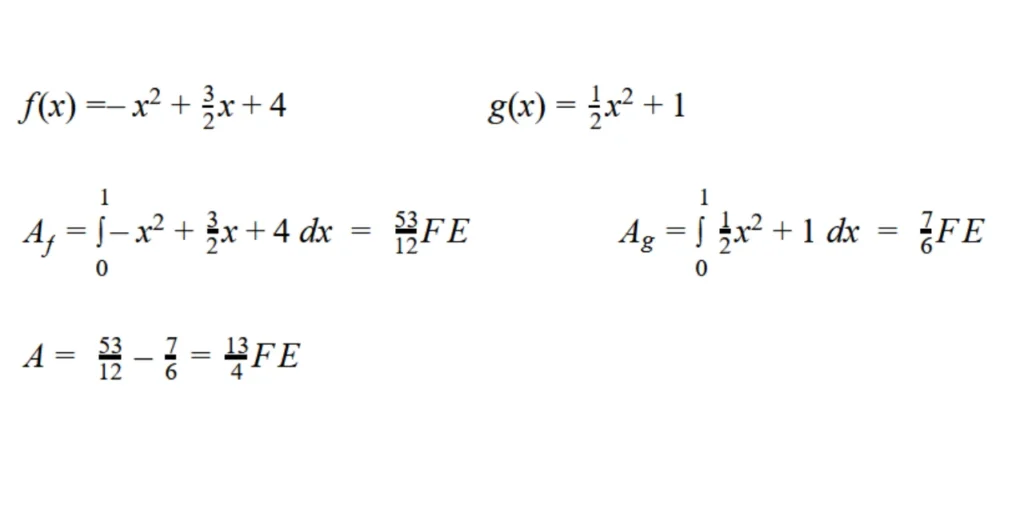
Vorgehen: Differenzfunktion
Die Differenzfunktion lässt sich mit folgender Formel darstellen:
A= a∫b f(x) – g(x) dx
Beispiel:
Gegeben sind 2 Funktionen mit den Schnittstellen x(1)= -1 und x(2)= 2
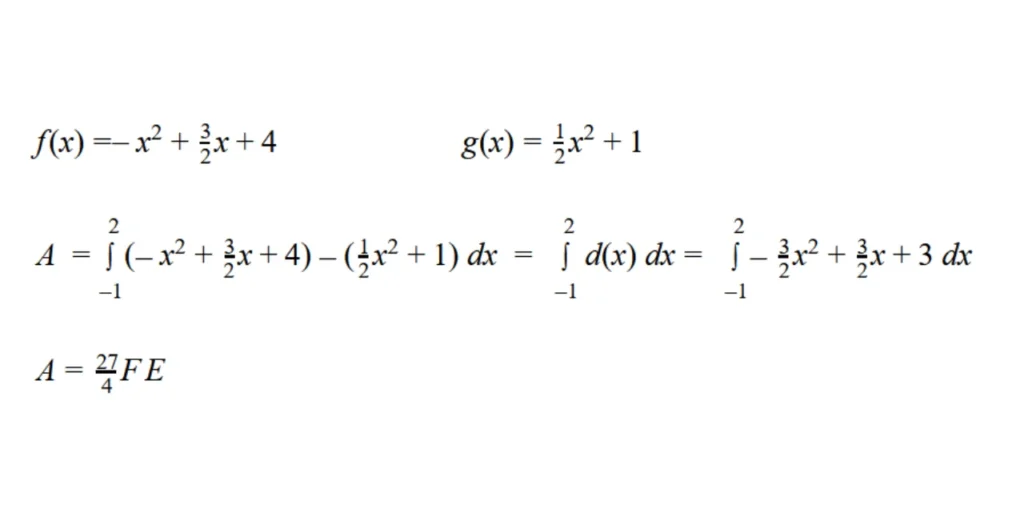
Beachte: Wenn die x-Achse in diesem Fall die Fläche teilt nimmt das keinen Einfluss auf die Berechnung!
Treten mehr als 2 Schnittstellen auf, erfolgt die Berechnung nur zwischen 2 Schnittpunkten und die Gesamtfläche ist die Summe der Teilflächen (A= A1+A2+A3+…+An= FE)
Integrale spezieller Funktionen- diese Tipps solltest du kennen
e-Funktion
Die natürliche Exponentialfunktion besteht aus der eulerschen Zahl e als Basis und dem Exponenten.
Aber wie bildet man bei der e-Funktion die Stammfunktion?
Stammfunktion bilden
Prinzipiell lautet die Regel hier:
f(x)=ex F(x)=ex f′(x)=ex
Wie du siehst bleibt die Basis erhalten. Etwas kniffliger wird es erst du die Exponenten. Dafür haben wir dir hier einige Beispiele zum Verständnis zusammengetragen.
Beispiel zur Integralrechnung bei e-Funktionen
Logarithmusfunktion
Als Logarithmusfunktion wird die Umkehrfunktion der Exponentialfunktion verstanden.
Stammfunktion bilden
Die Formel der Logarithmusfunktion lautet wir folgt:
f(x)= 1/x F(x)= ln x
Beispiel zur Integralrechnung bei Logarithmusfunktionen
Auch hier haben wir dir einige Beispiele zum Üben in einer Tabelle dargestellt.
Sinusfunktion
Die Sinusfunktion ist eine der trigonomischen Funktionen. Das Integral wird gebildet durch die negative Kosinusfunktion + Integrationskonstante c.
Stammfunktion bilden
Die Formel der Sinusfunktion lautet:
f(x)= sin x F(x)= ∫sin x dx = -cos x + c
Beispiele zur Integralrechnung bei Sinusfunktionen
Hier die Beispiele zur Bildung der Stammfunktion bei Sinus & Kosinus.
Integrationsregeln – Partielle Integration, Substitutionsmethode und Co.
Hier findest du die wichtigsten Rechenregeln in der Integralrechnung und die dazugehörigen Formeln aufgelistet.
Summenregel
Summen summandenweise integrieren:
Formel Summenregel
∫f(x) + g(x) dx= ∫f(x) dx + ∫g(x) dx
Als eine der Grundregeln der Differentialrechnung gibt die Summenregel an, dass die Summe von Funktionen integriert werden kann, indem man jede Funktion für sich integriert und die Integrationen anschließend addiert.
Faktorregel
Konstante Faktoren vor das Integral stellen:
Formel Faktorregel
∫a*f dx = a* ∫f dx
Bei der Faktorregel bleibt ein konstanter Faktor beim Aufleiten unverändert.
Partielle Integration
Formel Partielle Integration
∫f(x) * g′(x) dx = f(x) * g(x) – ∫f′(x) * g(x) dx
Die partielle Integration kann als Pendant zur Produktregel bei der Ableitung betrachtet werden. Sie wird verwendet, um eine Funktion mit zwei oder mehreren Faktoren zu integrieren.
Dabei kannst du dir aussuchen, welcher der Faktoren f(x) und welcher g(x) sein soll.
Beispiel zur Partiellen Integration
Die folgende Funktion ist gegeben und soll integriert werden:
∫2x * sin(x) dx
Schritt 1: Festlegen von f(x) und g(x)
Laut unserer Formel wird f(x) abgeleitet und g(x) im Folgenden integriert. Nach dieser Regelung legen wir den jeweiligen Faktor so fest, dass wir jeweils die einfachere Operation wählen.
Daher bestimmen wir in diesem Fall:
f(x)= 2x und g′(x)= sin(x)
Schritt 2: Ableitung und Stammfunktion bilden
f(x)= 2x f′(x)= 2
g′(x)= sin(x) g(x)= -cos(x)
Schritt 3: Formel der Partiellen Integration anwenden
∫2x * sin(x) dx= ∫f(x) * g′(x) dx = f(x) * g(x) – ∫f′(x) * g(x) dx
= -2x * cos(x) – ∫2 * (-cos(x)) dx
= -2x * cos(x) + 2 sin(x) + c
Substitutionsmethode
Formel Substitutionsmethode
∫f(g(x)) * g′(x) dx = ∫ f(u) du
mit u= g(x) und du= g′(x) dx
Was bedeutet das?
Die Substitutionsmethode ist für die Integrale das, was bei den Ableitungen der Kettenregel entspricht. Man benötigt sie bei verketteten Funktionen, wobei ein Teil der Funktion substituiert bzw. ersetzt wird.
Beispiel zur Substitutionsmethode
Die folgende Funkion ist gegeben und soll berechnet werden:
∫e4x dx
Schritt 1: Vorbereitung Substitution
Wie bereits bei der Übersicht der e-Funktion angemerkt, bleibt die e-Funktion selbst beim Bilden der Stammfunktion gleich. f(x)= ex F(x)=ex +c
In der Aufgabe ist jedoch im Exponent 4x gegeben. Daher wird bei der Substitutionsmethode zunächst der Exponent für die Variable u ersetzt
⇒ 4x = u
Anschließend wird diese Gleichung nach x aufgelöst:
⇒ x= ¼ * u
Da nach der Formel u=g(x) bedeutet das: g(x)= ¼ u
Du hast es fast geschafft! Es sind nur noch wenige Schritte bei der Substitutionsmethode! Für die Formel benötigst du noch die Ableitung deiner gerade aufgestellten Gleichung.
g′(x)= ¼
Perfekt! Somit kannst du jetzt die Integrationsvariable ersetzen: du= ¼ * dx
Schritt 2: Substitution
Jetzt erfolgt die eigentliche Substitution F(x)=e4x dx mit 4x= u und du= ¼dx
Daraus folgt: F(u)=∫eu * ¼ dx= ¼ * ∫eu dx
Schritt 3: Integration
Nun folgt die Integration
F(u)=¼*∫eu dx = ¼* eu + c
Schritt 4: Rücksubstitution
Einsetzen von u=4x in F(u)= ¼*e4x + c
Ergebnis: F(x)= ¼*e4x + c
Zusammenfassung
Du hast bei uns gelernt:
…was eine Integralrechnung ist und mit welchen 2 Schritten eine Stammfunktion gebildet wird,
…worin der Unterschied zwischen einem unbestimmten und einem bestimmten Integral liegt,
…wie der Hauptsatz der Integralrechnung lautet: a∫b ƒ(x) dx= F(b) – F(a),
…mit der Integralrechnung den Flächeninhalt zu berechnen,
…die Stammfunktion für e-, log- und sin- Funktionen korrekt zu bilden,
…und welche Integrationsregeln es gibt und wie man sie richtig anwendet.
Ich hoffe, dir hat unser Beitrag zur Integralrechnung gefallen und du fühlst dich auf die nächste Mathestunde bestens vorbereitet!
Wir würden von dir gerne wissen: Was hat dir besonders geholfen? Und konntest du die Quizfragen richtig beantworten?
Wir freuen uns über deinen Kommentar 🙂
Unser Nachhilfe-Team findest du übrigens in ganz Deutschland und nicht nur in Großstädten, wie München, Köln oder Berlin. Unsere unschlagbaren Mathe Lehrer gibt es außerdem auch im Online Unterricht– dies ist die beliebteste Option unserer Nachhilfeschüler.
Für dich könnte weiterhin nützlich sein:
- Flächeninhalt berechnen – alle Rechenwege im Überblick
- Kurvendiskussion – Rechenbeispiele und schnellste Wege