4,29 von 5 Sterne
Loading...
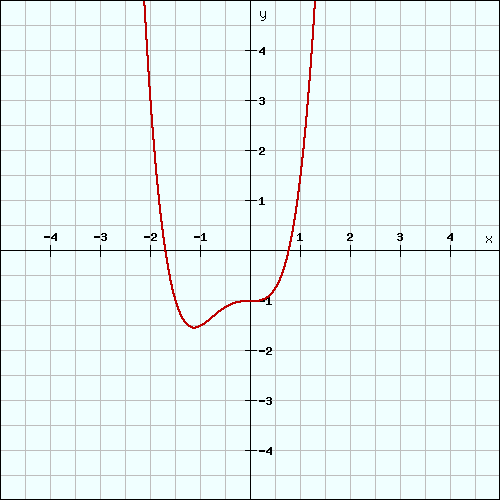
Du musst bestimmte Eigenschaften einer ganzrationalen Funktion ermitteln, du weißt aber nicht, wie du vorgehen sollst?
Wir zeigen dir hier:
- welche Grenzverhalten ganzrationale Funktionen aufweisen
- die Symmetrieeigenschaft ganzrationaler Funktionen
- wie du die Nullstellen der Funktion berechnest
- wie du Extremstellen bestimmen kannst
- worauf du bei den unterschiedlichen Graden der Funktionen achten musst.
Lass uns loslegen!
Eigenschaften ganzrationaler Funktionen – Eine Übersicht
Eine ganzrationale Funktion n-ten Grades ist eine Funktion der Form
Die Zahlen vor den Potenzen werden Koeffizienten genannt. Eine Ausnahme stellt die Zahl vor der höchsten Potenz dar. Dieser wird als Leitkoeffizient bezeichnet.
Der höchste Exponent bestimmt den Grad der Funktion. Ist dieser zum Beispiel eine 3, ist die ganzrationale Funktion eine Funktion 3. Grades
Funktionen können hinsichtlich mehrerer Eigenschaften untersucht werden. Dazu zählen das Grenzverhalten, die Nullstellen, die Extremstellen und die Symmetrieeigenschaft. Diese Eigenschaften untersuchen wir jetzt bei jeder Polynomfunktion.
Das Grenzverhalten rationaler Funktionen
Das Grenzverhalten beschreibt, wie eine Funktion verläuft, wenn man sehr hohe bzw. sehr niedrige Werte für x einsetzt. Dabei spielen zwei entscheidende Faktoren eine Rolle. Zum einen der höchste Exponent der Funktion, sowie das Vorzeichen des Leitkoeffizienten.
Gerader Grad
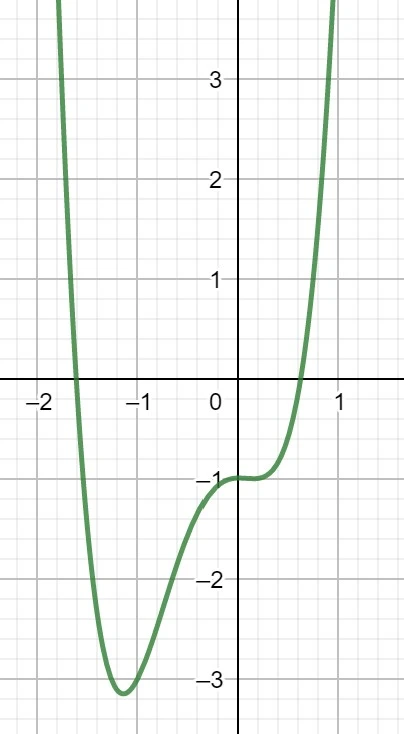
Funktionen mit einem geraden Exponenten verlaufen global betrachtet ähnlich wie eine quadratische Funktion. Dabei spielt nur der Grad des höchsten Exponenten eine Rolle.
Der Grad der anderen Exponenten ist bei der Bestimmung der Anzahl an Nullstellen relevant. Dabei gibt es zwei Möglichkeiten:
Hat der Leitkoeffizient ein positives Vorzeichen, ist die Parabel nach oben geöffnet.
und 
Dies bedeutet, dass die Funktion gegen + unendlich verläuft, wenn du sehr hohe Werte oder sehr niedrige Werte für x einsetzt.
Hat der Leitkoeffizient ein negatives Vorzeichen, ist die Parabel nach unten geöffnet.
und 
Zum Beispiel: f(x) = x4 + 3x2 + 2
Ungerader Grad
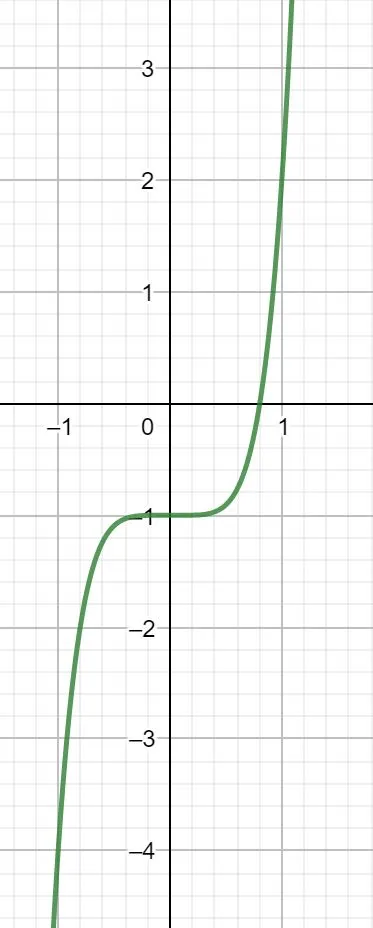
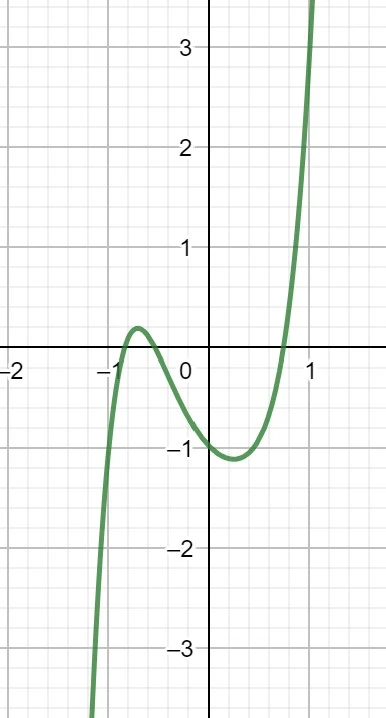
Funktionen mit einem ungeraden Exponenten verlaufen global betrachtet ähnlich wie eine Funktion 3. Grades, wobei das Vorzeichen des Leitkoeffizienten auch hier das Globalverhalten bestimmt.
Hat der Leitkoeffizient ein positives Vorzeichen:
und 
Hat der Leitkoeffizient ein negatives Vorzeichen:
und 
Zum Beispiel: f(x) = 3x5 – 4x3 + 2x
Nullstellen bestimmen
Bei der Bestimmung von Nullstellen müssen wir immer die passende Formel je nach Grad der Funktion auswählen.
Das Prinzip ist aber immer dasselbe. Wir suchen den x-Wert, bei dem f(x) = 0 gilt.
Im Allgemeinen gilt, dass eine ganzrationale Funktion maximal so viele Nullstellen besitzt, wie der Grade der Funktion ist.
Das bedeutet, dass eine Funktion 2. Grades maximal 2 Nullstellen besitzen kann. Es ist auch möglich, dass sie nur eine oder gar keine Nullstelle besitzt.
Lineare Funktionen
Bei linearen Funktionen können wir den Term f(x) = 0 einfach nach x auflösen.
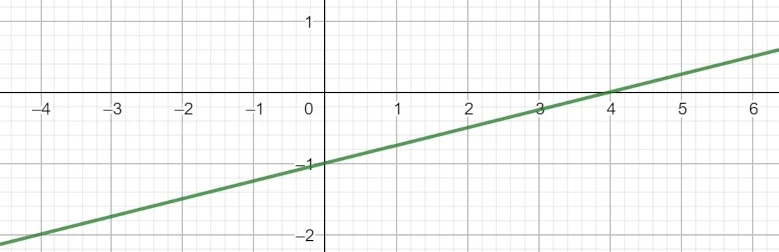
Zum Beispiel: f(x) = 2x + 4
f(x) = 0
2x + 4 = 0 |-4
2x = -4 |:2
x = -2
Die Nullstelle der Funktion liegt bei ( -2 | 0 )
Ganzrationale Funktion 2. Grades
Bei Funktionen 2. Grades, können wir nicht mehr so einfach den Funktionsterm gleich 0 setzen. Um die Nullstellen zu berechnen brauchen wir die pq-Formel oder die Mitternachtsformel.
pq-Formel: 
Dabei lautet die allgemeine Funktionsgleichung f(x) = x2 + px + q = 0
Wir müssen bei der Verwendung dieser Formel darauf achten, dass keine Zahl vor dem x2 stehen darf.
Wenn du eine Funktion gegeben hast, bei der dies nicht der Fall ist, kannst du die gesamte Funktion durch die Zahl selbst teilen.
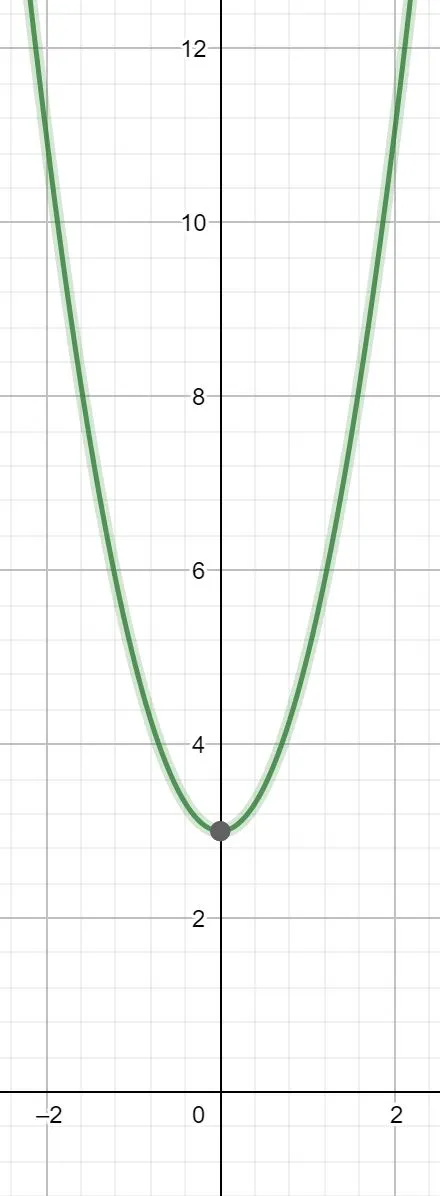
Alternativ kannst du auch die Mitternachtsformel verwenden.
Mitternachtsformel:
Dabei lautet die allgemeine Funktionsgleichung: f(x) = ax2 + bx + c = 0
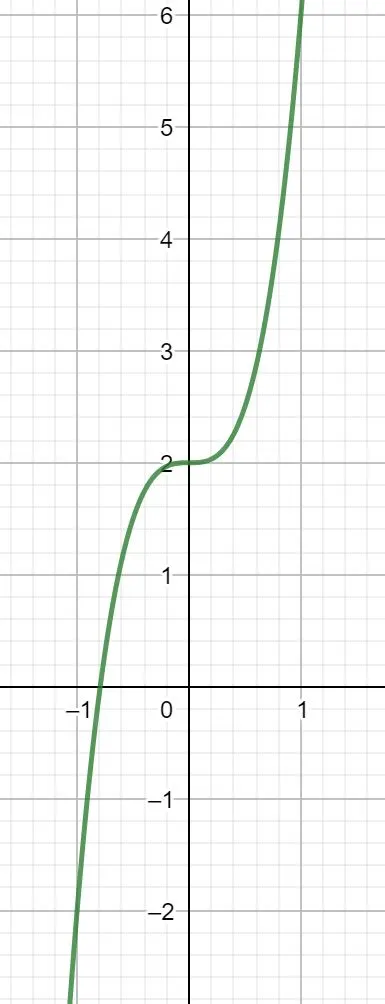
Ganzrationale Funktion 3. Grades
Bei solchen Funktionen ist die Berechnung der Nullstellen nicht mehr so einfach. Wir können mittels Ausklammern eine Nullstelle bestimmen.
Da nach dem Ausklammern der höchste Exponent 2 ist, können wir mittels der pq-Formel die restlichen Nullstellen bestimmen.
Die Extremstellen bestimmen
Bei der Bestimmung der Extremstellen spielt der Grad der Funktion keine Rolle. Das Vorgehen ist immer dasselbe.
- Schritt: Ableitung der Funktion berechnen, dazu verwenden wir die Potenzgesetze.
- Schritt: Nullstellen der Ableitung bestimmen. Dabei erhalten wir die x-Koordinaten der Extrempunkte.
- Schritt: x-Koordinaten in die ursprüngliche Funktion einsetzen, um die y-Koordinaten zu erhalten
- Schritt: Bestimmen, ob es sich um ein Minimum, Maximum oder Sattelpunkt handelt. Dies machen wir, indem wir die x-Koordinaten der Extrempunkte in die 2. Ableitung der Funktion einsetzen.
Wenn f“(x) < 0, handelt es sich um ein Hochpunkt, bei f“(x) > 0, um ein Tiefpunkt und bei f“(x) = 0 um ein Sattelpunkt.
Zum Beispiel: f(x) = 2x2 + 4x – 1
1. Ableitung bestimmen: f´(x) = 4x + 4
Nullstelle der Ableitung: f´(x) = 0
4x + 4 = 0
x = -1
f(-1) = 2 * (-1)2 + 4 * (-1) -1 = -3
2. Ableitung bestimmen f´´(x) = 4 > 0
Es handelt sich um einen Tiefpunkt an der Stelle ( -1 | -3)
Symmetrieeigenschaft ganzrationaler Funktionen
Polynomfunktionen können entweder achsensymmetrisch zur y-Achse oder punktsymmetrisch zum Ursprung sein. Dabei sind die Exponenten der Funktion entscheidend.
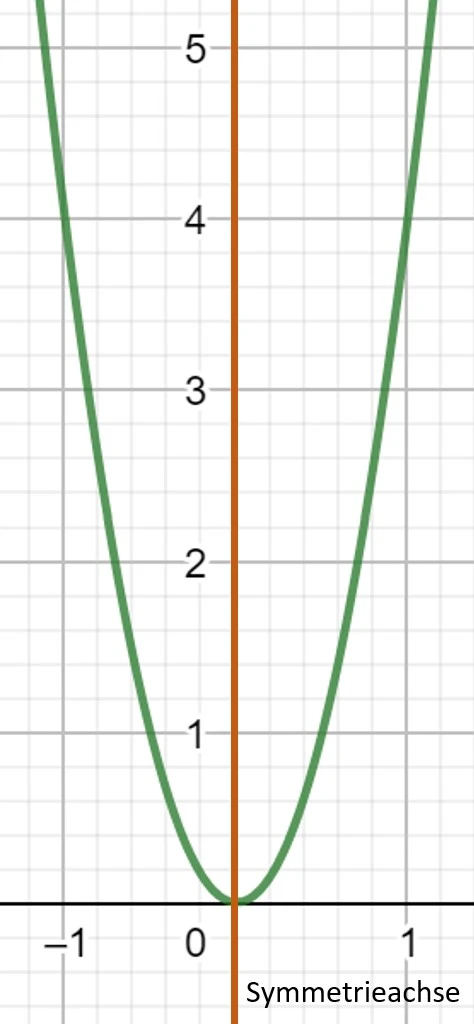
Achsensymmetrie
Eine Funktion ist achsensymmetrisch, wenn gilt: f(x) = f(-x)
Daraus lässt sich ableiten, dass ganzrationale Funktionen immer dann achsensymmetrisch sind, wenn sie nur gerade Exponenten enthalten, da sich bei geraden Exponenten alle negativen Vorzeichen umkehren.
Dabei spielt es keine Rolle, ob die Funktion eine Konstante beinhaltet, da die Konstante die Funktion lediglich nach oben bzw. unten verschiebt und somit keine Auswirkung auf die Achsensymmetrie hat.
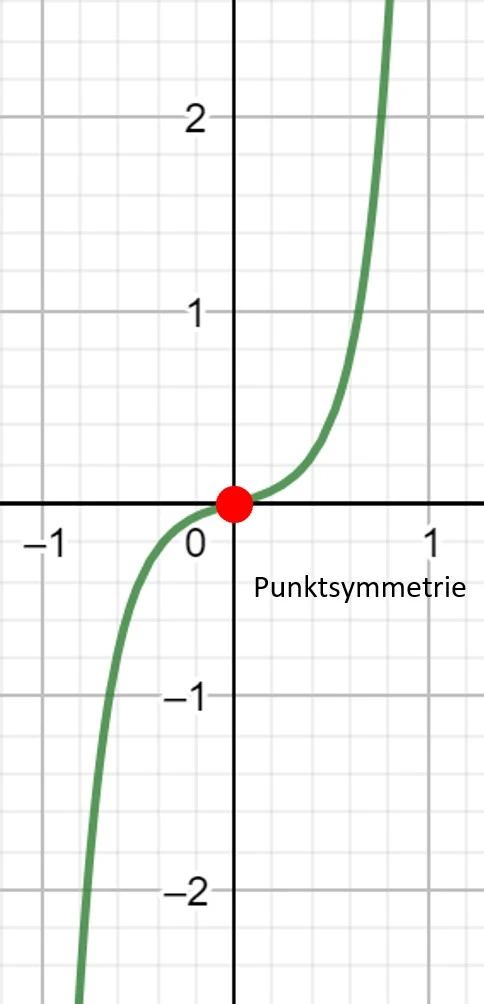
Punktsymmetrie
Die Bedingung für Punktsymmetrie ist: -f(x) = f(-x)
Das bedeutet, dass eine Funktion immer dann punktsymmetrisch zum Ursprung ist, wenn sie nur ungerade Exponenten enthält.
Dabei darf die Funktion keine Konstante haben, da sonst die Punktsymmetrie zum Ursprung nicht mehr gegeben ist.
Besitzt eine ganzrationale Funktion sowohl gerade als auch ungerade Exponenten, so ist sie weder punkt- noch achsensymmetrisch.
Ganzrationale Funktionen – FAQ
Wie kann ich den Grad einer ganzrationalen Funktion bestimmen
Der Grad einer Funktion ist immer gleich der höchsten Potenz. Beispielsweise ist die Funktion f(x) = 3x4+ 2x – 5 eine Funktion 4. Grades, da der höchste Exponent eine 4 ist.
Ist eine Parabel eine ganzrationale Funktion?
Ja, eine Parabel ist eine ganzrationale Funktion des Grades 2. Sie wird wie folgt dargestellt: f(x) = ax2+bx+c.
Ist eine Gerade eine ganzrationale Funktion?
Ja, eine Gerade ist eine ganzrationale Funktion. Sie lässt sich so darstellen: f(x) = a1 + b. Das bedeutet, die Funktion ist eine Funktion vom Grad 1.
Übungen
Ergebnisse
#1. Guck dir das Bild von dem Graphen an. Welche Funktion f(x) passt dazu?
#2. Wenn bei einer Funktion mit geradem Grad der Leitkoeffizient ein positives Vorzeichen hat,…
#3. Wie viele Nullstellen kann eine Funktion 2. Grades haben?
Hat dir der Inhalt geholfen? Lass uns gerne einen kurzen Kommentar da, wir würden uns sehr freuen! Ansonsten findest du weitere hilfreiche Erklärungen zu verschiedenen Themengebieten auf der Homepage des Nachhilfe-Teams.
Du möchtest noch besser in Mathe werden? Dann haben wir die richtige Lösung für dich!
Probiere jetzt unsere Mathe Nachhilfe aus! Denn egal wo in Deutschland – durch unsere über 800 Tutoren und unserem alternativen Online-Programm haben wir alles Nötige für deine Mathe Hilfe!