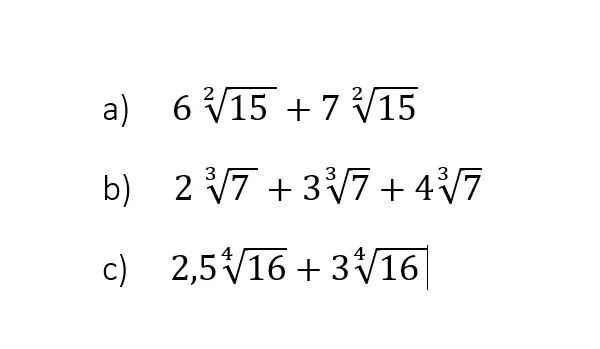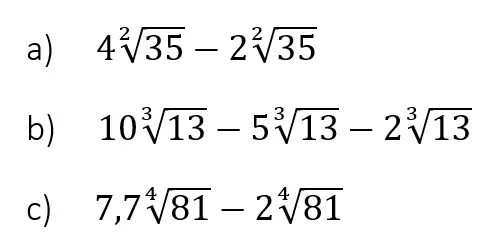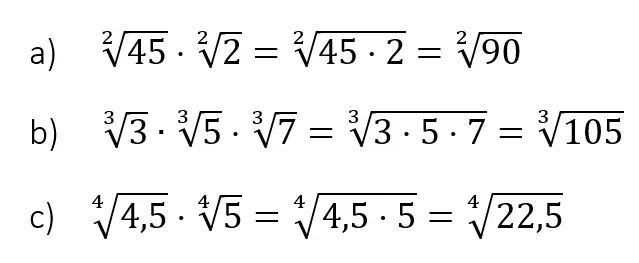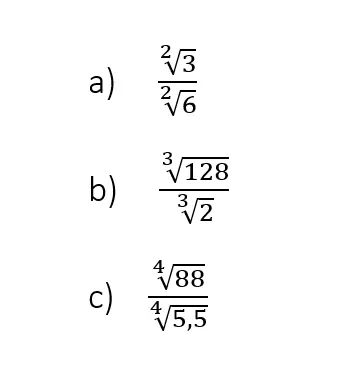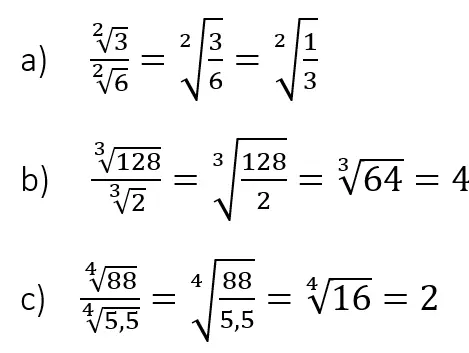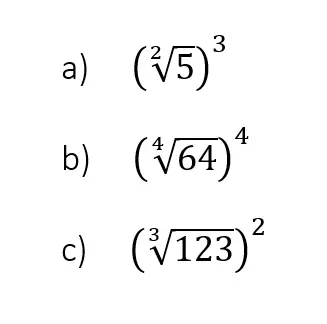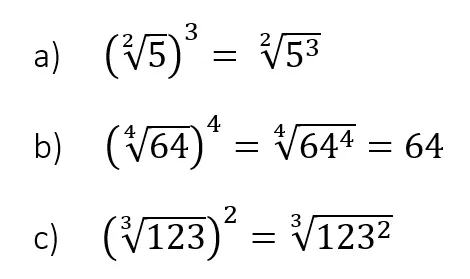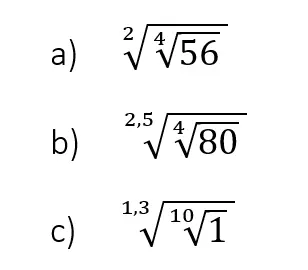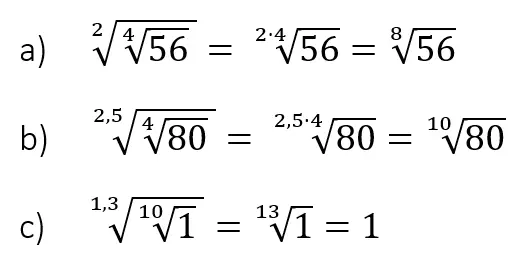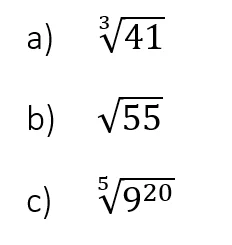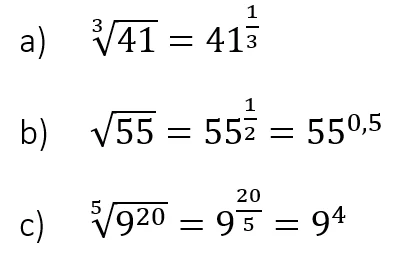Wurzelgesetze – Die 6 wichtigsten Regeln im Überblick

Häufig sollst du im Matheunterricht Wurzeln auf verschiedenste Weisen miteinander verrechnen. Doch wie funktioniert das? Wie addiere oder multipliziere ich Wurzeln miteinander?

Wir zeigen dir alle wichtigen Wurzelgesetze, die du kennen solltest. Anhand verschiedener Beispiele lernst du sie schnell zu verstehen.

Fangen wir doch direkt mit dem Aufbau einer Wurzel an! Los geht’s.

Was ist eine Wurzel und wie ist sie aufgebaut?

Zuerst stellen wir uns die Frage wie eine Wurzel aufgebaut ist. Eine Wurzel besteht aus drei Komponenten. Einmal dem Wurzelzeichen, dem Radikand und dem Wurzelexponenten. Das Ergebnis einer Wurzel wird als Wurzelwert bezeichnet.

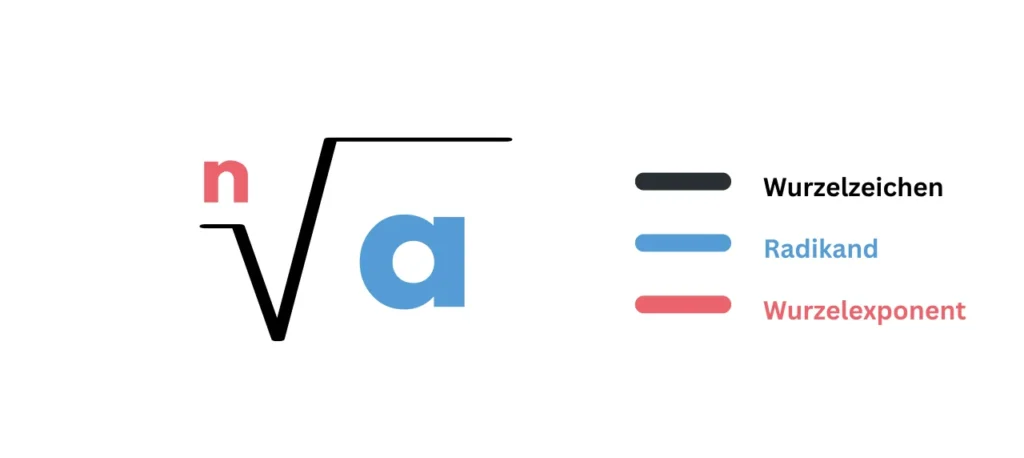
Wurzeln hängen sehr stark mit der Potenzrechnung zusammen. Denn bei einer Wurzelrechnung fragst du dich, welcher Wurzelwert n-mal mit sich selbst multipliziert, so dass es a (Radikand) ergibt.

Nehmen wir als Beispiel  ∛8. Der Wurzelwert hier ist 2, denn 2·2·2 = 4·2 = 8. Also ist ∛8 = 2.

Was du dir auf jeden Fall merken solltest ist, dass der Radikand niemals eine negative Zahl sein kann.

Quadratwurzel

Die gängigste Wurzel, die man kennt, ist die Quadratwurzel. Dass bedeutet, du ziehst die zweite Wurzel aus dem Radikanden.

Die Quadratwurzel kannst du entweder mit n = 2 darstellen oder in dem Fall kann der Wurzelexponent auch weggelassen werden.

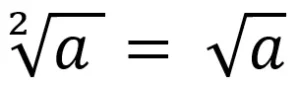
Kubikwurzel

Eine weitere Wurzelform, die dir öfters im Matheunterricht über den Weg laufen wird, ist die Kubikwurzel. Bei der ist n = 3

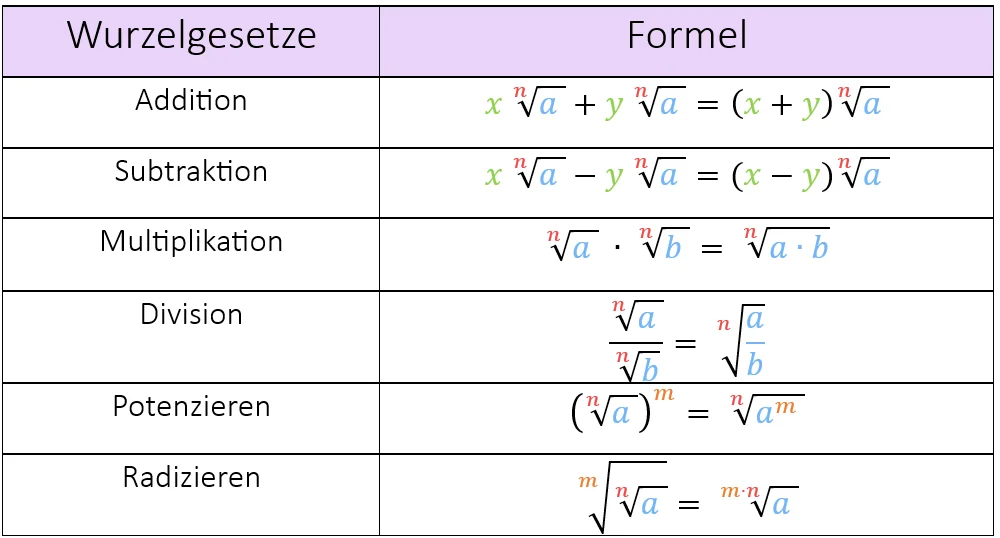
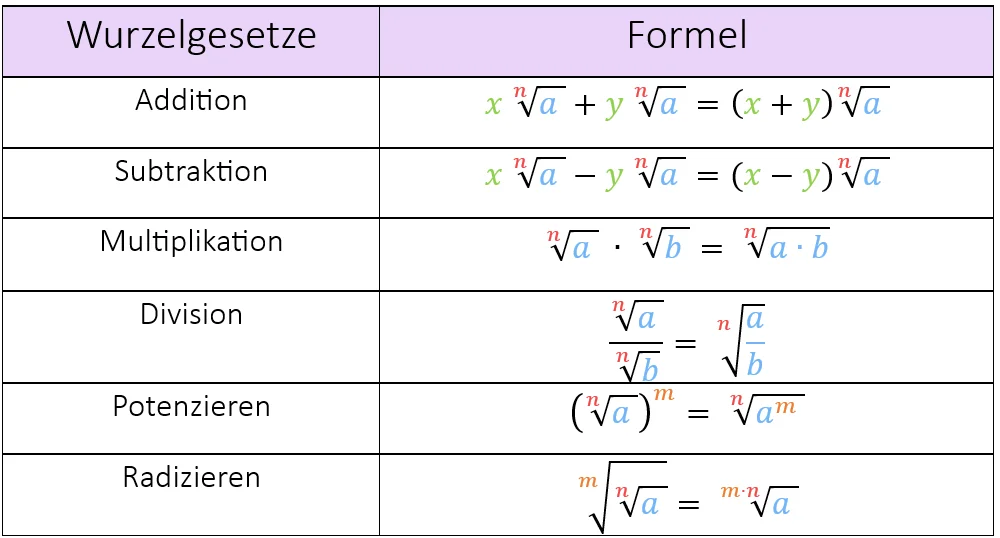
Die 6 wichtigsten Wurzelgesetze

Jetzt zeigen wir dir, welche Wurzelgesetze dir bei deinen Berechnungen weiter helfen werden. Dafür haben wir für dich hier  alle Wurzelgesetze kurz und knackig zusammengefasst.

Nach der Tabelle findest du nochmal alle Wurzelgesetze mit deren genauen Voraussetzungen und Beispielen.

Wurzelgesetz Addition

Die erste Regel, die du kennen solltest, ist das Addieren von zwei Wurzeln. Dabei müssen folgende Voraussetzungen erfüllt sein:

1. gleicher Radikand
2. gleicher Wurzelexponent

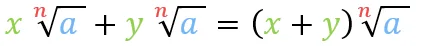
Wurzelgesetz Subtraktion

Als nächstes beschäftigen wir uns damit wie du Wurzeln voneinander subtrahierst. Wie bei der Addition gibt es auch hier bestimmte Voraussetzungen:

1. gleicher Radikand
2. gleicher Wurzelexponent

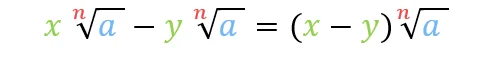
Wurzelgesetz Multiplikation

Eine weitere Grundrechenart ist die Multiplikation. Diese kann auch bei Wurzeln angewendet werden.

1. gleicher Wurzelexponent
2. unterschiedliche Wurzelexponenten => Wurzeln gleichnamig machen

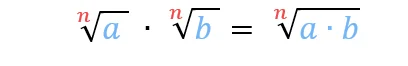
Wurzelgesetz Division

Bei der Wurzelrechnung kann es auch dazu kommen, dass du Wurzeln miteinander teilen muss. Wir zeigen dir wie es geht.

1. gleicher Wurzelexponent
2. unterschiedliche Wurzelexponenten => Wurzeln gleichnamig machen

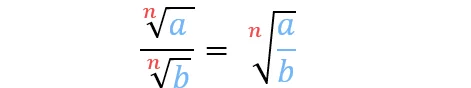
Wurzel potenzieren

Neben den Grundrechenarten hast du noch die Möglichkeit Wurzeln zu potenzieren. Hierbei gibt es keine Voraussetzungen, die du erfüllen muss.

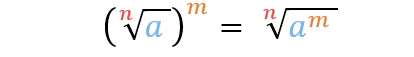
Wurzel radizieren

Wie du siehst kannst du sogar aus einer Wurzel eine Wurzel ziehen. Wir zeigen dir wir du, dass Ganze vereinfachen kannst.

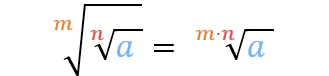
Wurzel umschreiben – in Potenzen umformen

Wusstest du eigentlich, dass du Wurzeln auch in Potenzen umformen kannst? Wie wir am Anfang erwähnt haben, hängen die Wurzelrechnung und Potenzrechnung stark zusammen.

So ist es gut zu wissen ,wie man Wurzeln richtig umformt. Denn manchmal ist es einfacher mit Potenzen zu rechnen als mit Wurzeln.

Dafür kannst du dir folgende Formel merken:

Kostenlose Übungen

Hier kannst du nochmal dein Wissen testen, ob du auch alle Wurzelgesetze drauf hast und auch weiß wie man Wurzeln richtig umformt.

FAQ – Wurzelgesetze, die meist gestellten Fragen

Wir haben für dich hier einmal alle wichtigen Punkte in Form eines FAQ zusammengefasst. Einfach auf das Plus + klicken, um die Antwort zu sehen.