Winkel Arten bestimmen: Alle Winkel im Überblick

Wie war das nochmal mit den Winkel-Arten? Du bist dir nicht sicher? Kein Problem.

Hier erfährst du …

• was ein Winkel ist
• welche Winkelarten es gibt
• was sie ausmacht
• welche Winkeltypen es gibt
• wie du mit den Typen die Gradzahlen leichter bestimmen kannst

Starten wir gleich mit dem ersten Punkt:

Was ist ein Winkel?

Er gibt an in welchem Verhältnis zwei Geraden oder Strecken aufeinander treffen. Dieses Verhältnis wird in der Einheit Grad angegeben und ist abhängig davon, in welcher Neigung die beiden Geraden zueinander stehen.

Solange zwei Geraden nicht absolut parallel zueinander verlaufen, haben sie immer einen gemeinsamen Schnittpunkt, um den herum sich ein Winkel aufspannt. Eigentlich sogar mehrere, aber dazu kommen wir später.

Winkel werden grundsätzlich immer mit den Buchstaben des griechischen Alphabets beschriftet beziehungsweise benannt. Also: α, β, γ, δ … und so weiter.

Winkelarten

In der Geometrie unterscheidet man in verschiedene Winkelarten. Jeder Winkel, den es gibt, lässt sich einer dieser Arten genau zuordnen.

Die Winkelart kann man für gewöhnlich mit bloßem Auge erkennen, ohne irgendwelche Hilfsmittel zu benötigen, weil sie von der Gradzahl abhängig ist. Wenn man sich jedoch unsicher ist, kann man ganz einfach mit einem Geodreieck oder Winkelmesser nachmessen.

(Check auch mal die Trigonometrie aus 😉 )

Nullwinkel

Ein Nullwinkel hat ganz genau 0°. Die Geraden, die ihn bilden, sind miteinander identisch, liegen also genau aufeinander. Darum ist der Teilkreis nicht sichtbar.

spitzer Winkel

Ein spitzer Winkel ist größer als 0°, aber kleiner als 90°. Man findet sie mindestens zwei von ihnen in jedem Dreieck.

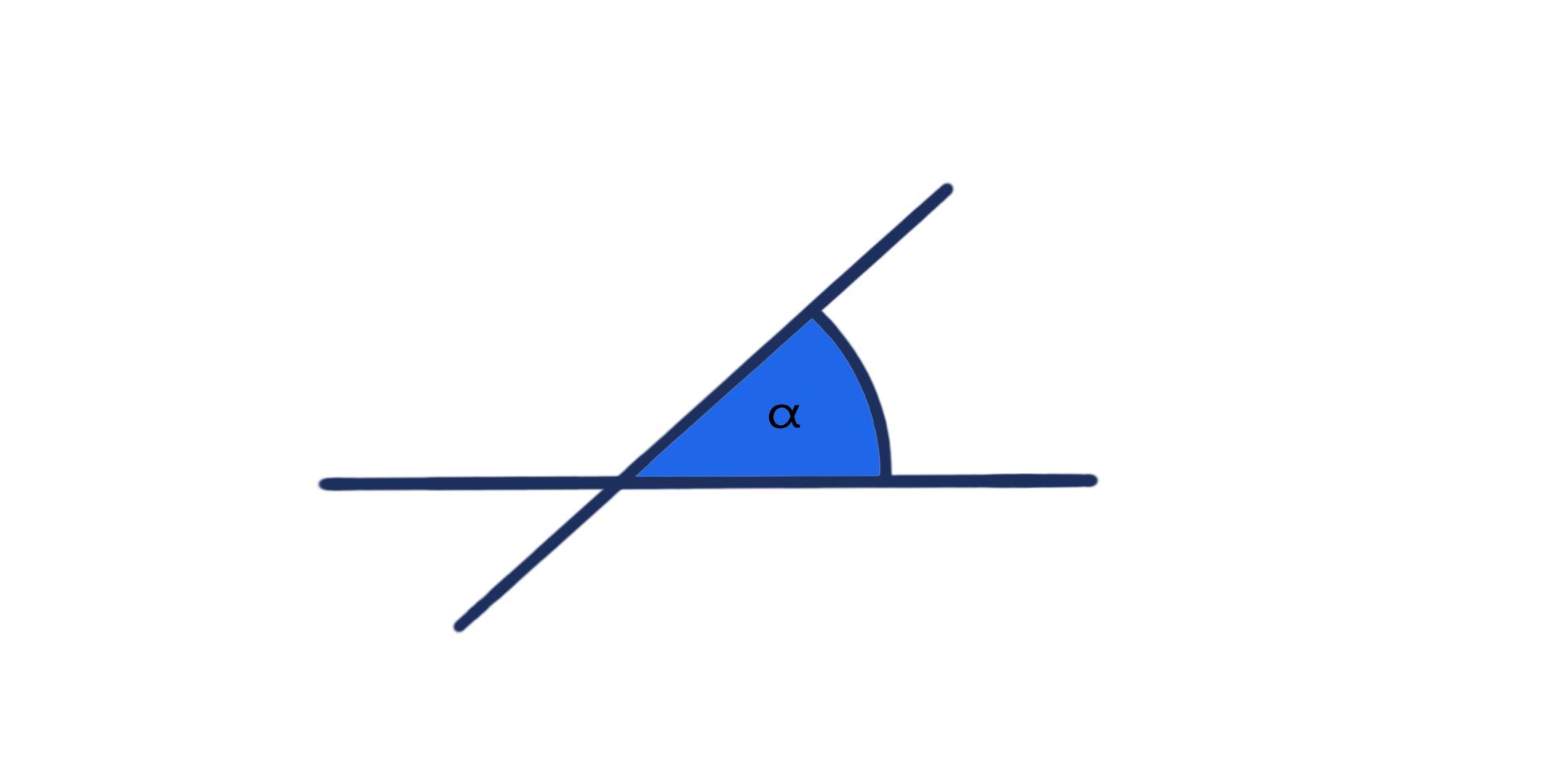
rechter Winkel

Ein rechter Winkel ist ganz genau 90° groß.
Man kennt sie aus Rechtecken, wie der Name schon vermuten lässt oder auch aus einigen besonderen Dreiecken. In geometrischen Zeichnungen werden sie oft dargestellt, indem man einfach nur einen Punkt in die Mitte des eingezeichneten Teilkreises setzt.

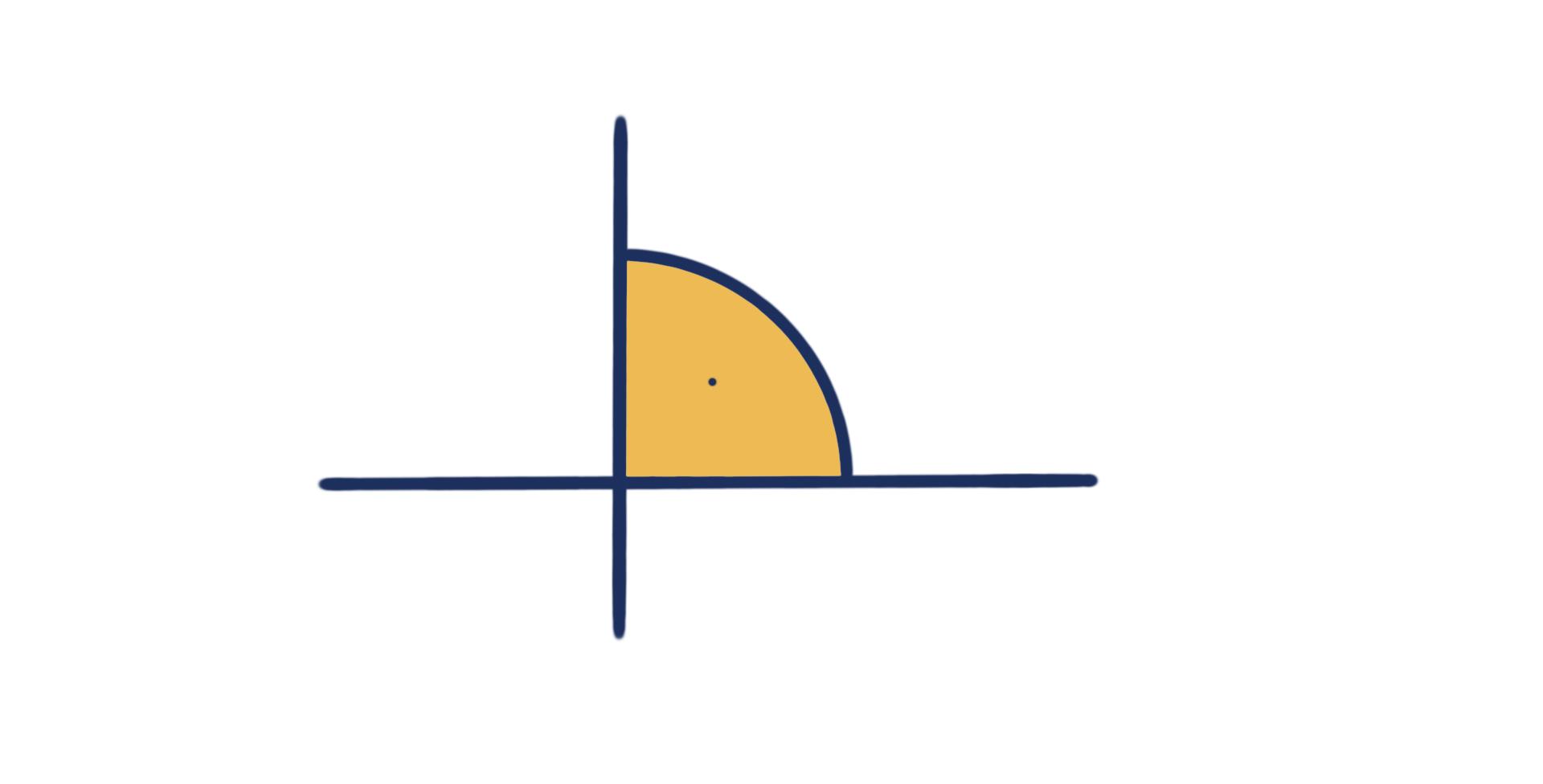
stumpfer Winkel

Ein stumpfer Winkel ist zwischen 90° und 180° groß. Winkel, die genau 90° oder 180° Grad groß sind, zählen aber natürlich nicht mehr zu ihnen.

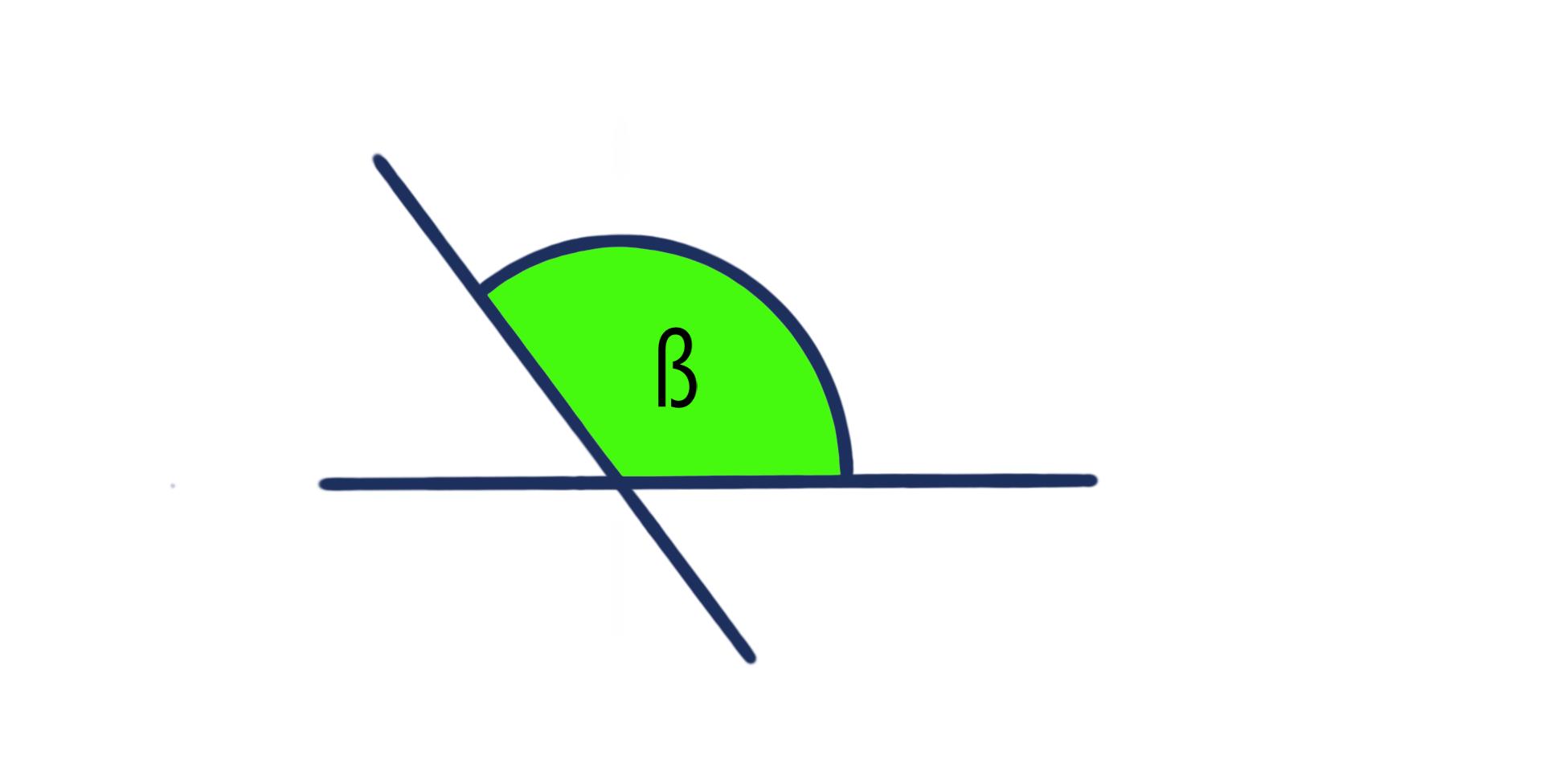
gestreckter Winkel

Ein gestreckter Winkel ist genau 180° groß.
Das Besondere an ihm ist, dass die Geraden, die ihn bilden tatsächlich parallel verlaufen, zusätzlich aber auch noch genau aufeinander liegen, also identisch sind. Dadurch wird der Teilkreis zum Halbkreis gestreckt und in der Darstellung ist nur eine einzige Gerade zu erkennen.

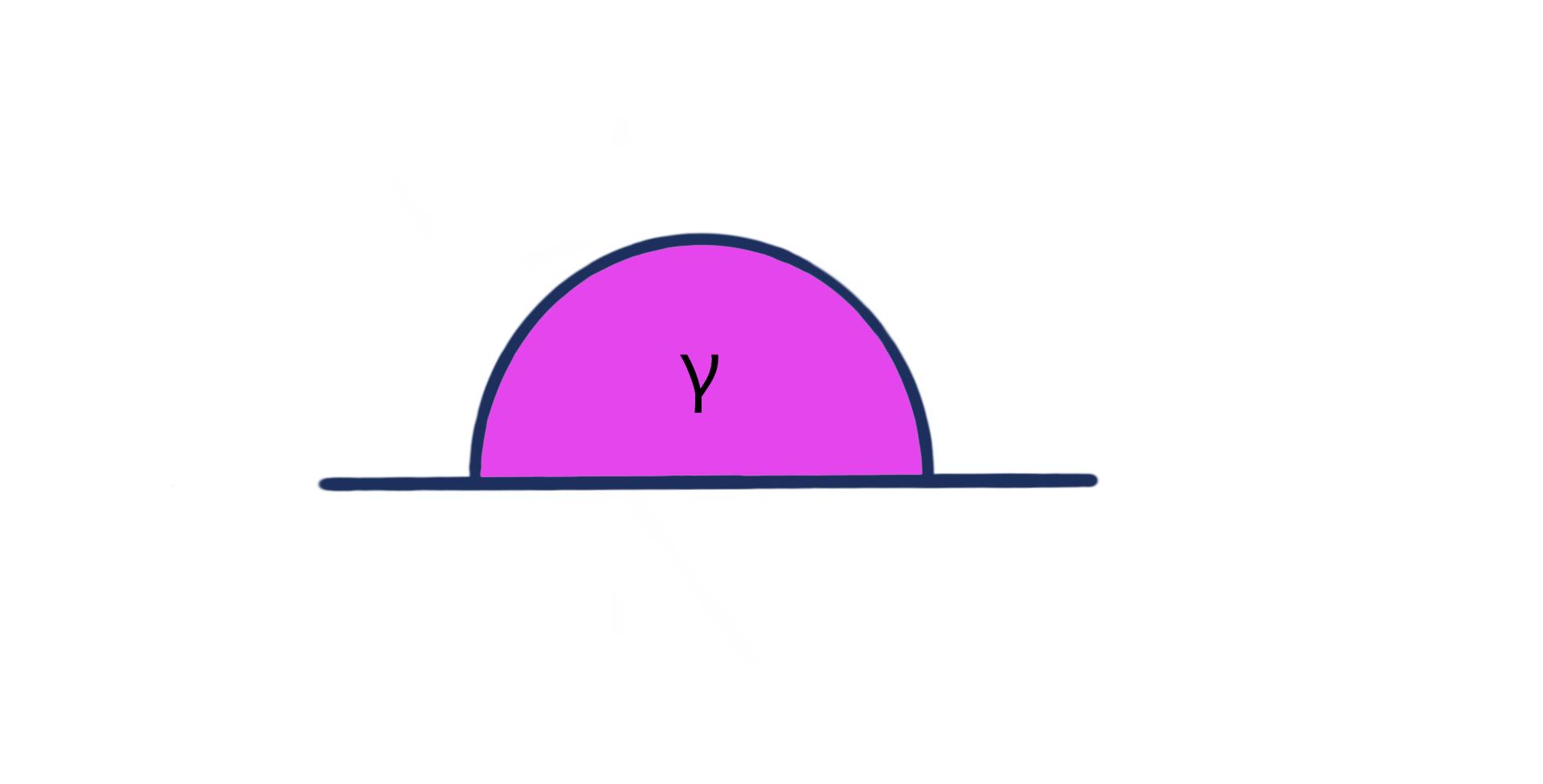
überstumpfer Winkel

Als überstumpfe Winkel bezeichnet man solche, die mehr als 180° haben. Ausgenommen sind davon allerdings jene, die genau 360° haben.

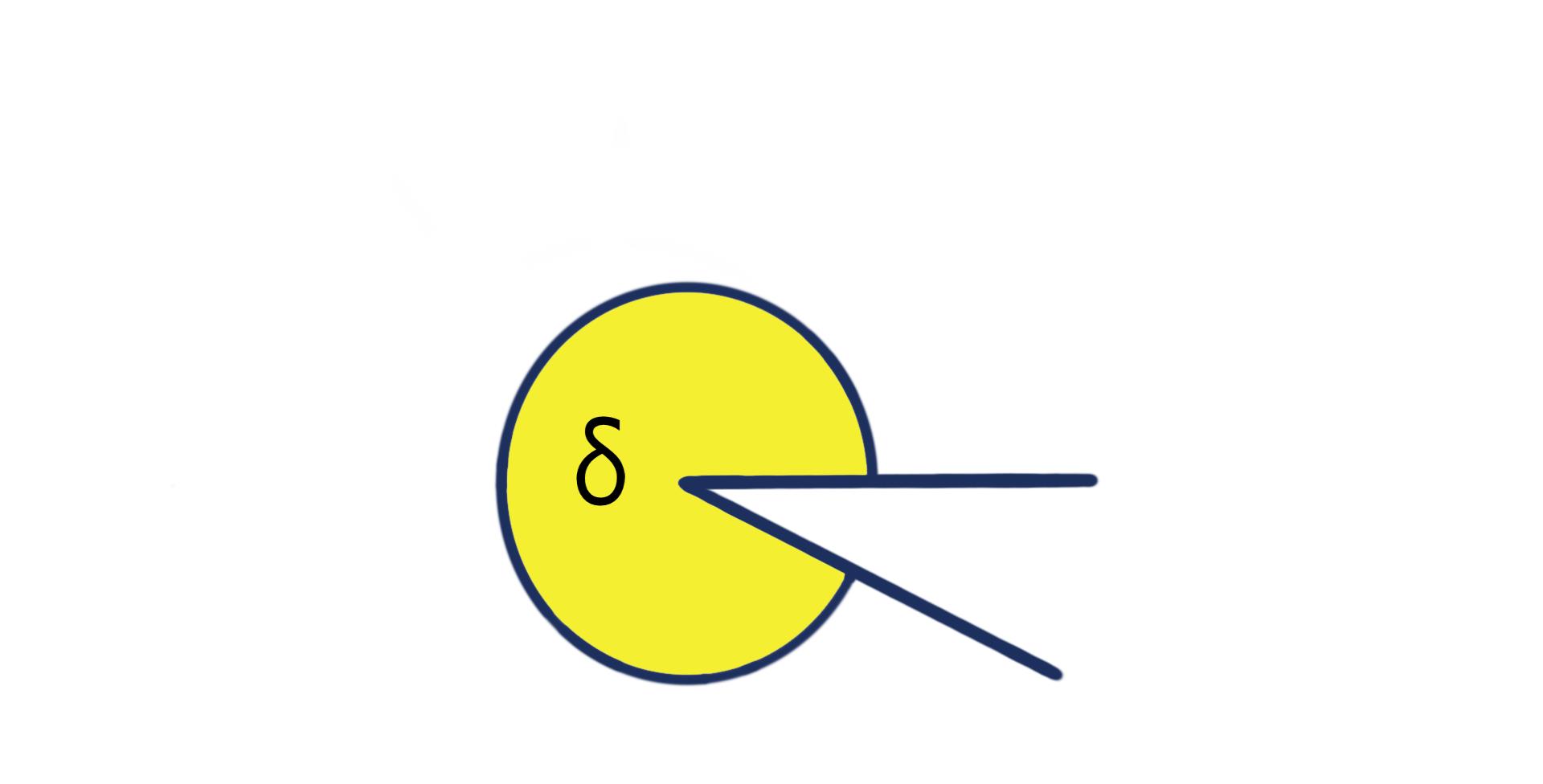
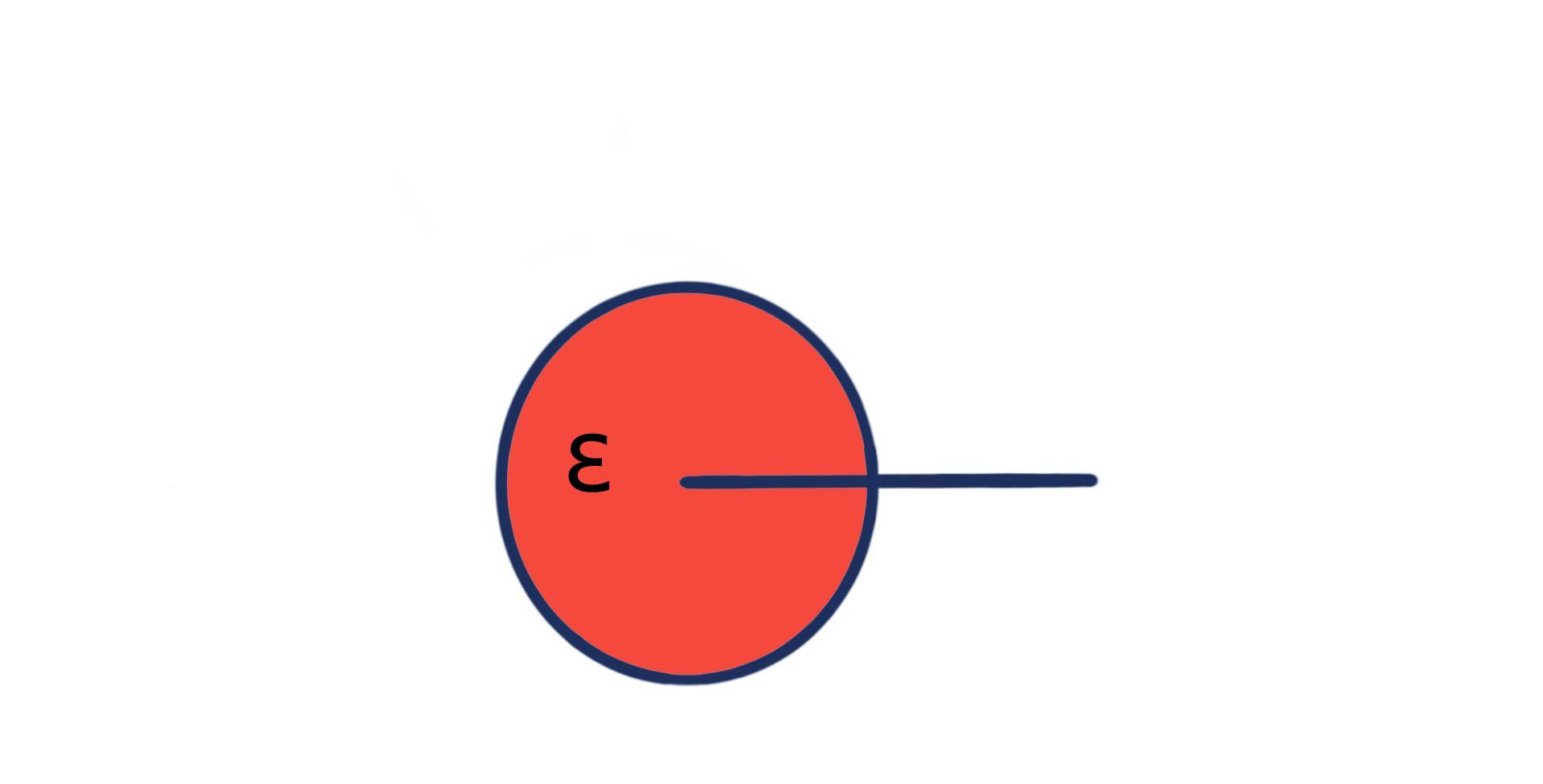
Vollwinkel

Der Vollwinkel hat immer genau 360° und stellt damit das Gegenteil zum Nullwinkel dar. In geometrischen Zeichnungen sieht er immer aus wie ein Kreis.

Winkeltypen

Wie oben bereits erwähnt, bilden Geraden, die sich schneiden, eigentlich nicht nur einen, sondern tatsächlich vier Winkel. Sie stehen zueinander in einem ganz besonderen Verhältnis und bilden ein Gefüge, das immer die gleichen Eigenschaften aufweist.

Man kann in vier Winkeltypen unterscheiden und die sehen wir uns jetzt genauer an:

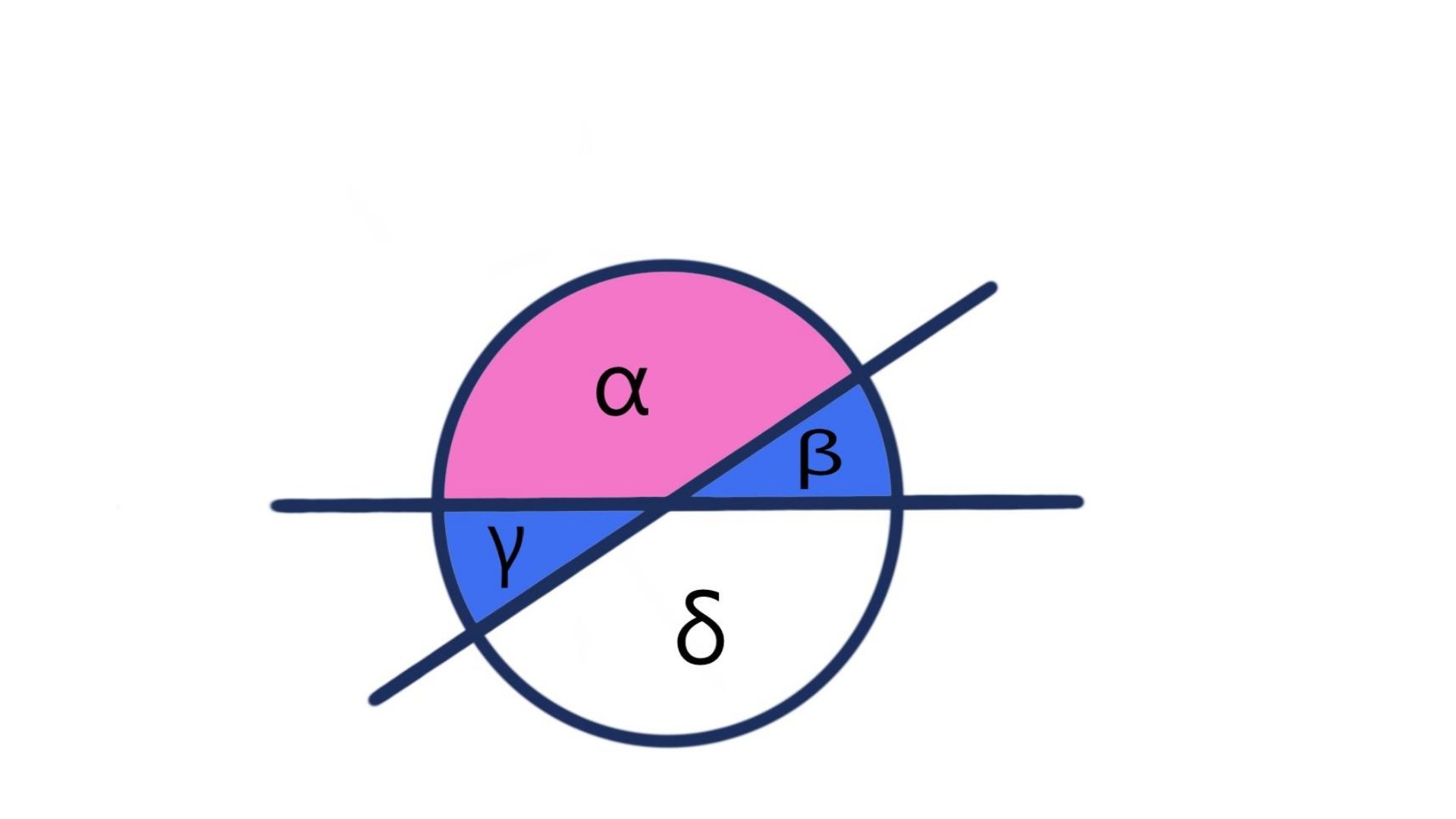
Nebenwinkel

Nebenwinkel sind solche, die direkt an den Bezugswinkel grenzen. Soll heißen, sie werden nur durch eine Gerade voneinander getrennt. Jeder Winkel hat immer zwei von ihnen.

In der unteren Abbildung sind zum Beispiel β und γ die Nebenwinkel von α.

Ein Winkel ergibt zusammen mit einem seiner Nebenwinkel immer 180°. Wenn man also weiß wie viel Grad α hat, dann kann man auch ausrechnen wie viel Grad β und γ haben.

Scheitelwinkel

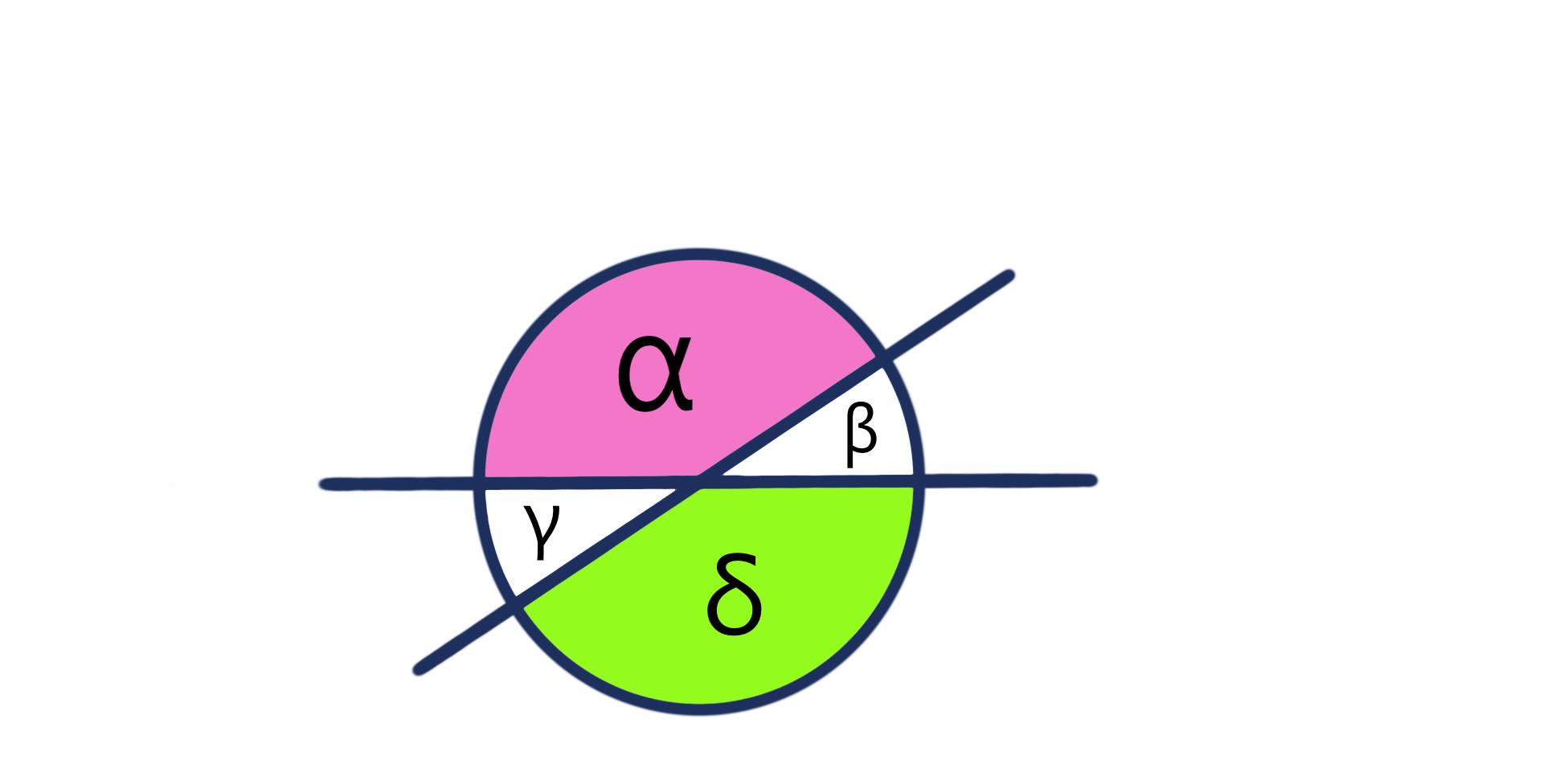
Der Scheitelwinkel liegt genau gegenüber vom Bezugswinkel. Also auf der entgegengesetzten Seite des Kreises. Jeder Winkel hat immer einen Scheitelwinkel.

In der unteren Abbildung ist δ der Scheitelwinkel von α.

Ein Winkel hat immer genauso viel Grad wie sein Scheitelwinkel. Wenn man also weiß wie viel Grad α hat, dann weiß man auch wie viel Grad δ hat.

Stufenwinkel

Jetzt sehen wir in der Abbildung unten, dass eine der Geraden entlang der anderen Gerade parallel verschoben wurde. Dadurch entsteht ein zweiter Schnittpunkt mit ebenfalls vier Winkeln. Weil eine Gerade entlang der anderen Gerade parallel verschoben wurde, werden dadurch quasi auch die exakten Gradzahlen des unteren Kreises auf den oberen Kreis übertragen.

Der Stufenwinkel ist dieser, der an einem anderen Schnittpunkt, der durch Parallelverschiebung erzeugt wurde, die gleiche Position einnimmt, wie der Bezugswinkel an seinem Schnittpunkt.

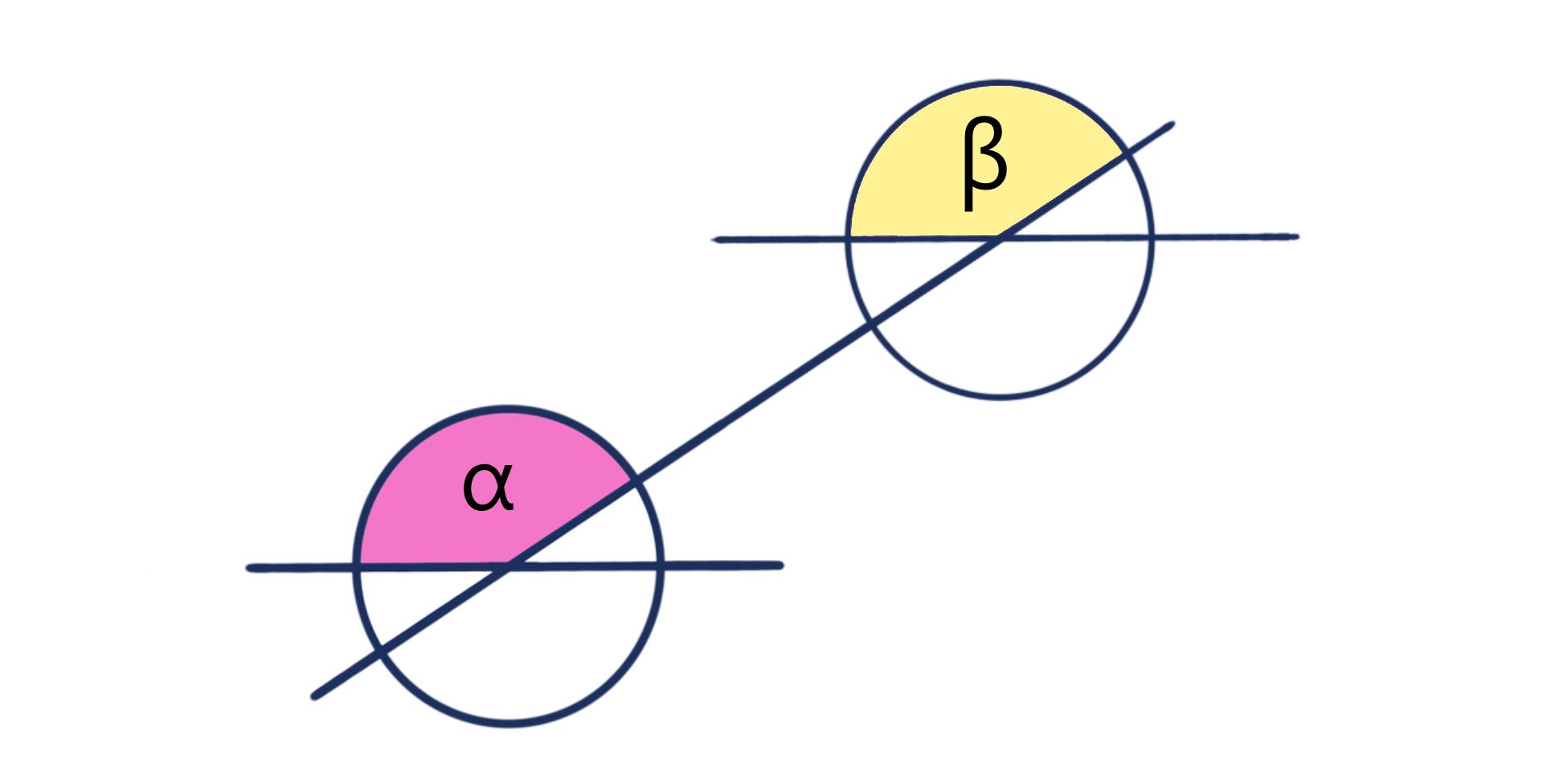
In der unteren Abbildung ist β der Stufenwinkel von α.

Sie haben immer genauso viel Grad wie ihre Bezugswinkel. Wenn man also weiß wie viel Grad α hat, dann weiß man auch wie viel Grad β hat.

Wechselwinkel

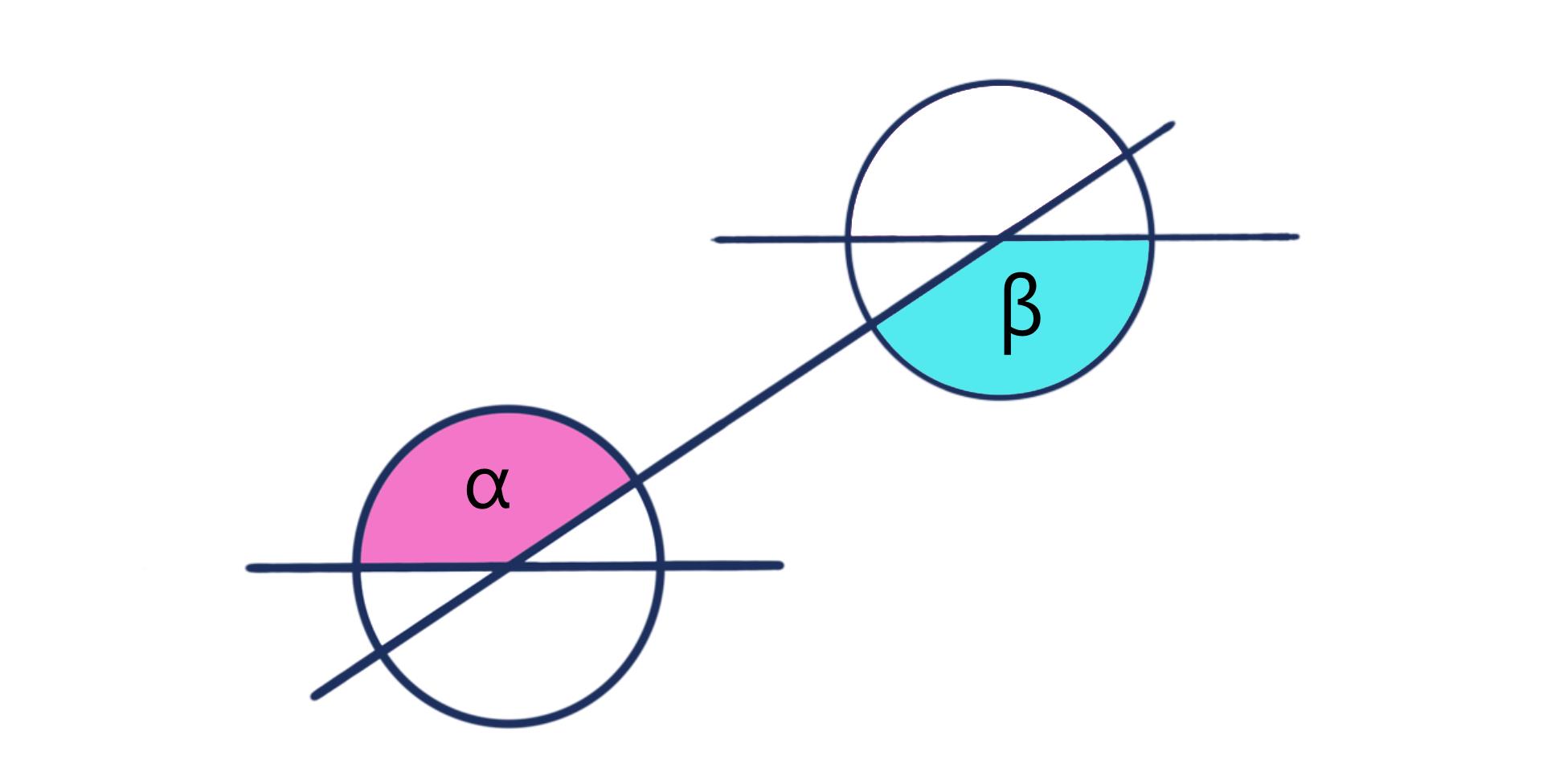
Ein Wechselwinkel ist jener, der an einem anderen Schnittpunkt, der durch Parallelverschiebung erzeugt wurde, die gegenüberliegende Position des Bezugswinkels an seinem Schnittpunkt einnimmt.

In der unteren Abbildung ist β der Wechselwinkel von α.

Sie haben immer genauso viel Grad wie ihre Bezugswinkel. Wenn man also weiß wie viel Grad α hat, dann weiß man auch wie viel Grad β hat.

Zusammenfassung

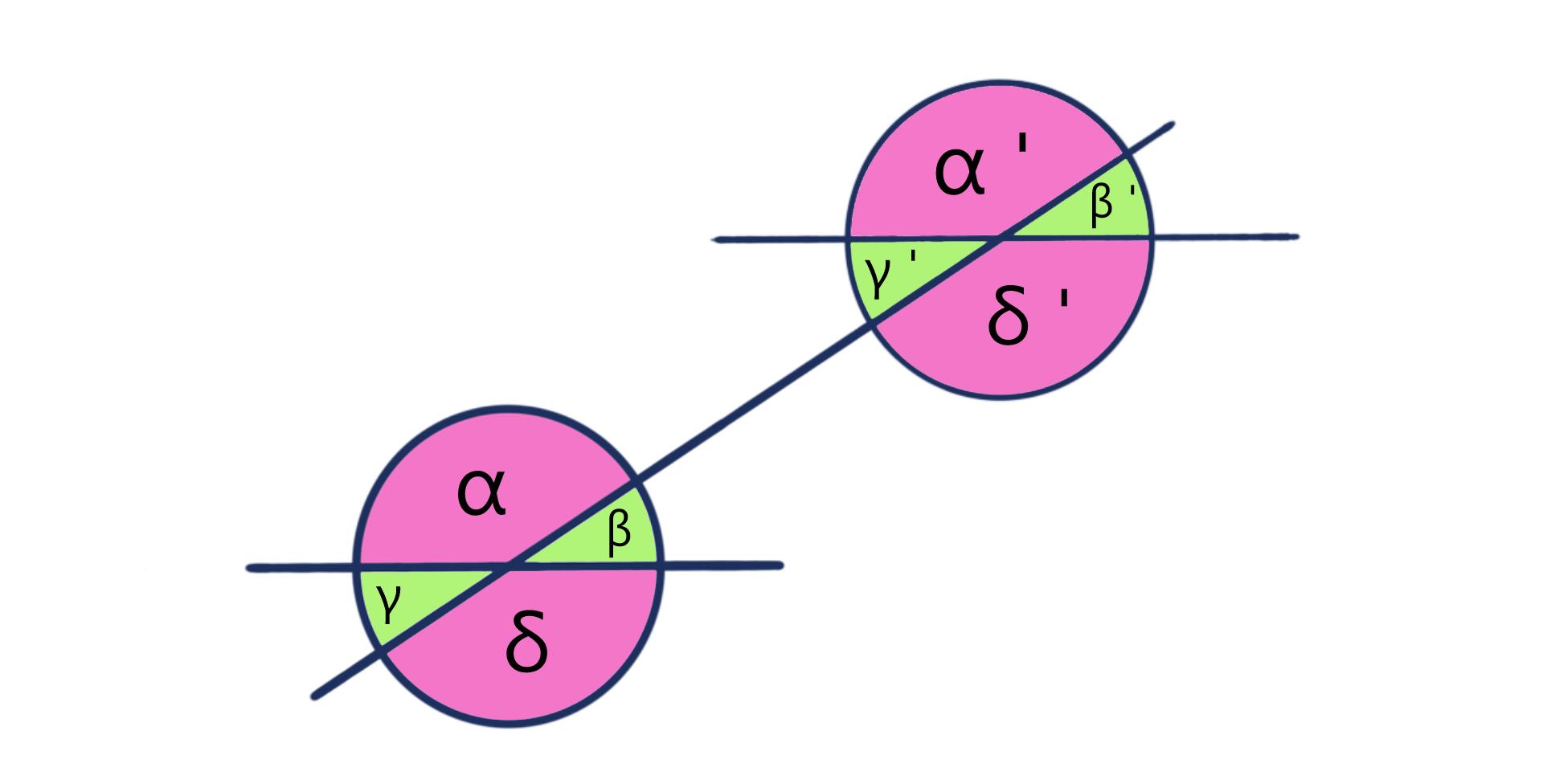
Wenn man all dieses Wissen über die verschiedenen Typen verinnerlicht hat, braucht man nur von einem einzigen Winkel in dem unten abgebildeten Gefüge die Gradzahl kennen und kann sich dann die Größen aller anderen ganz einfach herzuleiten.

Denn in der unteren Abbildung sind alle rosafarbenen Winkel genau gleich groß und alle grünen sind ebenso gleich groß. Das liegt darin begründet, dass sie untereinander für sich die Scheitel-, Stufen- oder Wechselwinkel darstellen. Mithilfe von Nebenwinkeln kann man dann auch die Gradzahl der jeweils andersfarbigen Winkel ermitteln.

Und jetzt noch eine kurze Zusammenfassung für die wichtigsten Fragen:

FAQ