3,75 von 5 Sterne
Loading...
“Lasst uns eine Münze werfen!” Das hast du bestimmt schon mal gehört, wenn du mit deinen Freunden eine Entscheidung treffen willst. In der Mathematik nennt man solch ein Vorgehen Zufallsexperiement, da man nicht zu 100% das Ergebnis vorher sagen kann. Man kann jedoch dieses mittels der Wahrscheinlichkeit berechnen.
Wir zeigen dir in dem Artikel:
- Verständliche Beispiele eines Laplace Experiment
- Ermittlung der absoluten Häufigkeit und deren Bedeutung
- Ermittlung der relativen Häufigkeit und deren Bedeutung
- Erklärung des Erwartungswerts anhand eines Würfelbeispiels
- Wahrscheinlichkeit den Lotto-Jackpot zu gewinnen
Let’s go!
Wahrscheinlichkeit: Definition – Was ist eine Wahrscheinlichkeit?
Eine Wahrscheinlichkeit gibt an, wie hoch die Chance des Eintretens eines Versuchsdurchgangs ist. Diese kann anhand von Formeln berechnet werden. Gängige Beispiele von Wahrscheinlichkeitsexperimenten sind z.B. das Werfen eines Würfels, das Drehen eines Glücksrads oder die Ziehung der Lottozahlen.
Ziehen ohne Zurücklegen
Stell dir vor, du hast eine Urne mit Kugeln vor dir: 6 blaue und 6 rote Kugeln. Du ziehst du jedem Durchgang eine Kugel, ohne sie wieder in die Urne zurückzulegen.
Beim ersten Durchgang beträgt die Wahrscheinlichkeit für eine rote Kugel 6/12 = ½. Denn: Es gibt genauso viele rote wie blaue Kugel in der Urne.
Ziehst du im ersten Durchgang eine rote Kugel und legst diese nicht zurück, ist beim zweiten Durchgang die Wahrscheinlichkeit für eine rote Kugel bereits geringer, denn sie beträgt nur noch 5/11.
Bei einem Wahrscheinlichkeitsbeispiel ohne Zurücklegen verändert sich also die Wahrscheinlichkeit des Eintreffens bei jedem Versuchsdurchgang.
Beim Ziehen ohne Zurücklegen verändert sich die Wahrscheinlichkeit des Eintreffens bei jedem Versuchsdurchgang.
Ziehen mit Zurücklegen
Beim Ziehen mit Zurücklegen bleibt die Wahrscheinlichkeit von Versuch zu Versuch gleich. Ziehen wir z.B. eine Kugel aus einer Urne müssen wir diese wieder zurück legen.
Wir haben 10 Kugeln in einer Urne, 3 blaue 4 rote und 3 grüne Kugeln. Wir ziehen eine grüne Kugel. Da wir diese in dem Experiment zurücklegen haben wir immer noch 10 Kugeln in der Urne.
Die Wahrscheinlichkeiten mit und ohne Zurücklegen kann man auf alle Wahrscheinlichkeitsversuche anwenden.
Beim Ziehen mit Zurücklegen bleibt die Wahrscheinlichkeit von Versuch zu Versuch (d.h. von Ziehungzu Ziehung) gleich.
Laplace-Experiment: Definition – Was ist ein Laplace-Experiment?
Ein Zufallsexperiement wird Laplace-Experiment sobald alle Versuchsergebnisse eine gleiche Wahrscheinlichkeit besitzen.
Bei einem Laplace-Experiment sind alle Ereignisse gleich wahrscheinlich.
Man spricht also für das Eintreten des Ereignisses E:
Beispiele für Laplace-Experimente sind u.a.
- Karten ziehen aus Skatblatt
- Münze werfen
- Kugeln aus Urne ziehen
- Wurf eines Würfels
Keine Laplace-Experimente sind u.a.
- Fußballspiel
- Armdrücken
- Wettrennen
- Tauziehen
- Boxkampf
Absolute und relative Häufigkeit – was ist der Unterschied?
Zwei weitere Begriffe, die ihr sicherlich schon einmal im Zusammenhang mit der Wahrscheinlichkeitsrechnung gehört habt, sind absolute und relative Häufigkeiten. Doch was versteht man darunter und wie lassen sie sich berechnen?
Absolute Häufigkeit berechnen
Die absolute Häufigkeit misst die Häufigkeit eines bestimmten Elementarereignisses. Die absolute Häufigkeit kann grundsätzlich nur natürliche Zahlen annehmen. Dies liegt in der Natur einer Zählung.
Die absolute Häufigkeit lässt sich ganz einfach anhand eines Basketballwurfs auf den Korb darstellen. Wenn ich 10 mal einen Basketball werfe und dieser 4 Mal trifft, dann ist die absolute Wahrscheinlichkeit für das Merkmal 10 die 4.
Die absolute Häufigkeit beschreibt die k Anzahl Treffer in einem Versuch.
Wenn ihr mehr über absolute Häufigkeit erfahren wollt, findet ihr bei uns einen Artikel dazu.
Wenn ich zehnmal einen Basketball auf einen Basketballkorb werfe und davon 4 Würfe in den Korb gehen, beträgt die absolute Häufigkeit für einen Treffer = 4.
Relative Häufigkeit berechnen
Die relative Häufigkeit beschreibt den Anteil der absoluten Häufigkeit eines Merkmals an der Gesamtheit des Experiments. Die Gesamtheit eines Zufallsexperiements beträgt 1=100%. Daher kann die relative Häufigkeit ausschließlich Werte zwischen 0 und 1 annehmen
Die relative Häufigkeit ist der Anteil der absoluten Häufigkeit eines Ereignisses an der Gesamtheitzahl der Ereignisse.
Anhand des Beispiels der absoluten Häufigkeit können wir nun die relative Häufigkeit berechnen.
4/10= 0,4
Schlussfolgernd können wir sagen, dass die relative Wahrscheinlichkeit 4 mal einen Basketball in den Korb zu werfen bei 0,4 liegt also 40%.
Wenn ich zehnmal einen Basketball auf den Basketballkorb werfe und viermal treffe, beträgt die relative Häufigkeit für einen Treffer 4/10 = 0,4 = 40%
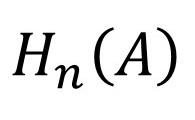
Wenn ihr mehr über relative Häufigkeiten erfahren wollt, findet ihr bei uns einen Artikel dazu.
Wahrscheinlichkeit beim Würfel
Beim Würfelwurf kann man ebenso das Eintreten einer Zahl anhand von Wahrscheinlichkeiten ausrechnen.
Ein Würfel hat 6 verschiedene Möglichkeiten geworfen zu werden, daher ist die Wahrscheinlichkeit des Eintretens einer Zahl (egal ob 1, 2, 3, 4, 5 oder 6) = 1/6. Wenn du also eine 1 würfeln möchtest, hast du die Chance von 1 zu 6 diese tatsächlich zu bekommen. Wollen wir eine 1 und im nächsten Zug eine 4 würfeln, müssen wir beide Wahrscheinlichkeiten multiplizieren.
1/6 * 1/6 ≈ 0,027
Wenn du von einander abhängige Wahrscheinlichkeiten hast, müssen diese immer multipliziert werden.
Erwartungswert beim Würfelwurf
Nehmen wir mal an, wir werfen einen Würfel 20 Mal. und haben folgendes Ergebnis
Gewürfelte Zahlen | 1 | 2 | 3 | 4 | 5 | 6 |
Treffer je Zahl | 4 | 3 | 3 | 3 | 4 | 4 |
Mittels dieses Beispiels können wir nun den Erwartungswert berechnen.
Die Formel sieht wie folgt aus:
E(X) = x1 · P(X = X1 ) + x2 · P(X = x2 ) + … + Xn · P(X = Xn )
Die Formel bedeutet somit nichts anderes als die die Summe aller Wahrscheinlichkeiten, welche mit ihrer Haufigkeit des Eintretens multipliziert wird.
Würfelbeispiel:
E(X) = 4*⅙ + 3*⅙ + 3*⅙ + 3*⅙ + 4*⅙ + 4*⅙ = 3,5
Dieser Wert ist jedoch kein Wert den man direkt in einem Wurf erwarten kann vor allem, weil man keine 3,5 würfeln kann. Jedoch besagt dieser, dass ein Wert in der Nähe des Wertes zu erwarten ist.
Lotto: Wahrscheinlichkeit für einen Lottogewinn
Wer die Nachrichten verfolgt hat oder Zeitung liest, begegnet regelmäßig dem Thema Lottozahlen. Die Ziehung der Lottozahlen ist ebenfalls ein Zufallsexperiment.
Die Wahrscheinlichkeit für 6 aus 49, also den Lotto-Jackpot zu gewinnen, kann man mittels Binomialkoeffizient berechnen.
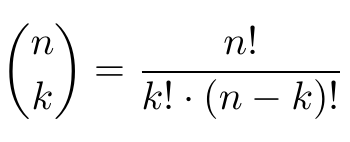
Fakultät bedeutet nichts anderes als das wir jede vorgegebene Zahl für sich bis zur 1 multiplizieren müssen.
Die Wahrscheinlichkeit im Lotto den Jackpot abzuräumen liegt also bei 1 zu 13.983.816, was demzufolge sehr unwahrscheinlich ist.
Wahrscheinlichkeitsrechnung – FAQ
Was ist die Wahrscheinlichkeitsrechnung?
Mithilfe einer Wahrscheinlichkeitsrechnung berechnet man die Wahrscheinlichkeit für das Eintreten eines Ereignisses.
Mehr zur Wahrscheinlichkeitsrechnung
Wahrscheinlichkeit: Formeln - Welche gibt es?
Es gibt viele verschiedene Formeln in der Wahrscheinlichkeitsrechnung.
Wir haben in diesem Artikel:
Laplace-Formel
Formel der relativen Häufigkeit
Formel des Erwartungswertes
E(X) = x1 · P(X = X1 ) + x2 · P(X = x2 ) + … + Xn · P(X = Xn )
Binomialkoeffizient
Wie hoch ist die Wahrscheinlichkeit eine 6 zu würfeln in Prozent?
Wenn wir eine 6 würfeln wollen, müssen wir alle für uns günstigen Versuche durch alle möglichen Versuche teilen (Laplace-Formel). In unserem Fall haben wir nur einen für uns guten Versuch, weil wir eine 6 würfeln wollen.
Im Gegenzug haben wir die Möglichkeit 6 verschiedene Zahlen zu würfeln, dementsprechend haben wir eine Wahrscheinlichkeit von 1/6 eine 6 zu würfeln. Da es sich bei uns um eine Dezimalzahl handelt, müssen wir diese noch umrechnen, um auf den Prozentwert zu kommen.
1/6 ≈ 0,1667
0,1667 · 100 = 16,67%
Die Wahrscheinlichkeit eine 6 zu würfeln liegt bei etwa 16,67%.
Wie hoch ist die Wahrscheinlichkeit 2 mal eine 6 zu würfeln?
Die Wahrscheinlichkeit einmal eine 6 zu Würfeln liegt bei 1/6. Bei einem Würfel handelt es sich um ein Laplace Experiment also teilen wir die Anzahl der günstigen durch die Anzahl der Möglichen Versuche.
Da wir wissen wollen wie hoch die Wahrscheinlichkeit ist, müssen wir die Wahrscheinlichkeiten für die Versuche zweinmal eine 6 zu würfeln multiplizieren.
1/6 · 1/6 ≈ 0,028
0,028 · 100 = 2,80%
Die Wahrscheinlichkeit zweimal eine 6 zu würfeln liegt bei ungefähr 2,8%.
Wie hoch ist die Wahrscheinlichkeit 3 mal Kopf zu werfen?
Die Wahrscheinlichkeit einmal Kopf zu werfen liegt bei einer Münze bei 1/2 also 50%, weil wir nur die Möglichkeit haben Kopf oder Zahl zu werfen. Wenn wir 3 Mal hintereinander Kopf werfen wollen, müssen wir das Eintreten von dreimal Zahl multiplizieren.
Zahl Zahl Zahl → 1/2 · 1/2 · 1/2 = 0,125
0,125 · 100 = 12,5%
Das Eintreten von der Wahrscheinlichkeit dreimal hintereinander Zahl zu werfen liegt bei 12,5%.
Wahrscheinlichkeit berechnen - Konnten wir dir weiterhelfen?
Wir hoffen dir hat der Artikel gefallen. Falls noch Fragen offen sein sollen, du Verbesserungsvorschläge hast oder du vllt. sogar Lob da lassen möchtest. kannst du das sehr gerne tun. Wir freuen uns über deinen Kommentar! 🙂
Hier findest du übrigens alles, was du über die binomischen Formeln wissen musst und hier erfährst du, wer die 7 berühmtesten Mathematiker sind.
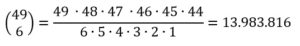
Hallo
ich spiele nun seit über 30 Jahren die gleichen Zahlen bei 6 plus Zusatzzahl (CH)
Wie verbessert sich die Wahrscheinlichkeit bei unterdessen ca. 3000 Ziehungen damit?
Sollte doch besser sein oder gilt da: ziehen mit zurücklegen?
Gruss
Patrick
Deine Chancen verbessern sich nicht. Die Wahrscheinlichkeit ändert sich nicht, da jedes mal 6 aus 49 + Zusatzzahl. Deine Chance liegt bei ~ 1: 140.000.000. Denn das Beispiel im Artikel berücksichtigt die Zusatzzahl nicht.