Vierfeldertafel – einfach erklärt mit Beispielaufgaben und Übungen

4,00 von 5 SterneLoading...

Vierfeldertafel? Was war das noch mal?

Die Vierfeldertafel ist ein Hilfsmittel für die Wahrscheinlichkeitsrechnung. Damit lassen sich die Wahrscheinlichkeiten leicht errechnen und darstellen.

Wie genau das funktioniert, wie du sie anwendest und ausfüllst, das zeigen wir dir jetzt!

Vierfeldertafel einfach erklärt

Die Vierfeldertafel ist ein wichtiges Darstellungsmittel der Stochastik. Mit ihr kannst du die Zusammenhänge zweier Ergebnisse darstellen.

Du kannst in einer Vierfeldertafel sowohl mit Wahrscheinlichkeiten als auch mit absoluten Häufigkeiten arbeiten.

Eine ausgefüllte Vierfeldertafel sieht wie folgt aus:

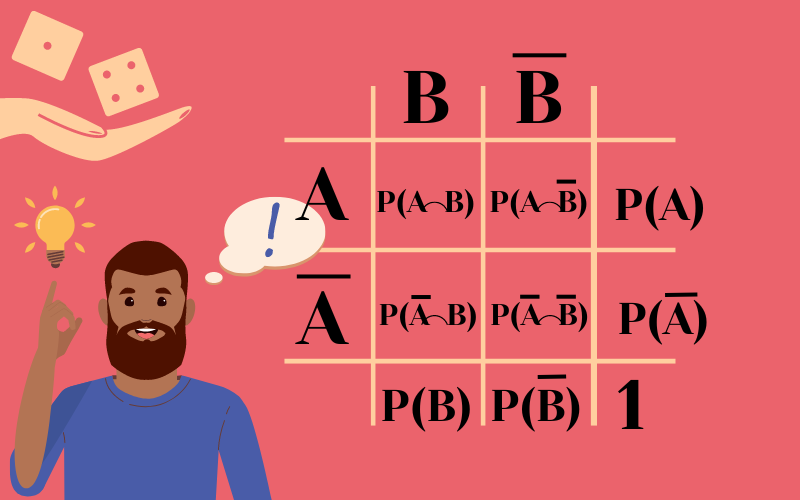
Links außen und oben schreibst du die beiden möglichen Ereignisse. Dabei bedeutet der Strich über diesen, dass das jeweilige Ereignis nicht eintritt.

In den vier mittigen Feldern stehen dann die Schnittmengen der Ereignisse. Also zum Beispiel die Wahrscheinlichkeit dafür, dass A und B beide eintreffen oder A eintrifft, B aber nicht.

Unten und rechts außen stehen dann die Wahrscheinlichkeiten für A und B.

Und zu guter Letzt steht unten rechts in der Ecke dann eine 1.

Aufgaben lösen mit der Vierfeldertafel

Am besten ist die Vierfeldertafel anhand von Beispielen zu verstehen. Gehen wir deshalb von folgender Aufgabe aus:

Vervollständige die Vierfeldertafel. Du kennst folgende Wahrscheinlichkeiten bereits:

P(A) = 0,66
P(B) = 0,4
P(Schnittmenge A, B)= 0,3

Diese Werte übernimmst du nun in deine Tabelle und schreibst unten rechts die 1

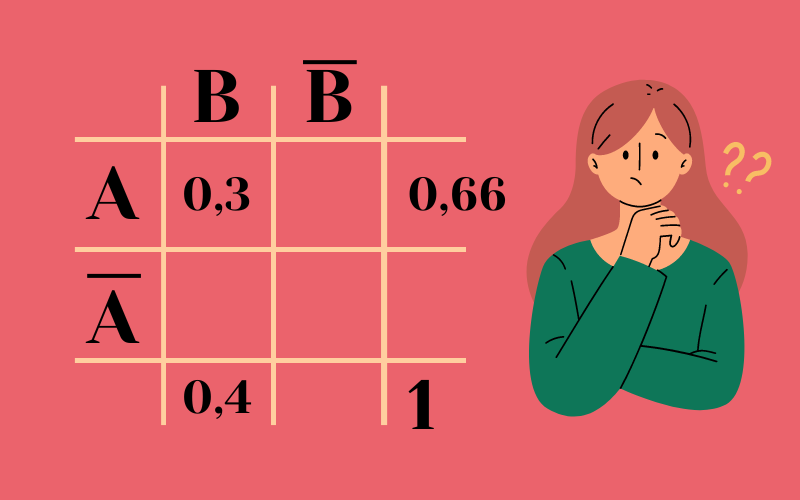
Folgend beginnst du mit den Wahrscheinlichkeiten für P(A) und dem Gegenwert und genau dem gleichen für P(B)

Da die Summe von beiden 1 ergeben muss, kannst du P(A) einfach von 1 subtrahieren und bei P(B) genau das gleiche.

P(nichtA) = 1 – P(A) = 1 – 0,66 = 0,34

P(nichtB) = 1 – P(B) = 1 – 0,4 = 0,6

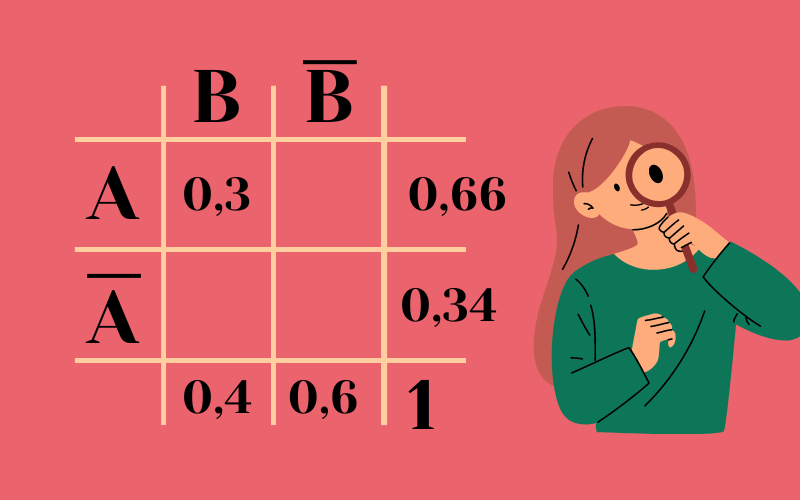
Bei den Schnittmengen kannst du genauso vorgehen, nur dass die Summe zweier Schnittmengen z.B. P(A) ergeben muss.

So rechnest du z.B.

P(Schnittmenge A, nichtB) = P(A) – P(Schnittmenge A, B) = 0,66 – 0,3 = 0,36

Genau so machst du das dann auch noch für die fehlenden Felder.

Ausgefüllt sieht die Vierfeldertafel dann so aus:

Bei einer Aufgabe mit absoluten Häufigkeiten gehst du genauso vor.

Zur Übung versuch doch mal folgende Aufgabe zu lösen. Die ausgefüllte Vierfeldertafel siehst du, wenn du mit der Maus über das Bild gehst.

Wann Vierfeldertafel und wann Baumdiagramm?

Das Baumdiagramm kannst du im Vergleich mit der Vierfeldertafel immer zeichnen. Diese funktioniert nämlich nur, wenn du genau 2 Ausgangs Ereignisse hast.

Außerdem kannst du in einem ausgefüllten Baumdiagramm direkt die bedingte Wahrscheinlichkeit ablesen. Diese findest du nicht in der Vierfeldertafel.

Andersherum kannst du allerdings die Schnittmengen direkt in der Vierfeldertafel finden und im Baumdiagramm wiederum nicht.

Bedingte Wahrscheinlichkeit

Die bedingte Wahrscheinlichkeit steht nicht direkt in der Vierfeldertafel. Du kannst sie aber ausrechnen. Guck doch gerne auf unserer Seite für bedingte Wahrscheinlichkeit vorbei, um zu erfahren, wie das genau funktioniert.