Trigonometrie am rechtwinkligen Dreieck einfach erklärt

Du hast gerade das Thema Trigonometrie in der Schule und fragst dich, wie man die fehlenden Seiten und Winkel eines rechtwinkligen Dreiecks berechnet ?

Damit du eine Aufgabe selbstständig lösen kannst, zeigt dir dieser Artikel, welche Formeln es gibt und wie man sie anwendet.

Lass uns direkt loslegen…

Was ist Trigonometrie?

Trigonometrie besteht aus den zwei griechischen Wörtern trigon und metrie und bedeutet wörtlich “Dreiecksvermessung”. Die grundlegende Aufgabe in der Trigonometrie besteht darin, die Beziehungen zwischen Seiten und Winkeln in einem rechtwinkligen Dreieck zu untersuchen.

Trigonometrie Formeln am rechtwinkligen Dreieck

Damit du aus den gegebenen Größen eines rechtwinkligen Dreiecks die fehlenden Seitenlängen und Winkelgrößen eines Dreiecks berechnen kannst, solltest du die trigonometrische Funktionen “Sinus”, “Cosinus” und “Tangens” kennen.

⇒ und die betrachten wir jetzt einmal näher…

\displaystyle sin\color{green}{(α)} = \frac{\color{blue}{Gegenkathete}}{\color{orange}{Hypotenuse}}\displaystyle = \frac{\color{blue}a}{\color{orange}c}

\displaystyle cos\color{green}{(α)} = \frac{\color{red}{Ankathete}}{\color{orange}{Hypotenuse}}\displaystyle = \frac{\color{red}b}{\color{orange}c}

\displaystyle tan\color{green}{(α)} = \frac{\color{blue}{Gegenkathete}}{\color{red}{Ankathete}}\displaystyle = \frac{\color{blue}a}{\color{red}b}

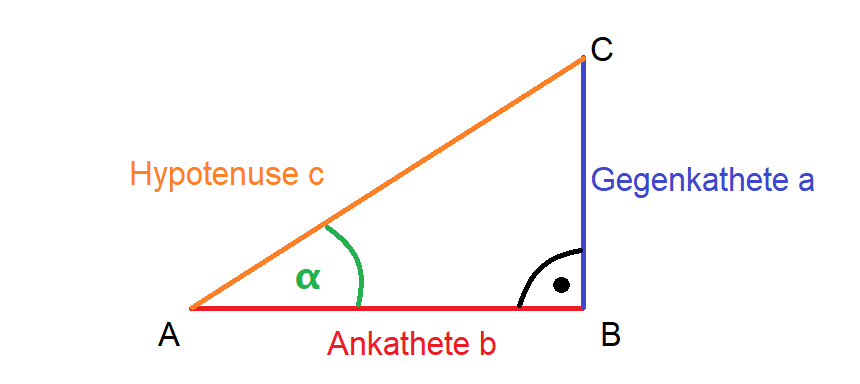
Es ist gegeben die Gegenkathete a, die unserem Winkel α gegenüberliegt. Die Ankathete b ist die Kathete, die direkt an dem Winkel α anliegt. Zu beachten ist, dass die längste Seite im rechtwinkligen Dreieck die Hypotenuse c ist. Sie befindet sich gegenüber dem rechten Winkel.

Seiten eines rechtwinkligen Dreiecks berechnen – Schritt für Schritt

Mithilfe der drei Trigonometrie Formeln können wir nun die fehlenden Seiten und Winkeln eines rechtwinkligen Dreiecks berechnen. Dazu gucken wir uns die folgende Aufgabe an.

Trigonometrie Seiten berechnen – Beispiel: 

Angenommen das folgende rechtwinklige Dreieck beinhaltet folgende Werte:

Gegeben:   c = 5 cm (Hypotenuse)     α = 30° (Winkelgröße)          Gesucht: a (Gegenkathete)

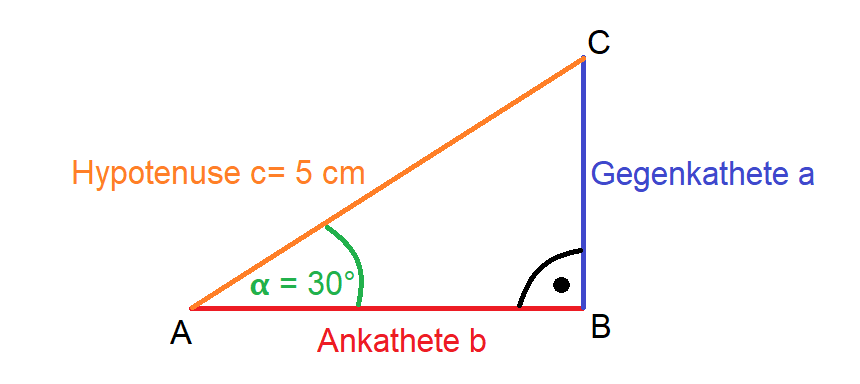
In unserer Skizze sehen wir, dass wir die Sinusfunktion verwenden müssen, um unsere fehlende Komponente (Gegenkathete a) zu berechnen.

\displaystyle sin\color{green}{(α)} = \frac{\color{blue}{Gegenkathete}}{\color{orange}{Hypotenuse}}\displaystyle = \frac{\color{blue}a}{\color{orange}c}

1. Zunächst müssen beide Werte in die Formel eingesetzt werden.

\displaystyle sin\color{green}{(30°)} = \frac{\color{blue}{a}}{\color{orange}{5 cm}}

2. Die Formel stellst du nach der Gegenkathete um und multiplizierst auf beiden Seiten der Gleichung mit 5 cm.

\displaystyle sin\color{green}{(30°)} = \frac{\color{blue}{a}}{\color{orange}{5 cm}} | ⋅ 5 cm

3. Damit erhältst du das Ergebnis der Gegenkathete a. Die Seitenlänge beträgt 2,5 cm.

sin (30°) ⋅ 5 cm = a

2,5 cm = a

Winkel eines rechtwinkligen Dreiecks berechnen – Schritt für Schritt

Nun bist du bereits in der Lage, alle möglichen Seitenlängen zu berechnen. Wie du den Winkel berechnen kannst, erfährst du im nächsten Beispiel.

Trigonometrie Winkel berechnen – Beispiel: 

Für das folgende rechtwinklige Dreieck sind folgende Werte gegeben:

Gegeben:   b = 4 cm (Ankathete)     c = 8cm (Hypotenuse)          Gesucht: α (Winkelgröße)

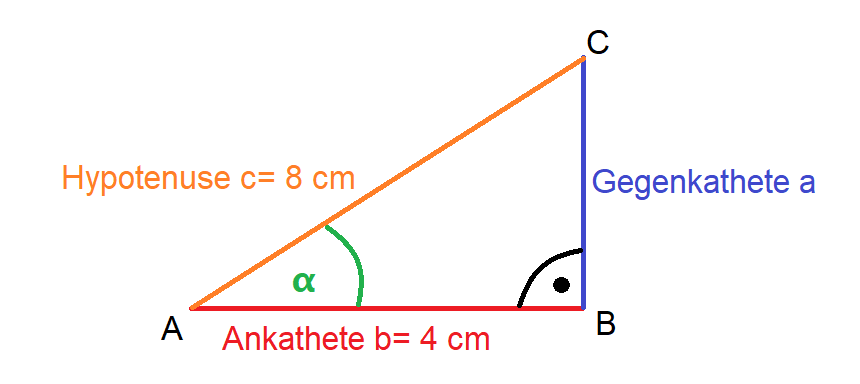
Die Skizze gibt uns die Information, dass wir die Kosinusfunktion verwenden müssen, um die Winkelgröße zu bekommen.

\displaystyle cos\color{green}{(α)} = \frac{\color{red}{Ankathete}}{\color{orange}{Hypotenuse}}\displaystyle = \frac{\color{red}b}{\color{orange}c}

1. Beide Werte der Seitenlängen in die Trigonometrie Formel einsetzen.

\displaystyle cos\color{green}{(α)} = \frac{\color{red}{4 cm}}{\color{orange}{8 cm}}

2. Auf der rechten Seite dividierst du die zwei Zahlen. Du erhältst cos (α)= 0,5.

cos (α) = 0,5

3. Das Ergebnis setzt du dann in die Umkehrfunktion von Cosinus, also in \displaystyle cos^{-1}. Um nun die Winkelgröße des rechtwinkligen Dreiecks zu bekommen, kannst du die \displaystyle cos^{-1} – Taste auf deinem Taschenrechner verwenden.

α = \displaystyle cos^{-1}(0,5)

4. Du erhältst die Winkelgröße des rechtwinkligen Dreiecks. Der Winkel beträgt 60°.

α = 60°

Trigonometrie Tabelle

Hier siehst du eine Wertetabelle, die du dir merken kannst. Zu einigen Winkeln der trigonometrischen Funktionen gibt es besondere Funktionswerte, die sich als Wurzelausdrücke darstellen.

Beispiel: 

Folgende Werte  sind für ein rechtwinkliges Dreieck gegeben.

Gegeben:   c = 6 cm (Hypotenuse)     α = 30 ° (Winkelgröße)           Gesucht: b (Ankathete)

1. Kosinusfunktion anwenden

\displaystyle cos\color{green}{(α)} = \frac{\color{red}{Ankathete}}{\color{orange}{Hypotenuse}}\displaystyle = \frac{\color{red}b}{\color{orange}c}

2. Du guckst in die Tabelle und nimmst den Cosinus- Wert für 30°. In die Formel setzt du also √3/2 ein.

\displaystyle\color{green}{√3/2} = \frac{\color{red}{b}}{\color{orange}{6 cm}}

3. Die Formel stellst du nach der Ankathete um und multiplizierst auf beiden Seiten der Gleichung mit 6 cm. Du erhältst ein Ergebnis der Seitenlänge von 3√3 cm.

\displaystyle\color{green}{√3/2} = \frac{\color{red}{b}}{\color{orange}{6 cm}} | ⋅ 6 cm

√3/2 ⋅ 6 cm = b

3√3 cm = b

Trigonometrie Aufgaben

Und nun bist du an der Reihe! Teste dein Wissen anhand der Übungsaufgaben und schaue, ob du die Formeln richtig anwendest.

FAQ