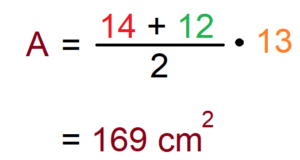4,80 von 5 Sterne
Loading...
Du bist dir unsicher, was ein Trapez ist? Du möchtest wissen, wie man es berechnet?
Dann bist du bei uns genau richtig. Hier werden dir die wichtigsten Eigenschaften und Formeln mit Beispielen kurz erklärt.
Teste am Ende dein Wissen mit unseren Übungen!
Ein Trapez ist immer ein Viereck, aber ein Viereck ist nicht immer ein Trapez!
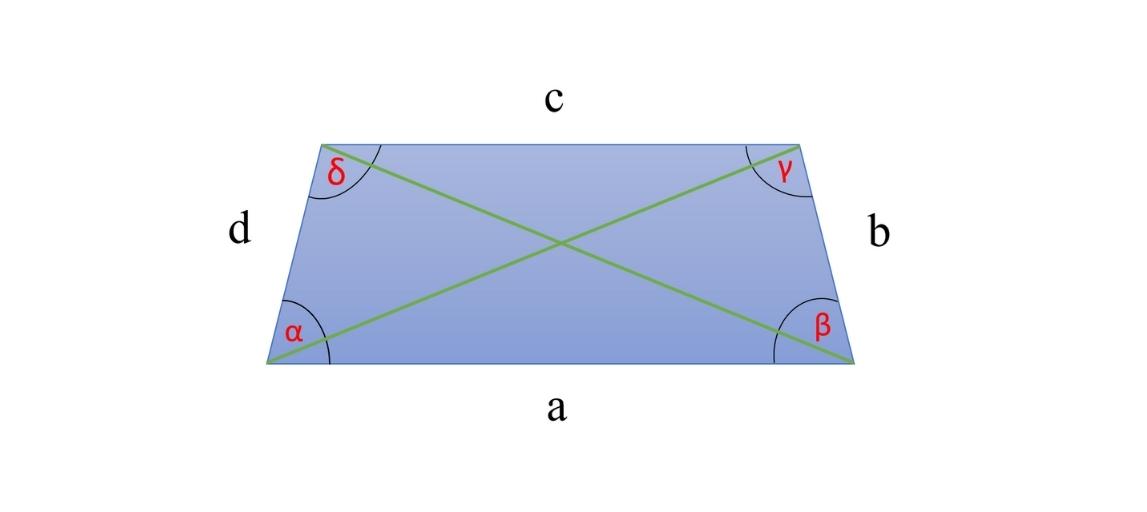
Trapez Eigenschaften
Ein Trapez hat…
- zwei Diagonalen
- vier Ecken
- vier Winkel
- vier Seiten
Die beiden anderen Seiten, die nicht die Grundseiten sind, werden Schenkel genannt.
Die Innenwinkel, die an einem Schenkel anliegen, ergeben zusammen immer 180°!
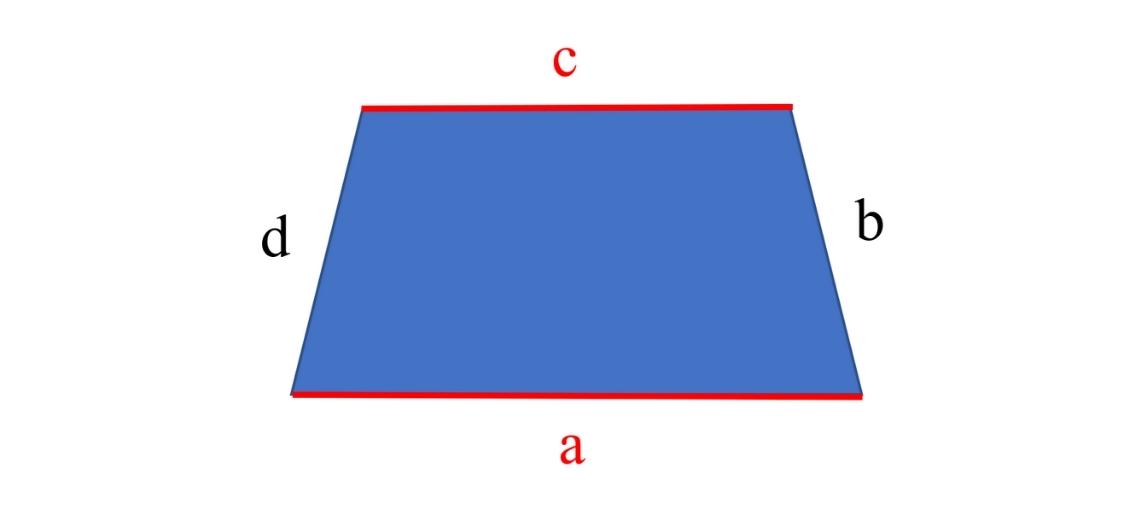
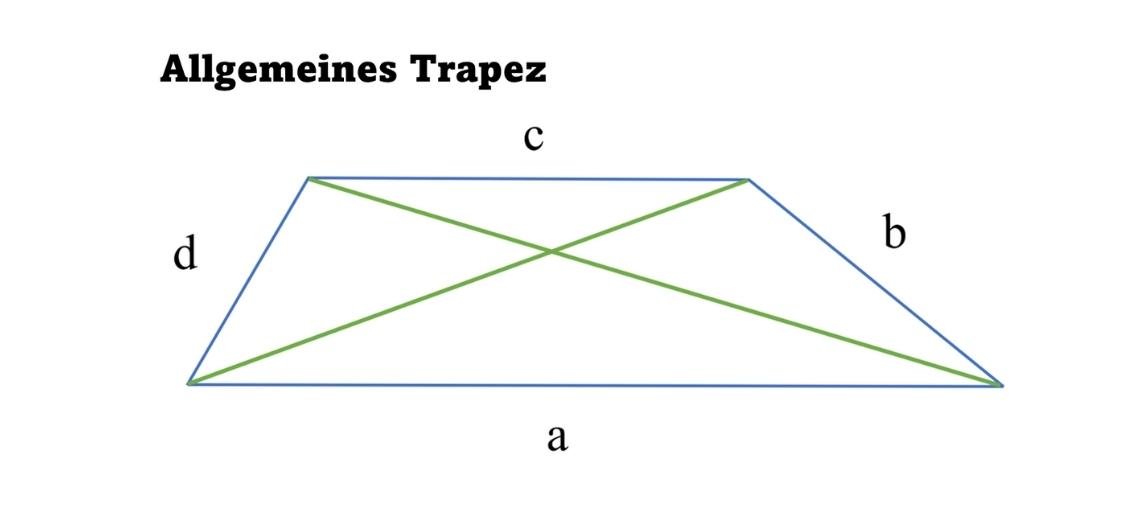
Wie sieht ein Trapez aus?
Es besitzt eine Höhe h und eine Mittellinie m. Die Höhe ist der Abstand der Grundseiten. Die Mittellinie ist die Verbindungsstrecke der Mitten der beiden Schenkel.
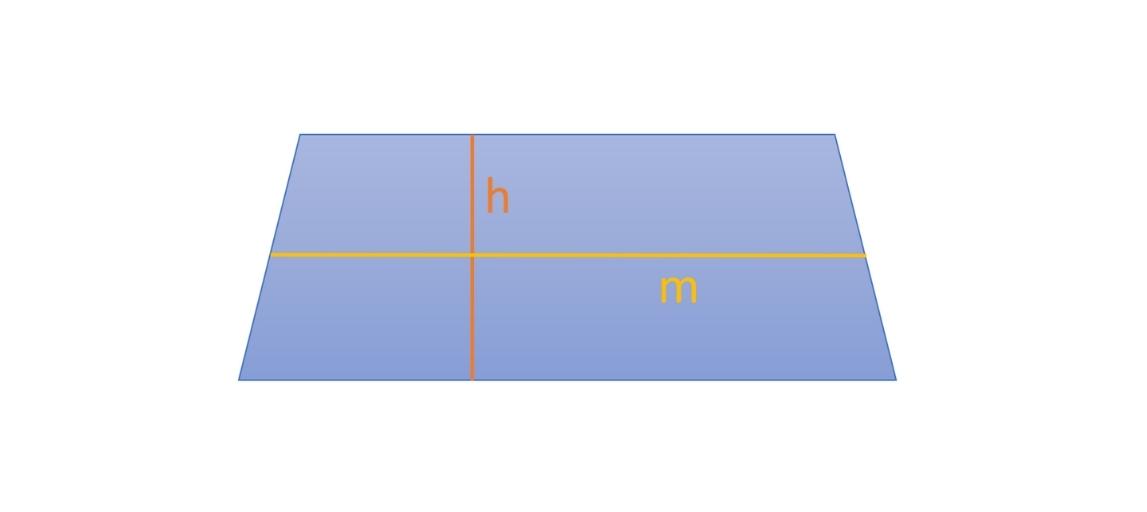
Die Mittellinie verläuft immer parallel zu den Grundseiten. Sie ist halb so lang wie die Summe der beiden Grundseiten:
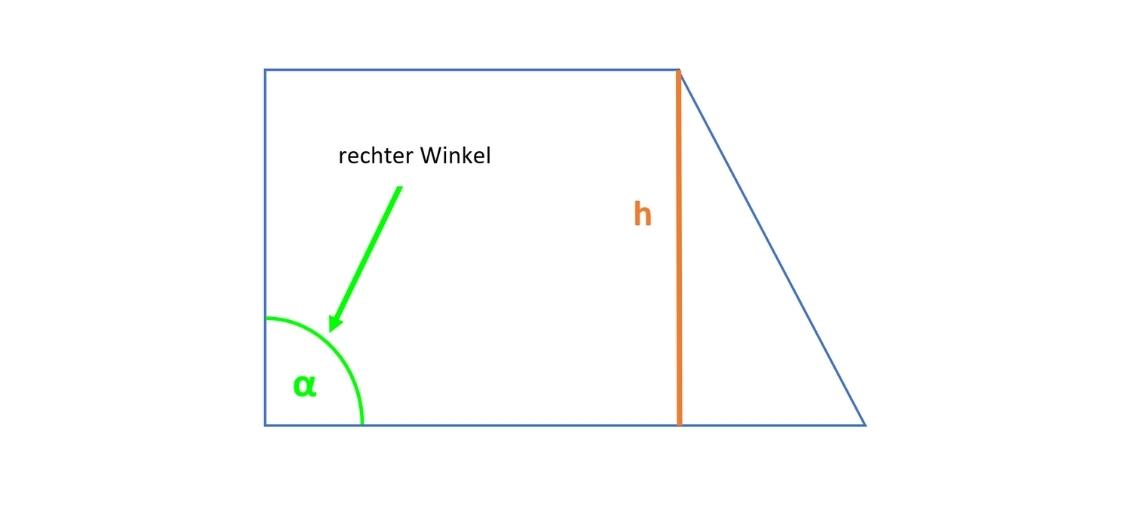
Rechtwinkliges Trapez
Ein solches Viereck hat mindestens einen rechten Innenwinkel (also ein Winkel von 90°).
Die Höhe h ist dabei der Schenkel, der sich auf den parallelen Seiten senkrecht befindet.
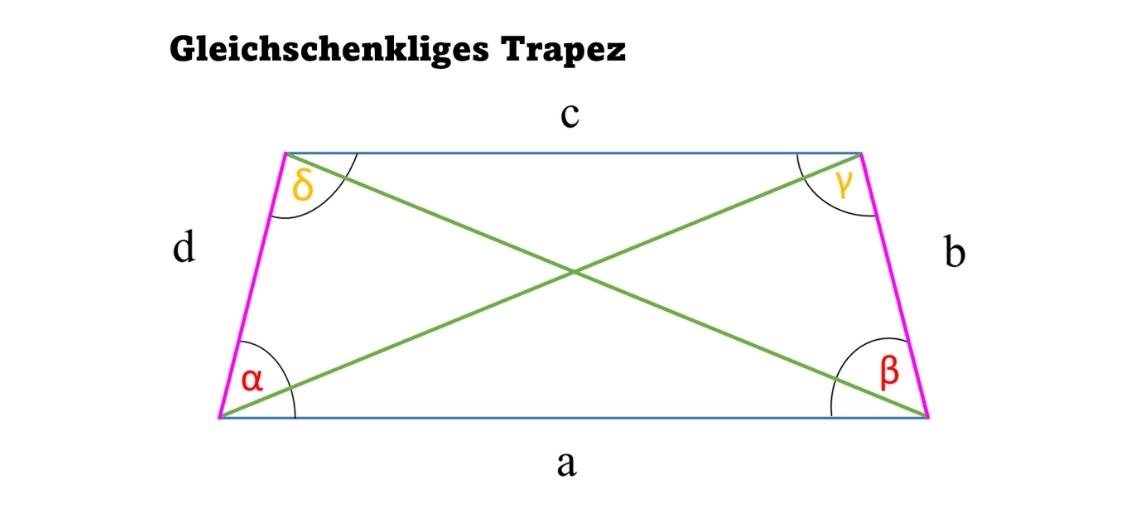
Gleichschenkliges Trapez
Wenn die Schenkel gleich lang sind, wird so eine Art von Viereck gleichschenklig genannt. Es ist achsensymmetrisch, weswegen es auch symmetrisches Trapez genannt wird.
Ein gleichschenkliges/symmetrisches Trapez hat:
- zwei gleich lange Schenkel
- zwei gleich große Innenwinkel an der parallelen Seite
- Innenwinkel, die sich an den Schenkeln zu 180° ergänzen
- gleich lange Diagonalen
Die Symmetrieachse ist die Mittelsenkrechte der zueinander parallelen Seiten.
Trapez berechnen
Für so ein Viereck kannst du den Umfang und den Flächeninhalt berechnen.
Wir zeigen dir, wie schnell und einfach das geht!
Umfang Trapez
Den Umfang U berechnest du, indem die die vier Längen der Seiten addierst:
Der Umfang von einem gleichschenkligen Trapez wird so berechnet:
U = a + 2b + c
Beispiel: Umfang berechnen
Wie ist der Umfang mit den gegebenen Maßen a = 12 cm, b = 6 cm, c = 14 cm und d = 6 cm?
→ Einsetzen der gegebenen Werte in die Umfang Formel:
12 + 6 + 14 + 6 = 38 cm.
→ Der Umfang beträgt 38 cm.
Flächeninhalt Trapez
Zur Flächenberechnung Trapez musst du die Trapez Flächeninhalt Formel anwenden.
Guck dir in diesem Zusammenhang unseren Artikel zum Thema Flächeninhalt berechnen an!
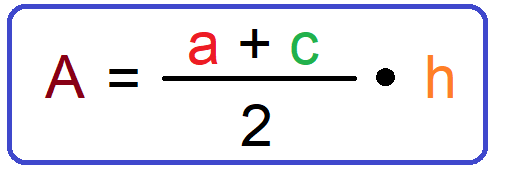
Beispiel: Fläche berechnen
Berechne die Fläche mit den Maßen a = 14 cm, c = 12 cm, und h = 13 cm.
→ Einsetzen der gegebenen Werte in die Flächeninhalt Formel:
→ Der Flächeninhalt ist also 169 cm².
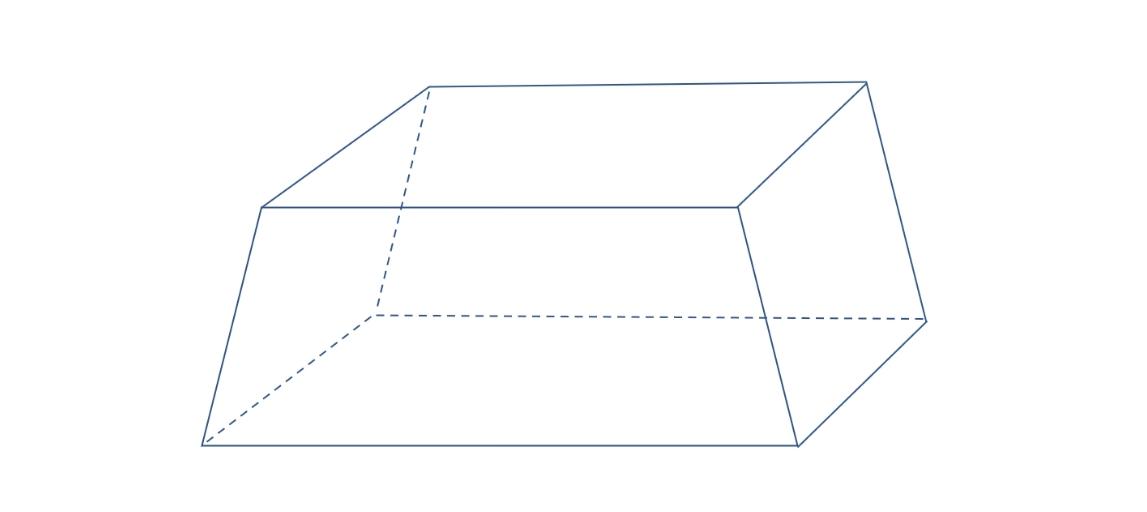
Trapezprisma
Ein Trapezprisma ist ein Prisma mit trapezförmiger Grundfläche.
Es hat 12 gleich lange Kanten und setzt sich aus zwei Trapezen (Grund- und Deckfläche) und vier Rechtecken zusammen.
Die Grund- und Deckfläche sind kongruent, also deckungsgleich, und parallel zueinander.
Trapez Volumen
Du kannst für ein Trapez kein Volumen berechnen, weil es zweidimensional ist. Das Volumen ist der räumliche Inhalt eines Körpers und wird für dreidimensionale Körper errechnet.
Du kannst allerdings das Volumen für Trapezprismen berechnen!
Wir zeigen dir, wie simpel das geht!
Die Formel für das Trapezprisma Volumen lautet:
Was eine Grundfläche und Höhe bei einem Trapez ist, hast du weiter oben schon erfahren. Nun berechnest du einfach die Grundfläche, also den Flächeninhalt, und die Höhe und multiplizierst diese beiden miteinander.
Schon hast du das Volumen des Prismas errechnet!
Trapez und Parallelogramm
Parallelogramme sind spezielle Trapeze. Sie haben auch zwei parallele Seiten. Während bei einem Parallelogramm die gegenüberliegenden Seiten parallel und gleich lang sind, sind die Seiten bei einem Trapez zwar auch parallel, aber nicht zwingend gleich lang.
Merke: Ein Parallelogramm ist also immer ein Trapez, aber ein Trapez ist nicht immer ein Parallelogramm.
Schau dir hierzu unseren Artikel über das Parallelogramm an.
Trapez Formeln
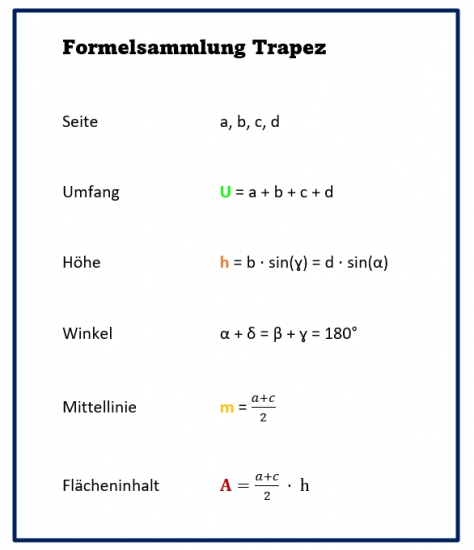
Als kleine Hilfe haben wir dir hier eine Trapez Formelsammlung zum Herunterladen bereitgestellt!
Übungen
Jetzt bist du dran! Hier kannst du dein Wissen auf die Probe stellen und die Übungsaufgaben bearbeiten.
Klick einfach auf das +, um die Lösung zu sehen!
Was ist ein Trapez?
Ein Trapez ist ein Viereck mit zwei parallel verlaufenden Grundseiten. Die längere Grundseite wird meistens Basis genannt. Die anderen beiden Seiten heißen Schenkel. Ein solches Viereck hat außerdem immer vier Innenwinkel, die zusammen gerechnet 360° ergeben.
Berechne den Umfang von einem Trapez mit den Seiten a = 10 cm, b = 4 cm, c = 9 cm und d = 5 cm.
U = 10 + 4 + 9 + 5
= 28 cm
→ Der Umfang beträgt 28 cm.
Was ist ein Trapezprisma?
Ein Trapezprisma ist ein Prisma mit trapezförmiger Grundfläche. Es hat 12 gleich lange Kanten, zwei Trapeze (Grund- und Deckfläche) und vier Rechtecke.
Die Grund- und Deckfläche sind kongruent und parallel zueinander.
Berechne den Flächeninhalt Trapez mit den Maßen a = 6 cm, c = 4 cm und h = 5 cm.
A = (6 + 4) : 2 ⋅ 5
= 25
→ Der Flächeninhalt beträgt 25 cm².
Erkläre, was ein gleichschenkliges Trapez ist.
Ein gleichschenkliges Trapez hat zwei gleich lange Schenkel, zwei gleich große Innenwinkel an der parallelen Seite und Innenwinkel, die sich an den Schenkeln zu 180° ergänzen. Man kann es auch symmetrisches Trapez nennen, weil es achsensymmetrisch ist.
Wir hoffen du konntest dich gut an unseren Erklärungen entlanghangeln ?
Wie hat dir der Artikel gefallen?
Nimm dir kurz Zeit und lass uns gerne einen Kommentar in den Bewertungen da!
4,80 von 5 SterneLoading...
