4,22 von 5 Sterne
Loading...
Du fragst dich, was Strahlensätze in der Geometrie sind und wofür du sie brauchst?
Wir zeigen dir in diesem Artikel…
- … wann du einen Strahlensatz anwenden musst
- … welche Strahlensätze es gibt
- …wie du ganz einfach in 5 Schritten Strahlensätze berechnen kannst
Lass uns zuerst klären, was Strahlensätze sind.
Wofür brauche ich Strahlensätze?
Mit dem ersten und zweiten Strahlensatz kannst du eine unbekannte Strecke ausrechnen.
Strahlensätze werden nicht nur in der Geometrie verwendet, sondern beispielsweise auch um die Entfernung zwischen zwei Gebäuden oder die Höhe eines Turmes zu berechnen.
Damit du mit Strahlensätzen rechnen kannst, müssen zuerst folgende Voraussetzungen beachtet werden:
Voraussetzungen für die Anwendung:
- Es müssen mindestens 2 Strahlen gegeben sein, die einen gemeinsamen Punkt besitzen. Diesen Punkt bezeichnet man als Scheitel (S).
- Diese 2 Strahlen müssen von 2 Geraden geschnitten werden, die parallel zueinander verlaufen. Dies wird immer mit g||h gekennzeichnet. Das bedeutet, g ist parallel zu h.
- Dabei dürfen die parallelen Geraden die 2 Strahlen nicht am Scheitel treffen
Der 1. Strahlensatz
Durch den 1. Strahlensatz wird das Verhältnis zwischen den kurzen und langen Streckenabschnitten auf den zwei Strahlen beschrieben.
Formel zum 1. Strahlensatz
Durch die Formel wird ausgedrückt, dass sich die zwei Abschnitte auf dem einen Strahl wie die entsprechenden gleich liegenden Abschnitte auf dem zweiten Strahl verhalten.
Formel zum 1. Strahlensatz:
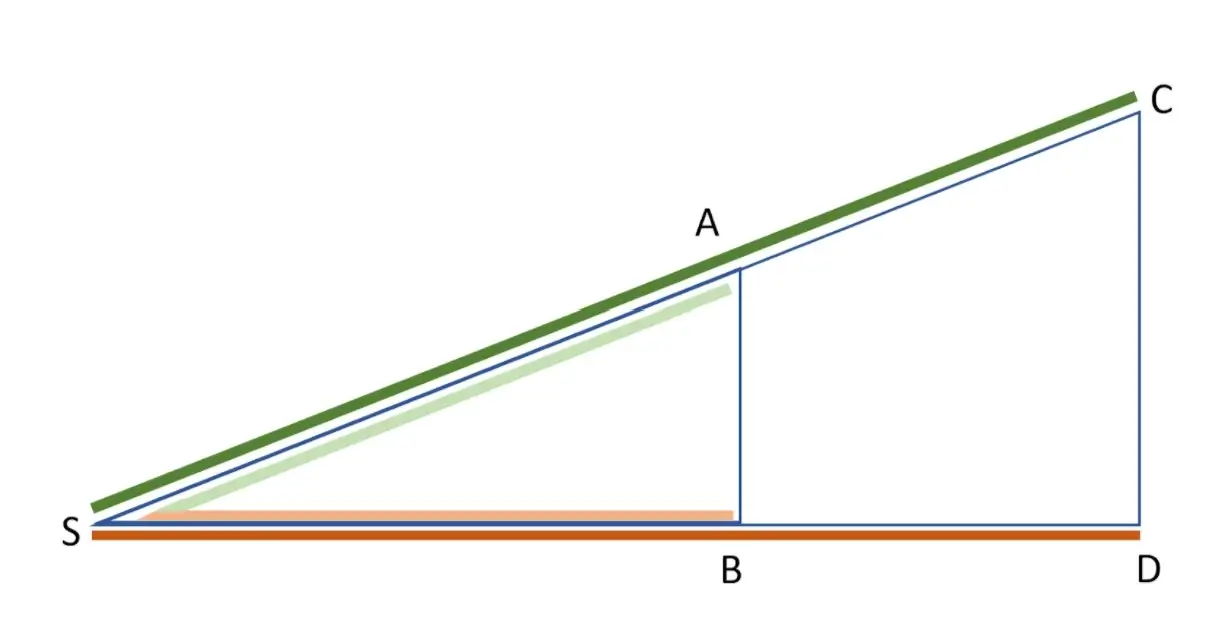
Ein Strich über den Buchstaben bedeutet immer die Strecke zwischen zwei Punkten. Also bedeutet 
die Strecke zwischen dem Scheitel (S) und dem Punkt A.
Damit du auch weißt, wie die Formel angewendet wird, haben wir hier eine Beispielaufgabe für dich vorgerechnet.
So gehst du vor, wenn du den 1. Strahlensatz anwendest, um die Länge einer Strecke zu berechnen.
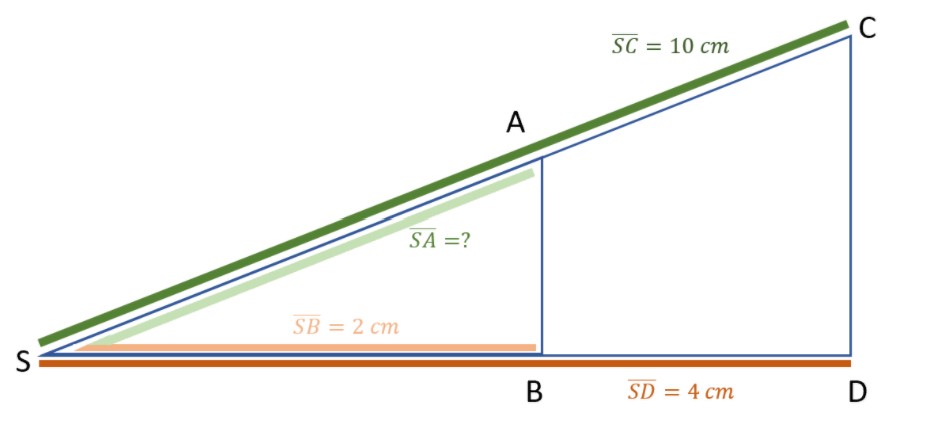
Du hast die folgenden Seitenlängen eines Dreiecks gegeben: 
= 10cm, 
= 2cm,
= 4cm. Gesucht ist die Länge der Seite .
- Schritt: Skizze anfertigen
2. Die richtige Formel aussuchen
3. Nach der gesuchten Größe umstellen
4. Gegebene Werte einsetzen
5. Ergebnis berechnen
Die Länge der Strecke beträgt 5cm.
Der 2. Strahlensatz
Der 2. Strahlensatz besagt, dass das Verhältnis der Parallelen gleich dem Verhältnis der Strecken auf einem der Strahlen ist.
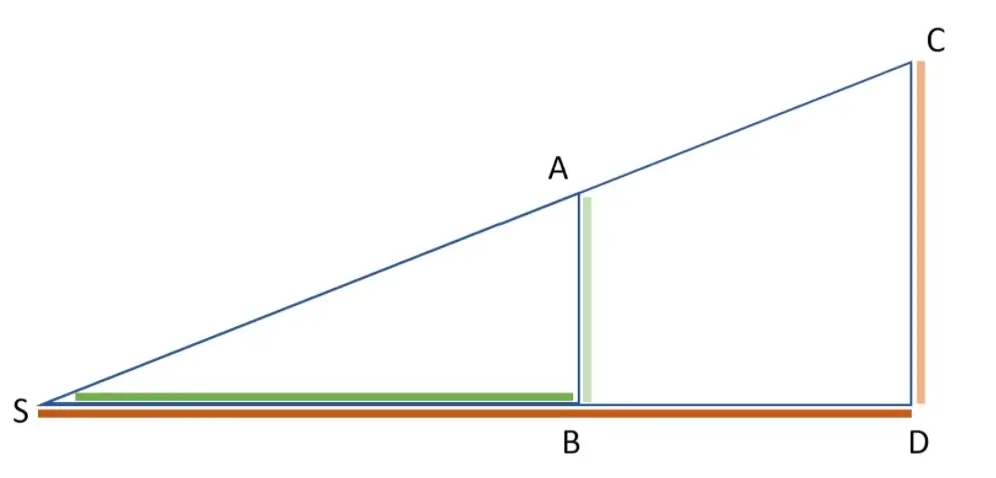
Wie bei der Formel des 1. Strahlensatzes, kannst du Zähler und Nenner in den Brüchen vertauschen.
Formel zum 2. Strahlensatz:
Auch hier haben wir eine Beispielaufgabe für dich. So wendest du die Formel zum 2. Strahlensatz an.
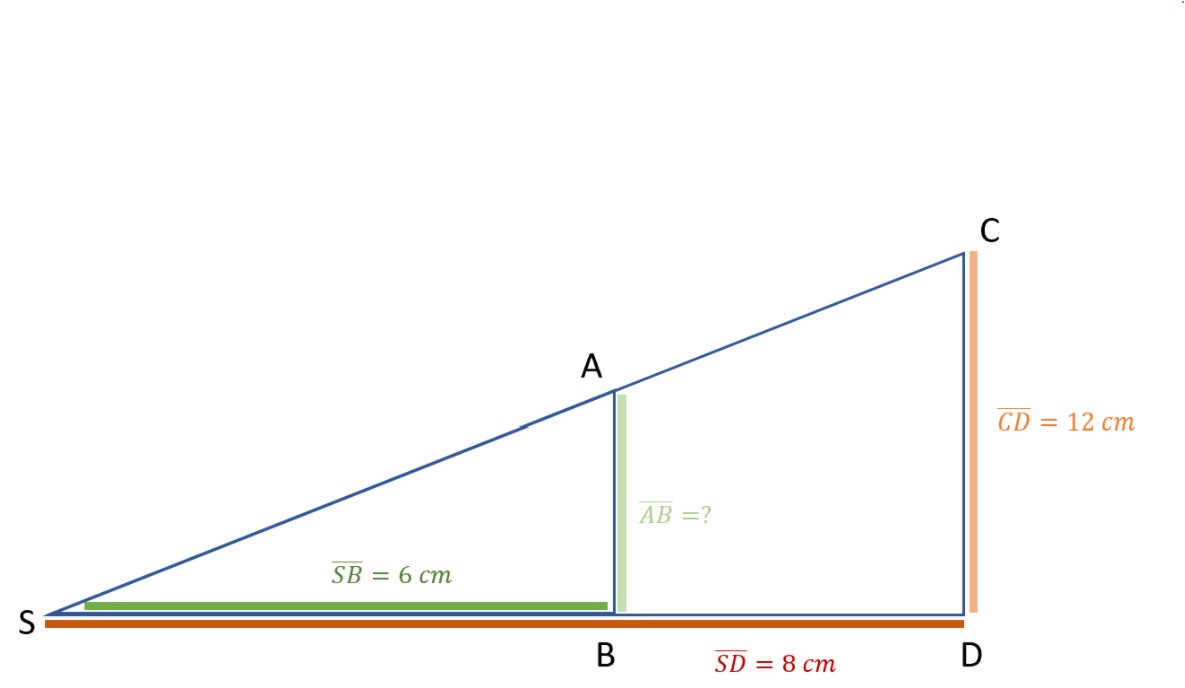
Du hast folgende Seitenlängen im Dreieck gegeben: = 6cm, = 8cm,
= 12cm. Gesucht ist die Länge der Seite 
.
- Skizze anfertigen
2. Den richtigen Strahlensatz aussuchen
3. Nach der gesuchten Größe umstellen
4. Gegebene Werte einsetzen
5. Ergebnis berechnen
Die Länge der Strecke beträgt 9 cm.
Eine Anwendungsaufgabe
Jetzt bist du an der Reihe mit dem Rechnen. Dafür haben wir eine Aufgabe für dich, die so oder so ähnlich auch in deiner nächsten Matheklausur vorkommen kann.
Du stehst an dem Punkt S. 2 km von dir entfernt befindet sich ein 100 Meter hohes Haus. 15 km von dem Haus entfernt befindet sich der Leuchtturm. Berechne die Höhe des Leuchtturms.
Hier siehst du alle Angaben in einem Bild zusammengefasst:
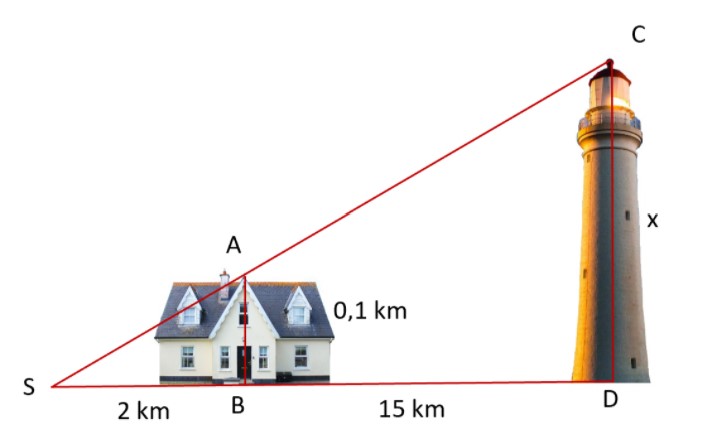
1. Zuerst fertigen wir eine Skizze an:
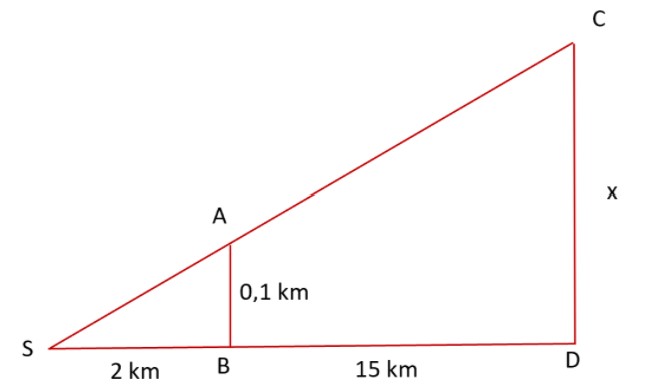
2. Den richtigen Strahlensatz aussuchen
Gesucht ist die Höhe des Leuchtturms, also die Länge der Seite . Dies bedeutet wir nehmen den 2. Strahlensatz.
3. Nach der gesuchten Größe umstellen
Damit die Umstellung nach leichter ist, tauschen wir zuerst bei beiden Brüchen die Nenner und Zähler.
Jetzt können wir die Gleichung leichter nach der gesuchten Größe umformen.
4. Gegebene Werte einsetzen
Zunächst müssen wir die Strecke berechnen. Wir wissen, dass das Haus 2 km von uns entfernt ist und 15 km hinter dem Haus befindet sich der Leuchtturm. Das bedeutet, dass der Leuchtturm 2 km + 15 km = 17 km weit von uns entfernt ist. Also ist die Länge der Strecke 17 km.
5. Ergebnis berechnen
Die Höhe des Leuchtturms beträgt 0,85 km, also 850 Meter.
Wenn du weitere Übungsaufgaben suchst, dann schau hier oder vorbei. Auch können wir dir diese Webseite sehr empfehlen.
FAQ
Wie lautet die Formel für den 1. Strahlensatz?
Die Formel für den 1. Strahlensatz lautet
Wie lautet die Formel für den 2. Strahlensatz?
Die Formel für den 2. Strahlensatz lautet
Wofür kann ich die Strahlensätze verwenden?
Die Strahlensätze kannst du verwenden, um die Länge einer Strecke zu berechnen.
Wann kann ich Strahlensätze anwenden?
Die Voraussetzung für die Anwendung der Strahlensätze ist, dass es mindestens zwei Strahle mit einem gemeinsamen Punkt geben muss, die von zwei parallelen Geraden geschnitten werden.
Hat dir der Inhalt geholfen? Lass uns gerne einen kurzen Kommentar da, wir würden uns sehr freuen!
Ansonsten findest Du weitere hilfreiche Erklärungen zu verschiedenen Themengebieten auf der Homepage des Nachhilfe-Teams.
Hast du schon von unserer Online Nachhilfe gehört? Zusätzlich zu unserer Vor-Ort-Mathe Nachhilfe betreuen wir dich auch online ganz flexibel! Probiere es direkt aus 😉
Bevor du gehst...
…würden wir uns riesig über deine Bewertung freuen! Damit tust du uns einen großen Gefallen. Dankeschön! 🙂
4,22 von 5 SterneLoading...
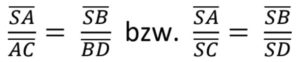
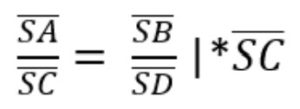
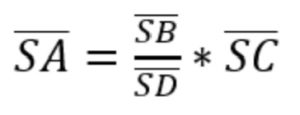
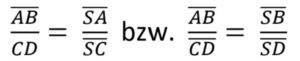
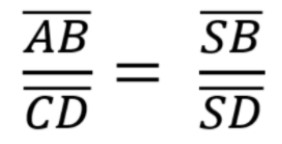
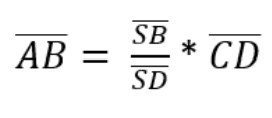
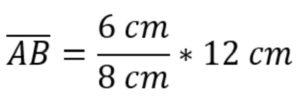
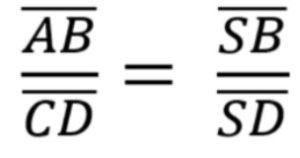
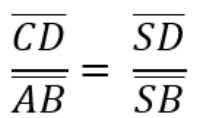
Vielen Dank für die super tolle und sehr klar definierte Ausführung.
Das hat mir sehr, sehr gut geholfen. Toll nachvollziehbar!
Genial!!!
Wirklich gut erklärt
Ich sollte meiner -nichte (9. Klasse) Strahlensätze erklären, bin allerdings selbst schon 35 Jahre aus der Schule raus. Zum Wiederanlesen ist die Erklärung perfekt!
Supertoll optisch aufbereitet und sehr schön nachvollziehbar erklärt!! Vielen Dank für eure Mühe!!!
Vielen Dank für die tolle Erklärung. Noch besser fände ich es wenn die Ergebnisse auch plausibel wären. Ein Haus mit 100m Höhe und ein Leuchtturm mit 850 m Höhe trifft man eher selten an. :-).
Vielen Dank, für dein Feedback Katja. Wir freuen uns, dass der Beitrag dir helfen konnte. 🙂
Um das Thema schnell und leicht verständlich zu erklären sind wir, trotz der eher unwahrscheinlichen Werte, lieber bei einfacheren Zahlen und Ergebnissen geblieben.
Liebe Grüße!