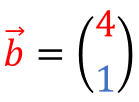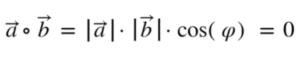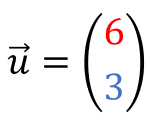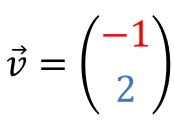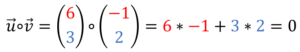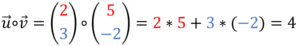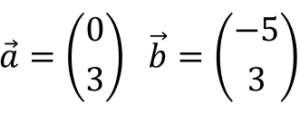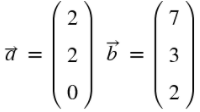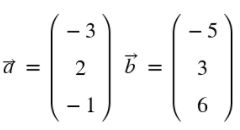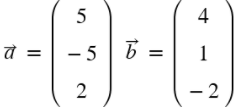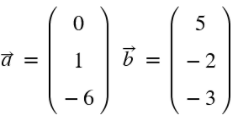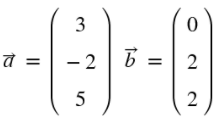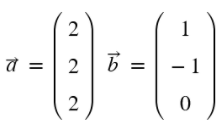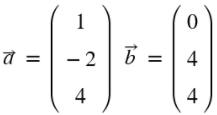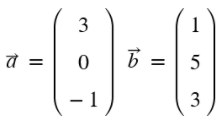Vor dem Fach Mathe scheuen sich viel Schüler. Wenn dann noch das Thema Skalarprodukt von Vektoren aufkommt, schalten die meisten ab. Aber in Wirklichkeit ist es gar nicht so kompliziert. In diesem Artikel erklären wir dir leicht verständlich…
- die Definition vom Skalarprodukt ist und wie man es berechnet
- wie man Winkel zwischen Vektoren bestimmen kann
- Aufgaben zum Üben
Lass uns direkt anfangen!
Berechnung Skalarprodukt zweier Vektoren – so wird´s gemacht
Berechnet wird es durch Addition der zeilenweise Produkte.
Die Formel dafür lautet:
Natürlich kannst du es auch von Vektoren in der Ebene berechnen:
Anwendung Skalarprodukt
Mithilfe des Skalarproduktes können einige Aufgaben gelöst werden, wenn es um Vektoren geht.
Schnittwinkel zweier Vektoren
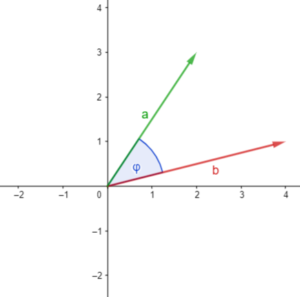
Anwendung findet es bei der Bestimmung der geometrischen Lage eines Vektors. Denn mithilfe des Skalarprodukt kannst du den Winkel zwischen zwei Vektoren berechnen.
Hier siehst du die Vektoren dargestellt. Mithilfe der Formel kannst du den eingeschlossenen Winkel φ berechnen.
senkrechte Vektoren – schnelle Berechnung
Du kannst auch prüfen, ob zwei Vektoren orthogonal zueinander liegen. Dafür gilt:
Das Produkt zweier Vektoren muss also 0 ergeben.
Damit dieser Fall eintritt, muss einer der Faktoren = 0 sein.
Da die Länge der Vektoren immer größer als null ist, muss der cos(φ) = 0 sein. Bei einem Winkel von 90° ist das der Fall.
Aus diesem Grund verlaufen die Vektoren orthogonal (senkrecht) zueinander bei dem Ergebnis von 0.
Skalarprodukt Aufgaben zum selber lösen
Wir haben dir noch ein paar Rechenaufgaben herausgesucht. Damit kannst du dein erarbeitetes Wissen unter Beweis stellen. Das wird dir in den nächsten Mathestunden sicherlich helfen!
a)
b)
c)
Lösung
a) = 9
b) = 20
c) = 15
a)
b)
c)
Lösung
a) = 70,93°
b) = 64,74°
c) = 69,87°
a)
b)
c)
Lösung
a) senkrecht
b) nicht senkrecht
c) senkrecht
Wenn dir der Artikel gefallen hat und du noch mehr zum Thema Mathematik wissen willst, solltest du dir auch die Artikel zu linearen Gleichungen und zur Prozentrechnung anschauen.

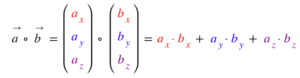
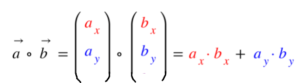
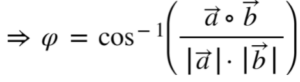
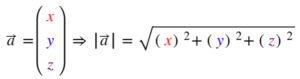
 und
und