5,00 von 5 Sterne
Loading...
Sinus, Cosinus, Tangens? Was ist das denn nochmal? Und dann auch noch die Sinusfunktion und und und…
Naja, eigentlich ist es recht simpel, man muss es nur einmal verstanden haben.
Und genau das erklären wir dir jetzt, damit auch du es schaffst sie zu unterscheiden und richtig einzusetzen!
In der Trigonometrie geht es um die Beziehungen zwischen den Seiten und Winkeln in einem rechtwinkligen Dreieck.
Ein rechtwinkliges Dreieck hat einen rechten Winkel (90 Grad), während die beiden anderen Winkel kleiner als 90 Grad sind.
Die Seite, die dem rechten Winkel gegenüberliegt, wird als Hypotenuse bezeichnet, während die anderen beiden Seiten als Katheten bezeichnet werden.
Wenn wir uns auf eine der beiden Katheten beziehen, können wir den Winkel zwischen dieser Kathete und der Hypotenuse betrachten. Wir nennen diesen Winkel Alpha (α).
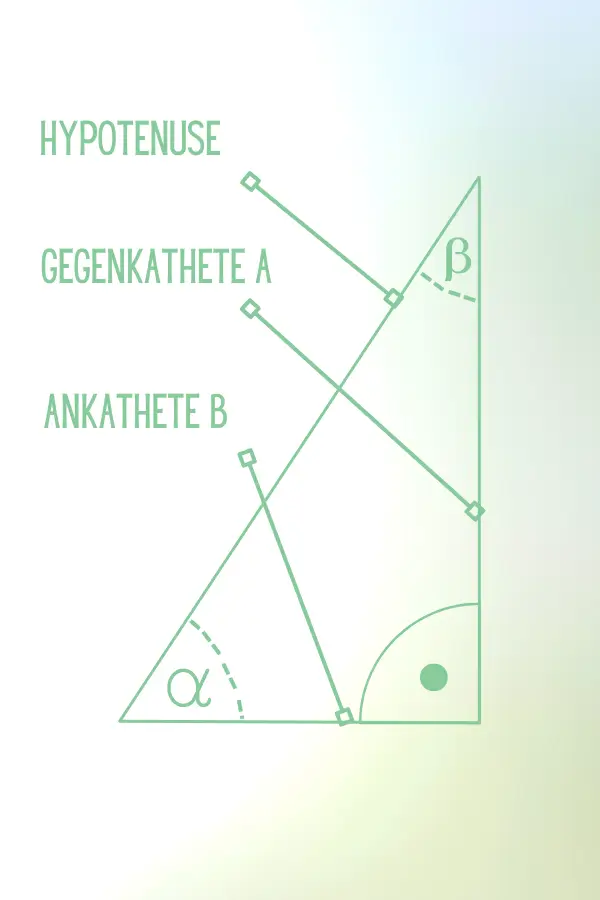
Die trigonometrischen Funktionen Sinus, Cosinus und Tangens sind mathematische Werkzeuge, die uns helfen, die Beziehungen zwischen den Winkeln und Seiten in einem rechtwinkligen Dreieck zu berechnen.
Diese Funktionen werden häufig in Berechnungen und Formeln in der Mathematik, der Physik, der Ingenieurwissenschaften und anderen Bereichen verwendet.
Sinus – einfach erklärt
Die Sinusfunktion ist eine periodische mathematische Funktion, die das Verhältnis der Länge der Gegenkathete zu der Länge der Hypotenuse eines Dreiecks beschreibt.
Mathematisch ausgedrückt, ist der Sinus von einem Winkel definiert als das Verhältnis der gegenüberliegenden Seite (Gegenkathete) zur Hypotenuse des rechtwinkligen Dreiecks.
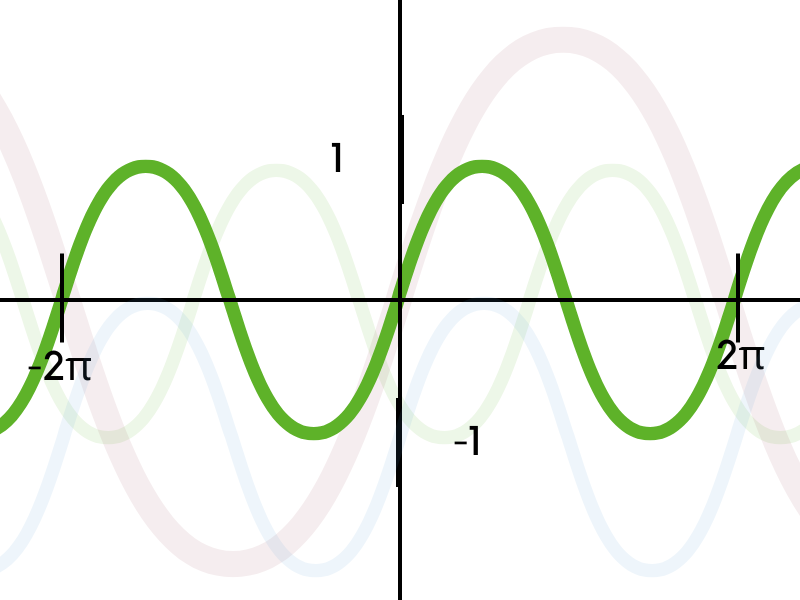
Die Sinusfunktion hat eine Wellenform und eine Periode von 2π (2 Pi), was bedeutet, dass sich die Funktion nach jeder Distanz von 2π wiederholt.
Die Sinusfunktion hat auch eine Amplitude, die die maximale Auslenkung der Funktion von ihrem Mittelwert beschreibt.
Die Sinusfunktion wird in vielen Bereichen der Mathematik und der Physik verwendet, insbesondere in der Beschreibung von periodischen Phänomenen wie Schall- und elektromagnetischen Wellen sowie in der Berechnung von Bewegungen, Schwingungen und Oszillationen.
Damit du dir diese Komplexität einfach vorstellen kannst, lass uns die Sinusfunktion einfach zeichnen. Dann ist sie gar nicht mehr so kompliziert, wie sie auf den ersten Blick wirkt.
Sinusfunktion Ableitung
Die Sinusfunktion abzuleiten ist besonders einfach. Eigentlich musst du dir das nur merken, wobei es auch in den meisten Formelsammlungen steht 😉
Parameter der Sinusfunktion
Wir untersuchen zunächst den Parameter d, welcher die Sinuskurve je nach Vorzeichen entweder nach oben (falls d > 0) oder nach unten (falls d < 0) verschiebt.
Je nach Vorzeichen verschiebt der Parameter c die Sinuskurve entweder nach links (falls c > 0) oder nach rechts (falls c < 0). Allerdings sind die Vorzeichen im Falle der Verschiebung in x-Richtung nicht so intuitiv wie im Falle der Verschiebung in y-Richtung.
Der Parameter a beeinflusst die Amplitude der Sinuskurve und dehnt sie aus (wenn |a| > 1) oder staucht sie zusammen (wenn |a| < 1) entlang der y-Achse. Mit anderen Worten, der Parameter a streckt oder staucht die Sinuskurve entlang der y-Richtung.
Abschließend betrachten wir die Auswirkungen des Parameters b. Wenn |b|< 1, wird die Sinuskurve entlang der x-Richtung gestreckt, während sie bei |b| > 1 gestaucht wird. Die nachfolgende Abbildung veranschaulicht diese Situation grafisch.
Cosinus – einfach erklärt
Der Cosinus ist eine trigonometrische Funktion, die in der Geometrie verwendet wird, um fehlende Winkel oder Seiten in einem rechtwinkligen Dreieck zu berechnen.
Mathematisch ist der Cosinus das Verhältnis der Länge der Ankathete zu der Länge der Hypotenuse des Dreiecks.
Mit einem geometrischen Trick, bei dem der Einheitskreis ins Spiel kommt, lässt sich die Definition des Cosinus auf eine größere Ebene erweitern.
Hierbei gibt der Cosinus die x-Koordinate eines Punktes auf dem Einheitskreis an. Durch das Periodizitätsprinzip des Kreises, lässt sich dadurch eine periodische Funktion konstruieren, die Cosinusfunktion genannt wird.
Cosinusfunktion
Die Cosinusfunktion ist eine periodische mathematische Funktion, die auf dem Einheitskreis definiert ist.
Sie beschreibt das Verhalten der x-Koordinate eines Punktes, der sich auf dem Einheitskreis mit dem Radius 1 bewegt.
Mathematisch ist die Cosinusfunktion definiert als das Verhältnis der Länge der Ankathete zu der Länge der Hypotenuse eines rechtwinkligen Dreiecks.
Die Cosinusfunktion verhält sich ähnlich wie die Sinusfunktion, hat allerdings den Hochpunkt bei x=0.
Cosinusfunktion am Koordinatensystem
Parameterfunktion von Cosinus
Die Verschiebung der Cosinusfunktion verhält sich genau wie bei der Sinusfunktion und kannst du oben ablesen.
Tangens – einfach erklärt
Im rechtwinkligen Dreieck kann der Tangens genutzt werden, um fehlende Seiten und Winkel zu berechnen. Er wird definiert als das Verhältnis der Gegenkathete zur Ankathete eines Winkels.
Tangensfunktion
Nachfolgend sind die wesentlichen Merkmale des Tangens-Graphen aufgelistet:
- Der Tangens-Graph hat die gleichen Nullstellen wie der Sinus-Graph (…,-3π, –2π, –π, 0, π, 2π, 3π,…).
- Die Definitionslücken des Tangens-Graphen entsprechen den Nullstellen des Cosinus-Graphen (…,-\frac{2}{3}π, −2π, 2π, \frac{2}{3}π, …).
- Der Tangens-Graph hat keine Extremstellen.
- Der Tangens-Graph ist punktsymmetrisch.
Der Graph der Tangensfunktion sieht übrigens so aus:
Jetzt wo wir zusammen den Sinus, Cosinus und Tangens durchgegangen haben, lass uns doch eine Beispielaufgabe zusammen rechnen, bevor du dann selbst probieren kannst eine Übungsaufgabe zu lösen!
Übungsaufgabe Trigonometrie
Und jetzt löse doch folgende Aufgabe noch für dich alleine! Mit Lösung
Ein Turm ist 30 Meter hoch.
Ein Feuerwehrmann steht am Fuß des Turms und will eine Leiter gegen den Turm lehnen, um einen Mann zu retten, der auf dem Dach festsitzt.
Die Leiter soll einen Winkel von 60 Grad mit dem Boden bilden.
Wie lang muss die Leiter sein, damit der Feuerwehrmann den Mann auf dem Dach retten kann?
Lösungsweg:
Um die Länge der Leiter zu berechnen, können wir die Sinus-Definition verwenden:
sin(60°) = gegenüberliegende Seite / Hypotenuse
sin(60°) = 30 / Hypotenuse
Wir können diese Gleichung nach der Hypotenuse (also der Länge der Leiter) auflösen:
Hypotenuse = 30 / sin(60°)
Hypotenuse = 34,64
Die Leiter muss also mindestens 34,64 Meter lang sein, damit der Feuerwehrmann den Mann auf dem Dach retten kann.
FAQ Sinus Cosinus Tangens
Was sind Sinus, Cosinus und Tangens?
Sinus, Cosinus und Tangens sind trigonometrische Funktionen, die in der Geometrie verwendet werden, um Verhältnisse von Seiten und Winkeln in rechtwinkligen Dreiecken zu berechnen.
Wie berechnet man Sinus, Cosinus und Tangens?
Der Sinus eines Winkels ist das Verhältnis der Länge der Gegenkathete zur Länge der Hypotenuse, der Cosinus eines Winkels ist das Verhältnis der Länge der Ankathete zur Länge der Hypotenuse, und der Tangens eines Winkels ist das Verhältnis der Länge der Gegenkathete zur Länge der Ankathete.
Wofür werden Sinus, Cosinus und Tangens verwendet?
Sinus, Cosinus und Tangens werden in vielen Anwendungen der Mathematik und Naturwissenschaften verwendet, wie z.B. bei der Berechnung von Kräften, Winkeln und Distanzen in der Physik, bei der Berechnung von Frequenzen und Schwingungen in der Akustik und Elektrotechnik und bei der Berechnung von Distanzen und Winkeln in der Navigation und Geodäsie.
Was ist der Einheitskreis?
Der Einheitskreis ist ein Kreis mit dem Radius 1, der um den Ursprung eines Koordinatensystems gezeichnet wird. Der Einheitskreis wird oft verwendet, um Sinus, Cosinus und Tangens von Winkeln zu berechnen, indem man den Winkel als Bogenlänge auf dem Kreis betrachtet.
Was ist die Periodizität von Sinus, Cosinus und Tangens?
Sinus, Cosinus und Tangens sind periodische Funktionen, das bedeutet, dass sie sich nach einem bestimmten Wert in regelmäßigen Abständen wiederholen. Die Periodizität des Sinus und Cosinus ist 2π, das bedeutet, dass sie sich alle 2π Radiant oder 360 Grad wiederholen. Der Tangens hat eine Periodizität von π oder 180 Grad.
Was sind die Nullstellen von Sinus, Cosinus und Tangens?
Die Nullstellen von Sinus und Cosinus sind alle Vielfachen von π oder 180 Grad, also …, -2π, -π, 0, π, 2π, … Die Nullstellen des Tangens sind alle Vielfachen von π/2 oder 90 Grad, also …, -3π/2, -π/2, π/2, 3π/2, …
Ich hoffe, diese FAQ helfen dir weiter!
Wir haben viel Mühe in diesen Artikel gesteckt und freuen uns riesig, wenn du uns eine Sternebewertung und einen Kommentar hinterlässt. Vielen Dank!
5,00 von 5 Sterne
Loading...
Hab die Schule schon lange hinter mir.
Das hier ist eine tolle Auffrischung. Vielen Dank!!