4,47 von 5 Sterne
Loading...
Ganze Zahlen, reelle Zahlen, rationale Zahlen… langsam kommst du durcheinander, welche Zahlen jetzt genau was sind?
In diesem Artikel grenzen wir die verschiedenen Themen voneinander ab und erklären, was es mit den rationalen Zahlen auf sich hat. Danach zeigen wir dir, wie man mit dieser Zahlenart die unterschiedlichen Rechnungen macht.
Los geht’s!
Allgemein kann man sagen, dass jede Zahl die als Bruch von zwei ganzen Zahlen dargestellt werden kann, eine rationale Zahl ist.
Zu den natürlichen Zahlen (ℕ) und den ganzen Zahlen (ℤ) kommen nun also mit den rationalen Zahlen auch die Brüche hinzu.
Das rationale Zahlen Zeichen ist ℚ.
Hier sind nochmal alle verschiedenen Zahlenmengen dargestellt:
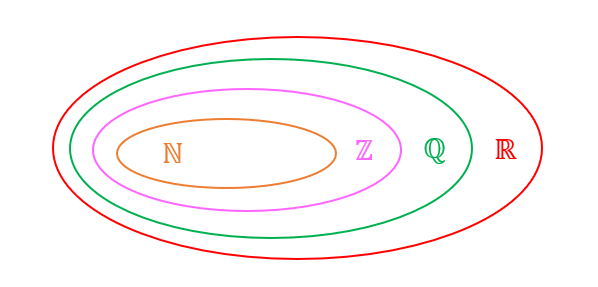
ℕ steht für die natürlichen Zahlen. Diese sind in den ganzen Zahlen ℤ beinhaltet, welche wiederum Elemente in den rationalen Zahlen ℚ sind. Die rationalen Zahlen sind Teil der reellen Zahlen ℝ.
Rationale Zahlen Beispiele
Natürliche und ganze Zahlen sind Teil der rationalen Zahlen, weil du sie als unechte Brüche (5/1=5, 23/1=23) schreiben kannst.
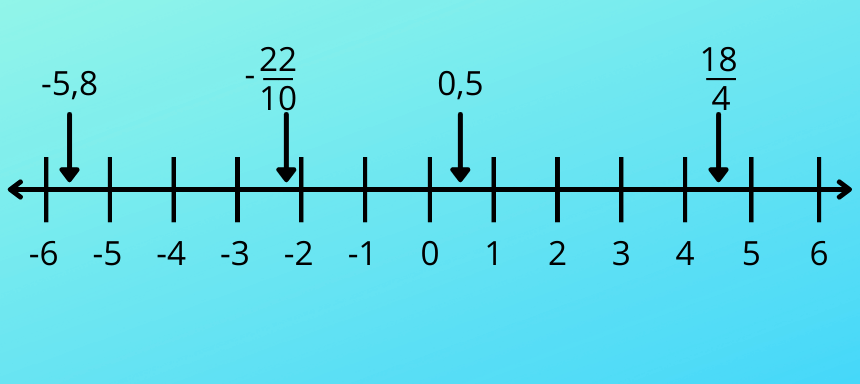
Oben sieht man ein paar Beispiele von Dezimalzahlen und Brüchen, wie sie in einem Zahlenstrahl eingetragen werden würden.
Rationale Zahlen addieren und subtrahieren
Da rationale Zahlen nichts anderes als ganze Zahlen und Bruchzahlen sind, kann man ganz normal alle Grundrechenarten (addieren, subtrahieren, multiplizieren, dividieren) anwenden.
Bei dem Addieren und Subtrahieren von Brüchen kommt es darauf an, einen gemeinsamen Nenner zu finden und den Zähler anschließend zu addieren oder zu subtrahieren.
Beispiel mit Addition
Beispiel mit Subtraktion
Rationale Zahlen multiplizieren und dividieren
Beim Multiplizieren und Dividieren von Brüchen geht man ein wenig anders vor!
Beispiel mit Multiplikation
Bei der Multiplikation muss man nicht auf einem gemeinsamen Nenner kommen, sondern multipliziert beide Brüche direkt.
Beispiel mit Division
Beim Dividieren muss man den ersten unveränderten Bruch mit dem Kehrwert des Zweiten multiplizieren.
Rationale Zahlen Rechner
Wenn du mal keine Lust oder Zeit hast einen Bruch selbst zu berechnen, kannst du auch einfach die vorhandenen Zahlen auf folgender Seite eingeben und dir das Ergebnis errechnen lassen: Der Bruch Rechner zum einfachen Berechnen!
Rationale Zahlen Übungen
In diesem Abschnitt findest du nochmal ein paar Übungsaufgaben zum Berechnen von rationalen Zahlen (Brüchen).
Wenn du die Lösung wissen möchtest, kannst du ganz einfach auf das Kästchen klicken!
⅚ + ⅗ = ?
43/30 = 1 13/30
2/2 + 7/4 = ?
11/4 = 2 ¾
4/3 - 5/9 = ?
7/9
16/20 - ⅗ = ?
⅕
3/2 * 3/7 = ?
9/14
⅖ * ½ = ?
2/10 = ⅕
½ : 1/6 = ?
3/1 = 3
4/3 : 5/7 = ?
28/15 = 1 13/15
Übersichtstabelle Zahlenarten
Damit du einen besseren Einblick bekommst, was es für unterschiedliche Zahlenarten gibt, haben wir dir hier eine kleine Übersicht erstellt, die du auch für dich Herunterladen kannst!
Zahlenart | Symbol | Beispiel |
Natürliche Zahlen | ℕ | { 0, 1, 2…} |
Ganze Zahlen | ℤ | { …-1, 0, 1…} |
Rationale Zahlen | ℚ | {...-2/5, -1, 0, 1, 1/3…} |
Reelle Zahlen | ℝ | { …-1/3, 1, 0, 1, 2,3...} |
FAQ – Häufig gestellte Fragen
Zum Schluss haben wir dir die häufig gestellten Fragen rund um diese Zahlenart zusammengestellt, damit du nochmal einen guten Überblick hast!
Was sind rationale Zahlen einfach erklärt?
Allgemein kann man sagen, dass jede Zahl die als Bruch von zwei ganzen Zahlen dargestellt werden kann, eine rationale Zahl ist. Das Zeichen für die rationalen Zahlen ist ℚ.
Was ist eine rationale Zahl Beispiel?
Jede natürliche Zahl ist eine rationale Zahl (z.B. 13). Jede Ganze Zahl ist eine rationale Zahl (z.B. -7). Jeder dieser Zahlen kann als unechter Bruch dargestellt werden und ist deswegen auch eine rationale Zahl.
Was gehört nicht zu den rationalen Zahlen?
Irrationale Zahlen gehören nicht zu den rationalen Zahlen. Eine irrationale Zahl kann nicht als Quotient zweier ganzer zahlen dargestellt werden. Hierzu zählen beispielsweise die Wurzeln aus natürlichen zahlen, die keine Quadratzahlen sind. Eine weitere irrationale Zahl ist die Kreiszahl Pi (π).
Wie sieht das Zeichen für rationale Zahlen aus?
Das Zeichen für rationale Zahlen ist ℚ.
Erst einmal sind wir dir sehr dankbar, dass du unseren Artikel bis hierhin gelesen hast. 🙂
Bevor du uns verlässt, wäre es echt cool, wenn du uns noch schnell einen Kommentar hinterlassen könntest!
Wir verbringen viel Zeit damit, die Artikel bestmöglich auf euch abszustimmen.
Wenn du dir also schnell eine Sekunde Zeit nehmen könntest, wäre es toll wenn du uns noch eine Sternebwertung hinterlassen könntest.
Danke!?
4,47 von 5 SterneLoading...
