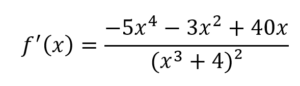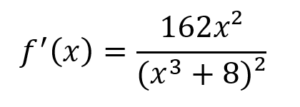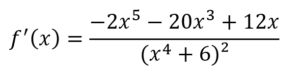5,00 von 5 Sterne

Wie leitet man eigentlich eine Funktion ab, die im Bruch steht?
Das ist nicht immer so einfach – viele Schüler und Schülerinnen haben Schwierigkeiten damit.

Wir zeigen dir in diesem Artikel step by step, wie du die Quotientenregel beim Ableiten von Funktionen anwendest, damit du immer den Durchblick behältst!

Inhalt

So funktioniert die Quotientenregel

Die Quotientenregel wendest du erst an, wenn du eine bestimmte Funktion im Bruch vor dir liegen hast. Siehe dir dazu die untere Abbildung an. Wir haben also einen Zähler und einen Nenner und wenn du so einen Ausdruck ableiten möchtest, brauchst du eine spezielle Regel.

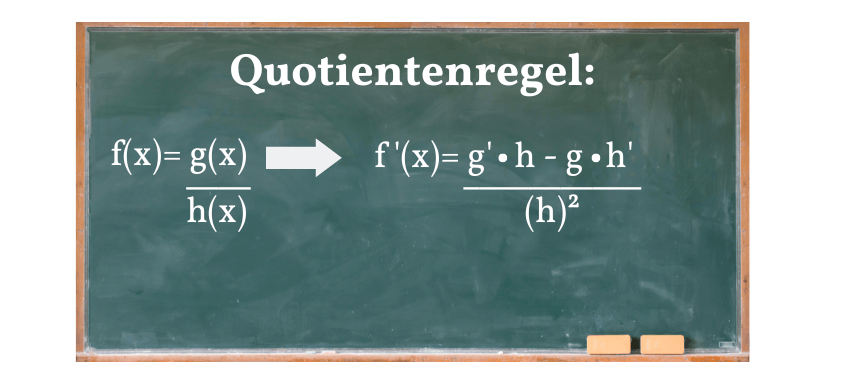
Diese Regel ist die Quotientenregel – du siehst sie in der Abbildung. Von allen Ableitungsregeln ist diese Regel mit am schwierigsten zu verstehen. Aber auch die werden wir gemeinsam meistern!

Kommen wir zur unserer Beispielaufgabe. Diese werden wir zusammen durchgehen und ableiten.

Schritt 1

Wir lesen als Erstes aus der Beispielfunktion, was unser g(x) und h(x) ist. g(x) ist immer der Zähler, das heißt was oberhalb des Bruchstriches steht, also x²+3. h(x) ist dann dementsprechend der Nenner, also hier x³+2x.

Schritt 2

Nun bilden wir die erste Ableitung von g(x) und h(x). Wenn wir g(x), also x²+3, ableiten, erhalten wir 2x. Das gleiche nun für h(x)=x³+2x, abgeleitet wird es zu h'(x)=3x²+2.

Schritt 3

In diesem Schritt wenden wir auch schon die Quotientenregel an. Dazu schauen wir uns die Regel in der Abbildung an und notieren uns f'(x)=2x * (x³+2x) – (x²+3) * (3x+2) / (x³+2)²

Vergiss nicht, die Klammern zu setzen – sonst gilt Punkt vor Strich Rechnung und wir kommen auf ein anderes Ergebnis.

Das Ganze ist schon die Ableitung. Wir vereinfach das alles aber nochmal, damit es besser aussieht. Wir lösen im Zähler erst die Klammer auf. Du weißt “irgendwas” mal Klammer heißt, alles was in der Klammer ist mit dem Ausdruck davor multiplizieren.

Das heißt, die erste Rechnung ist 2x * (x³+2x). 2x* x³ ergibt zusammen 2x^4.Den ersten Teil haben wir schon ausgerechnet, kommen wir zum zweiten Teil. Da rechnen wir 2x * 2x und das ergibt dann 4x²

Kommen wir nun zum hinteren Teil. Da schauen wir uns das Vorzeichen an, negativ * positiv ist negativ. Wollen wir (x²+3)*(3x+2) ausklammern, so rechnen wir zuerst x² * 3x= 3x³ , dann x²* 2= 2x². Danach mit der 3* 3x= 9x und 3*2=6.

Zusammengefasst würde der Zähler so aussehen: 2x⁴ + 4x² – (3x³+2x²+9x+6). Den können wir weiter kürzen zu 2x⁴ -3x³ +2x²-9x-6. Beachte das Vorzeichen vor der Klammer. Im Nenner verändert sich nicht viel, außer dass wir h(x) quadrieren. Das wird dann zu (x³+2)².