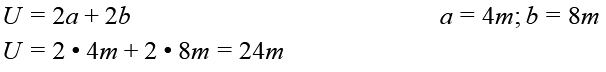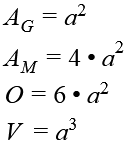4,67 von 5 Sterne
Loading...
Du möchtest unbedingt wissen, wie man ganz leicht die Oberfläche und das Volumen eines Quaders berechnen kann? Dann bist du hier genau richtig. Wir erläutern dir die wichtigsten Formeln um einen Quader zu berechnen. Festige dein Wissen mit unseren Übungsaufgaben und kontrolliere diese anschließend.
Fangen wir direkt an!
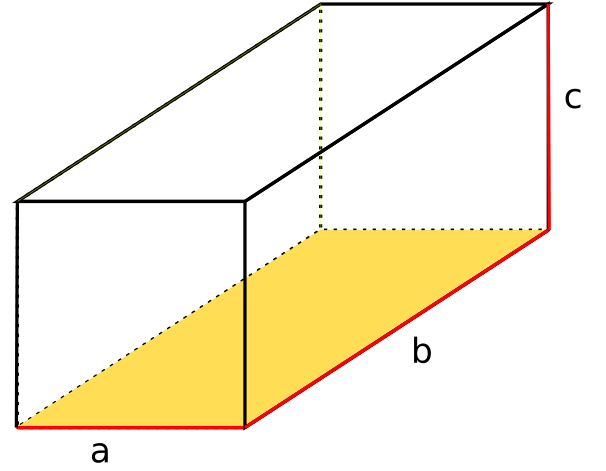
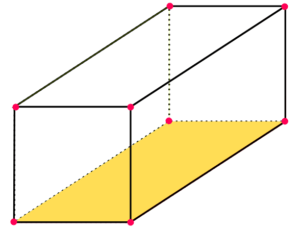
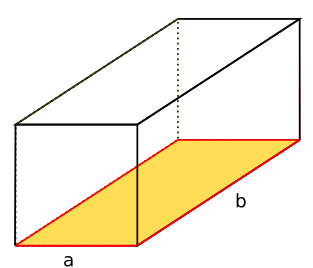
Ein Quader gehört wie eine Pyramide und eine Kugel zu den geometrischen Körpern. Er wird aus insgesamt sechs Rechtecken zusammengesetzt, die rechtwinklig (orthogonal) zueinander angeordnet sind. Zudem kann man eine Raumdiagonale bestimmen, die jeden Eckpunkt der Grundfläche mit dem am weitesten entfernten und gegenüberliegenden Eckpunkt der Deckfläche verbindet.
Ein Quader hat 8 Ecken und 12 Kanten, von denen jeweils 4 die gleichen Längen besitzen. Die gegenüberliegenden Flächen, die parallel zueinander liegen, sind kongruent (deckungsgleich).
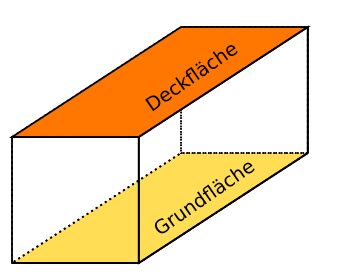
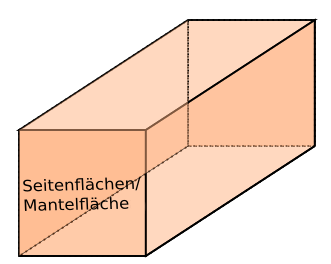
Zudem sollte dir bewusst sein, wie man die einzelnen Flächen vom Quader bezeichnet. Ein Quader hat eine Grundfläche und eine, der Grundfläche gegenüberliegende, Deckfläche. Die übrigen Flächen werden als Seitenflächen bezeichnet und ergeben die Mantelfläche.
Volumen Quader berechnen
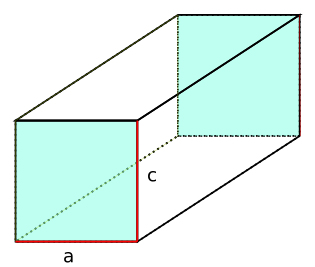
Um das Volumen einen Quaders zu berechnen, brauchst du die Angaben von den Kantenlängen a, b und c.
Zunächst wird der Flächeninhalt der Grundfläche berechnet:
Im Anschluss wird das Ergebnis mit der Höhe multipliziert. Die Höhe entspricht c:
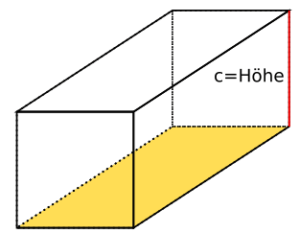
Wir erhalten also die folgende Formel zur Berechnung des Volumens:
Berechne die Höhe eines Pakets mit den Seitenlängen a=40cm und b=60cm und dem Volumen V=720cm².
Zunächst setzt du einfach alle Werte in die Gleichung ein, die du schon kennst, und löst dann die Gleichung nach c auf.
Das Paket hat eine Höhe von 3cm.
Quader Fläche berechnen
Die Oberfläche eines Quaders setzt sich aus den Flächeninhalt der vier Seitenflächen bzw. der Mantelfläche sowie dem Flächeninhalt der Grund- und Deckfläche zusammen.
Daraus ergibt sich folgende Formel:
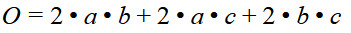
Wenn du genau wissen möchtest, wie sich die Formel zusammensetzt, dann schau dir die nächsten zwei Unterkapitel genauer an.
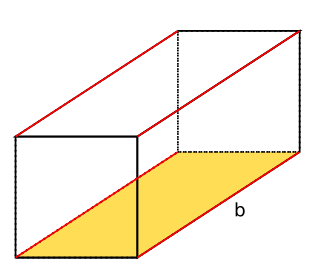
Mantelfläche berechnen
Die Mantelfläche (M) eines Quaders beschreibt die vier Seitenflächen ohne Grund- und Deckfläche. Sie besteht also aus zwei Paaren deckungsgleicher Rechtecke.
Um das erste Paar der Rechtecke zu berechnen benötigst du die Seitenlängen a und c. Dadurch, dass beide Flächen berechnet werden müssen, nimmst du den Flächeninhalt zweimal:
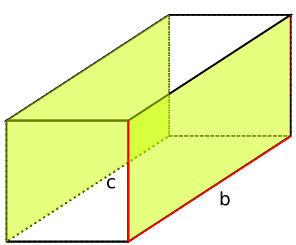
Im nächsten Schritt berechnest du das weitere Paar von Rechtecken wie zuvor:
Es ergibt sich folgende Formel zur Berechnung der gesamten Mantelfläche:
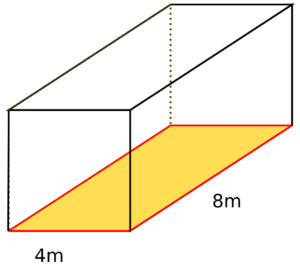
Gerhardt möchte seine Wände streichen. Dafür hat er sein rechteckiges Zimmer ausgemessen: Die längste Wand ist 8m und die kürzeste 4m lang.
Die Wände sind 2,5m hoch. Mit einem Eimer Farbe kann Gerhard 20m² streichen. Wie viele Eimer muss Gerhard auf seine Einkaufsliste schreiben?
Setze alle bekannten Größen in die Formel ein und rechne dann die Mantelfläche aus:
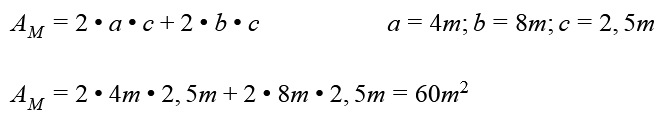
Im nächsten Schritt überlegst du, wie viele Eimer (x) Gerhard braucht, damit er am Ende 
Wand bemalen kann.
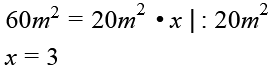
Gerhardt sollte insgesamt 3 Eimer Farbe auf seine Einkaufsliste schreiben.
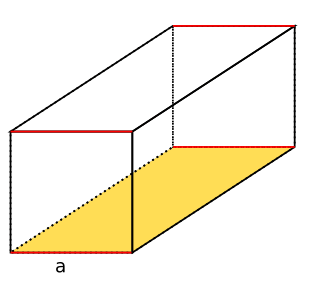
Grundfläche und Deckfläche berechnen
Die Grundfläche bzw. Deckfläche (AGD) kannst du nun mithilfe der Seitenlängen von a und b berechnen. Wie zu erkennen ist, sind diese Flächen deckungsgleich, sodass du die Summe aus Boden- und Deckfläche mit folgender Formel erhältst:
Um die gesamte Oberfläche eines Quaders zu berechnen, fügst du nun die Formeln zur Berechnung der Mantelfläche und die der Grund- und Deckfläche zusammen:
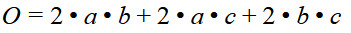
Anna möchte ihr rechteckiges Arbeitszimmer neu tapezieren. An alle Wände und die Decke soll eine warmweiße Tapete. Wie viel m² Tapete sollte Anna bestellen, wenn der Raum folgende Maße hat: 10m x 4,5m x 2,4m?
Bevor du alle vorgegebenen Angaben in die Formel einsetzt, sollte dir klar sein, dass der Boden nicht tapeziert wird. Die Grundfläche also von der Oberflächenformel für einen Quader sollte herausgenommen werden. Daraus ergibt sich folgende Gleichung:
a= 4,5m
b= 10m
c= 2,4m
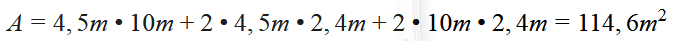
Anna braucht 
Tapete für ihr Arbeitszimmer.
Umfang Quader berechnen
Um den Umfang eines Quaders zu berechnen, addierst du einfach alle Seitenlängen zusammen.
Die Formel lautet:
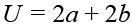
Gerhardt hat seine Wände gestrichen und würde gerne eine Fußleiste am Übergang von der Wand zum Boden anbringen. Wie viel m Leiste sollte er bestellen?
Zur Erinnerung: Die längste Wand in seinem quadratischen Zimmer ist 8m und die kürzeste 4m lang. Die Wände sind 2,5m hoch.
Zur Berechnung des Umfangs benötigen wir die Angaben der Seitenlängen a und b.
Die Höhe brauchen wir also gar nicht. Wir rechnen:
Gerhardt sollte 24m Fußleiste bestellen.
Quader Formeln – Übersicht
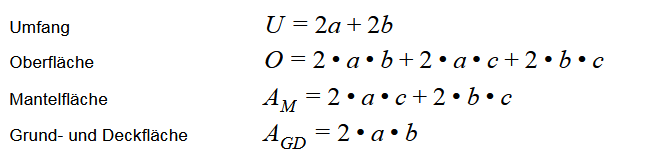
Quader berechnen – FAQ
Ist ein Würfel ein Quader?
Ein Würfel ist eine spezielle Arte eines Quaders. Ein Würfel hat nämlich überall die gleiche Seitenlänge, sodass er aus 6 deckungsgleichen Quadraten besteht. Es müssen keine Seitenlängen mehr mit a, b und c unterschieden werden. Du kannst mit diesen stark verkürzten Formeln rechnen:
Wie viele Ecken hat ein Quader?
Ein Quader hat 8 Ecken.
Wie viele Kanten hat ein Quader?
Ein Quader hat 12 Kanten.
Wie viele Flächen hat ein Quader?
Ein Quader besteht aus sechs Flächen, die rechtwinklig aufeinander stehen. Man unterscheidet die Grundfläche von der Mantelfläche und der Deckfläche.
Wir hoffen sehr, dass dir dieser Beitrag weiterhelfen konnte. Falls du noch Schwierigkeiten mit manchen Aufgaben haben solltest, schreib uns deine Fragen gerne in die Kommentare.
Falls du wissen möchtest, wie man die Raumdiagonale eines Quader bestimmen kann, sieh dir diesen Artikel an. Solltest du dich dafür interessieren, wie man andere geometrische Körper berechnet, schau mal bei unserem Beiträgen zu Kugeln und Zylindern. Hier erfährst du, wie du Brüche ganz einfach und schnell multiplizierst oder addierst.
Kommentiere gerne mal die Farbe, in der du am liebsten dein Zimmer streichen würdest! 😉
