5,00 von 5 Sterne
Loading...
Du behandelst gerade im Matheunterricht die proportionale Zuordnung und hast aber nicht ganz verstanden, wie du sie in den Aufgaben erkennen und anwenden kannst?
Dies ändern wir in wenigen Minuten, denn durch eine einfache Aufklärung der verschiedenen Darstellungsformen und Berechnungen, mit jeder Menge Beispiele, wirst du die proportionale Zuordnung meistern.
Dann, nichts wie los!
Bei einer proportionalen Zuordnung stehen zwei Variablen in einer Beziehung, bei der sich eine Größe proportional zur anderen Größe verändert. Denn das bedeutet, wenn sich eine Größe ändert, ändert sich die andere Größe im gleichen Verhältnis dazu.
Für die Schüler, welche die proportionale Zuordnung schon kennen, gibt es auch noch die antiproportionale Zuordnung, die euch interessieren könnte.
Proportionale Zuordnung ein alltägliches Geschehen- Beispiel
Im Alltagsleben begegnest du oft einer proportionalen Zuordnung. Dabei teilst du in gleichmäßigen Abständen eine Zahl oder eine Menge einer anderen Zahl oder Menge hinzu, was auch als proportionales Wachstum bezeichnet wird.
So siehst du beim Beispiel, dass wir einen Wert (Brezel) zu einem anderen Wert (Preis) geordnet haben.
Proportionale Zuordnung in einer Wertetabelle berechnen
Die Wertetabelle der proportionalen Zuordnung hat zwei Zeilen. In der oberen Zeile werden die x-Werte bzw. unabhängige Variable eingetragen, während in der unteren Zeile sich die zugeordneten y- Werte bzw. abhängige Variablen befinden.
Proportionale Zuordnung – Proportionalitätsfaktor
Zu einer proportionalen Zuordnung gehört immer ein Proportionalitätsfaktor. Es ist die Zahl, die angibt, um welchen Faktor sich der y-Wert ändert, basierend auf der Entwicklung des x-Werts. Du erhältst den Proportionalitätsfaktor durch die Formel: p= y-Wert/ x-Wert
Schauen wir uns nochmal das Beispiel mit der Dinnerparty an:
Wie du siehst, bekommst du mit jeder Rechnung, in der du den Y-Wert mit dem X-Wert dividierst, das gleiche Ergebnis. Dieses Phänomenen wird auch Quotientengleichheit genannt. Der Proportionalitätsfaktor beträgt somit 4.
Mit Dreisatz berechnen
Wenn du weißt, dass dir eine proportionale Zuordnung vorliegt, kannst du auch mit dem Dreisatz die fehlenden Werte leicht berechnen.
Nina fährt zur Tankstelle, um den Treibstoff für ihr Auto aufzufüllen. Ein voller Tank ihres Autos braucht 50 Liter und kostet 90 €. Jetzt möchte sie nur 35 Liter auftanken und möchte wissen, wie viel das kosten würde.
Was ist hierbei, der Proportionalitätsfaktor?
Proportionalitätsfaktor= 90 : 50 L = 1,8 L
Proportionalen Zuordnung: Fehlende Werte der Wertetabelle berechnen
Manchmal musst du auch eine proportionale Wertetabelle vervollständigen, und das funktioniert so:
Als Graph Schrittweise erklärt
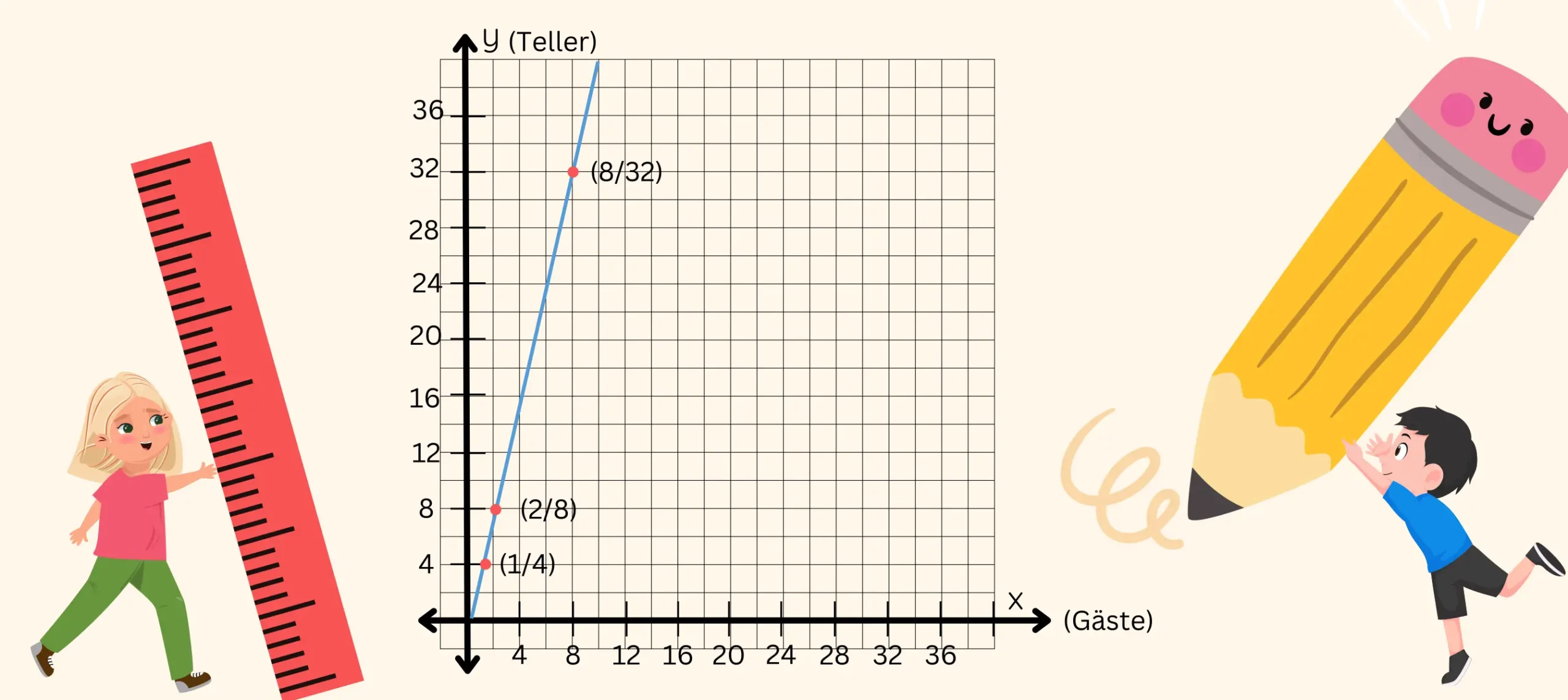
Du kannst die proportionale Zuordnung in einem Graphen darstellen, indem du die y-Werte und x-Werte aus der Tabelle herausnimmst und diese Punkte in einem Koordinatensystem einträgst.
In einem Koordinatensystem für proportionale Zuordnung repräsentiert die X-Achse die Ausgangswerte (unabhängige Variable), während die Y-Achse die zugeordneten Werte (abhängige Variable) darstellt.
Bei einer proportionalen Zuordnung ergibt das Verbinden der Punkte immer eine Ursprungsgerade mit dem Ursprung am Punkt (0/0), dabei verläuft die Gerade steigend von links nach recht. Für das Beispiel nehmen wir wieder die Beispielaufgabe von der Dinnerparty her.
Als Pfeildiagramm
Um die proportionale Zuordnung als Pfeildiagramm darzustellen, musst du einfach nur rechts neben dem Ausgangswert einen Pfeil einfügen und links davon die zugeordnete Zahl.
Die Gleichung – Zuordnungsvorschrift
Schließlich kannst du die proportionale Zuordnung auch in Form einer Gleichung zeigen, indem du ähnlich wie beim Pfeildiagramm den Proportionalitätsfaktor benutzt, außer dass der Pfeil mit einem Gleichsetzungszeichen ersetzt wird.
Übungsaufgaben – teste dich!
Ein Gärtner benötigt 8 Stunden, um 6 Gärten zu bewässern. Wie viele Gärten können von 8 Personen, 14 Personen oder 25 Personen in 3 Stunden bewässert werden?
Proportionaliätsfaktor= Anzahl der Gärten : Anzahl der Stunden = 6 : 1= 6
Anzahl der Personen | Bewässerte Gärten 8 Stunden |
1 | 6 |
2 | 12 |
6 | 36 |
25 | 150 |
Handelt es sich um eine proportionale Zuordnung? Begründe wieso?
Stunden | Anzahl der produ-zierten Produkte |
1 | 50 |
2 | 90 |
3 | 1201 |
4 | 140 |
Nein, es handelt sich nicht um eine proportionale Zuordnung, denn die Anzahl der produzierten Produkte sind nicht gleichmäßig mit der Anzahl der Stunden gestiegen. Beispielsweise kann man sehen, dass die Anzahl der produzierten Produkte in der ersten und zweiten Stunde um 40 gestiegen ist und die Anzahl zwischen der dritten und vierten Stunde um 20.
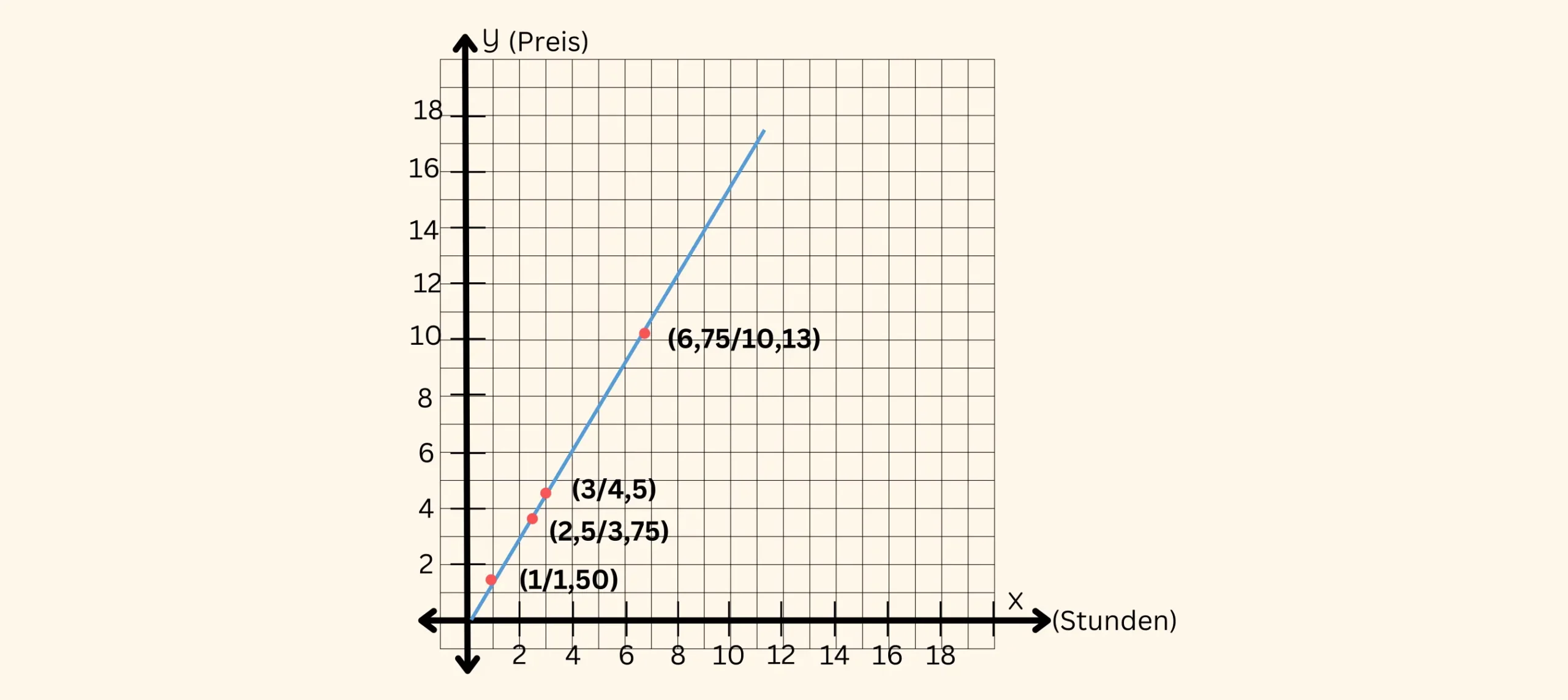
Im Schwimmbad kosten die Eintrittskarten für einen 9 Stunden Tagesbesuch jeweils 13,50 €. Wie hoch sind die Kosten, wenn eine Person 2 1/2, 3 oder 6 3/4 Stunden im Schwimmbad verbringt? Erstelle zum Schluss ein Koordinatensystem.
Dreisatz:
13,50 : 9= 1,50 €
1 Stunde kostet 1,50 € im Schwimmbad.
Wertetabelle:
Stunden im Schwimmbad | Kosten |
1 | 1,50€ |
2,5 | 3,75€ |
3 | 4,50€ |
6,75 | 10,13€ |
Wie kann ich überprüfen, ob es eine proportionale Zuordnung ist?
Wenn du den y-Wert durch den x-Wert dividierst, solltest du immer den gleichen Quotienten erhalten und so kannst du herausfinden, ob die Werte proportional zugeordnet sind.
Was ist die Formel der proportionalen Zuordnung?
Die Formel lautet: y (abhängige Variable) = Proportionalitätsfaktor • x (unabhängige Variable)
Wie nennt man den Graphen einer proportionalen Zuordnung?
Ein proportionaler Graph ist eine Ursprungsgerade, welcher am Punkt (0/0) steigend von links nach rechts verläuft, wobei es sich um eine lineare Funktion handelt.