Du verstehst einfach nur Bahnhof, wenn es um das Rechnen mit Potenzen geht?
Die Potenzgesetze zu kennen und anwenden zu können, ist von großer Bedeutung für das richtige Vereinfachen von Gleichungen.
Wir erklären dir in diesem Beitrag alle Regeln, die du beachten musst, um den Anschluss nicht zu verpassen. Damit du dein Wissen verfestigen kannst, findest du auch eine große Auswahl an Übungsaufgaben.
Los geht’s
Exponent, Basis und Potenz – Was ist was?
Mithilfe von Potenzen wird ausgedrückt, dass eine Zahl mehrere Male mit sich selbst multipliziert wird. Das Potenzieren ist seinem Ursprung nach eine abkürzende Schreibweise für eine wiederholte, mathematische Rechenoperation, deren Ergebnis die Potenz ist.
Dabei heißt die Zahl, die zu multiplizieren ist, Basis. Wie oft diese Basis als Faktor auftritt, wird durch den Exponenten angegeben.
Potenzregel spezieller Potenzen
- Jede Basis mit dem Exponenten 0 ist 1:
- Jede Basis mit dem Exponenten 1 ist die Basis:
- Die Basis 1 mit einem beliebigen Exponenten ist 1:
- Die Basis 0 mit einem beliebigen Exponenten ist 0:
Potenzen multiplizieren und dividieren
Um Potenzen multiplizieren und dividieren zu können, müssen sie mindestens die gleiche Basis oder den gleichen Exponenten haben. Wie du in dem jeweiligen Fall vorgehen musst, kannst du in den folgenden zwei Unterkapiteln lesen.
Potenzen mit gleicher Basis multiplizieren und dividieren
- Wenn wir zwei Potenzen mit einer gleichen Basis multiplizieren wollen, dann können wir die Exponenten addieren:
- Wenn wir zwei Potenzen mit einer gleichen Basis dividieren wollen, dann können wir die Exponenten subtrahieren:
Potenzen mit gleichem Exponenten multiplizieren und dividieren
- Wenn wir zwei Potenzen mit einem gleichen Exponent multiplizieren, können wir diese folgendermaßen zusammenfassen:
- Wenn wir zwei Potenzen mit einem gleichen Exponent dividieren, können wir diese so vereinfachen:
Potenzen addieren und subtrahieren
Das Addieren und Subtrahieren von Potenzen ist nur dann möglich, wenn die Potenzen die gleiche Basis und den gleichen Exponenten haben.
Natürlich können wir, wenn die Potenzen keine Variablen enthalten, die Klammern auflösen und addieren/subtrahieren.
Bei gleicher Basis und einer Unbekannten lässt sich höchstens eine Potenz ausklammern:
Sind Exponent und Basis gleich, können die Potenzen addiert oder subtrahiert werden:
Negative Potenzen
Negative Basis
Potenzen mit einer negativen Basis sind negativ, wenn der Exponent ungerade ist und positiv, wenn der Exponent einer geraden Zahl entspricht:
wenn der Exponent gerade ist:
→ Basis positiv
wenn der Exponent ungerade ist:
→ Basis bleibt negativ
Negativer Exponent
Bei einem negativen Exponenten können wir die Potenz so umschreiben:
denn und bildet das Pendant zu
Potenzgesetze für Brüche im Exponenten
Steht im Exponent ein Bruch, können wir diesen in eine Wurzel umschreiben:
Potenzgesetze Aufgaben – Rechnen mit Potenzen

Und jetzt wird trainiert, denn Übung macht den Meister!
Übungaufgaben
Potenzrechnung FAQ
Was ist eine Potenz?
Mithilfe von Potenzen wird ausgedrückt, dass eine Zahl mehrere Male mit sich selbst multipliziert wird. Der Potenzwert ergibt sich aus einer Basis, die mit einem Exponenten hoch genommen wird.
Wie dividiert man Potenzen?
Man kann Potenzen mit gleicher Basis oder mit gleichem Exponenten dividieren. Bei gleicher Basis, werden die Exponenten subtrahiert und die Basis wird beibehalten. Beim gleichen Exponenten werden die Basen dividiert und man behält die Exponenten bei.
Wie multipliziert man Potenzen?
Man kann Potenzen mit gleicher Basis oder mit gleichem Exponenten multiplizieren. Bei gleicher Basis, werden die Exponenten addiert und die Basis wird beibehalten. Beim gleichen Exponenten lässt sich der Exponent ausklammern.
Wir hoffen, dir hat der Artikel geholfen und du kannst nun sicher mit Potenzen rechnen. Wenn du noch mehr Übungsaufgaben benötigst, schau dir mal diese Übungen an.
Wenn du noch konkrete Fragen hast, stell sie uns gerne in den Kommentaren! 🙂
Vielleicht sind ja auch unsere anderen Mathethemen etwas für dich. Schau dich gerne mal auf unserer Seite um. Wir haben alles von schriftlichen multiplizieren bis hin zu absoluten und relativen Häufigkeiten.
Hast du es vielleicht allgemein nicht so mit den Zahlen? Dann wäre Mathe Nachhilfe sehr wahrscheinlich genau das Richtige für dich.
Hier kannst du ganz einfach mit der Mathe Nachhilfe oder der Online Mathe Nachhilfe anfangen.
Wenn du dich vorher noch mehr über das Thema informieren möchtest, findest du hier alle Infos zu unseren Nachhilfe-Leistungen.

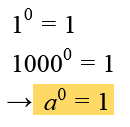
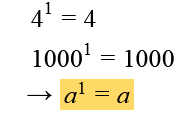
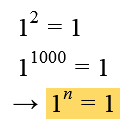
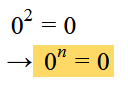
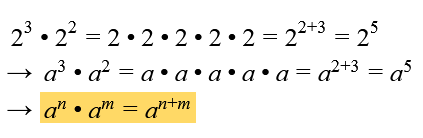
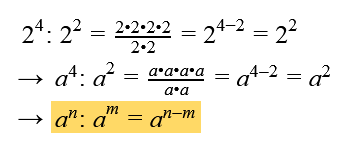
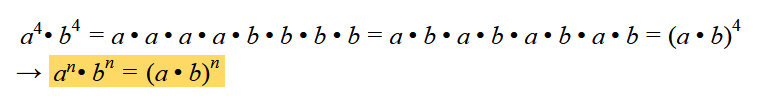
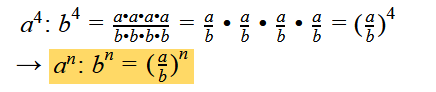
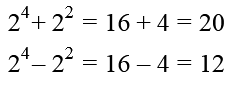
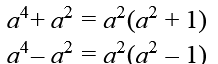
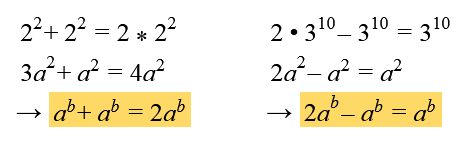
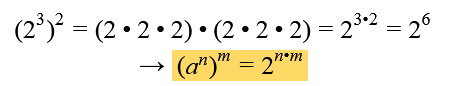
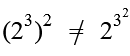 , denn bei Letzteren wird nur der Exponent hoch zwei genommen.
, denn bei Letzteren wird nur der Exponent hoch zwei genommen.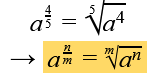
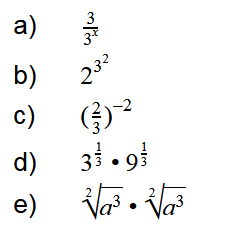
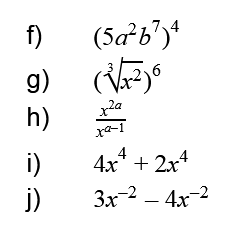


Wann lassen sich Summen von Potenzen nicht zusammenfassen?
1. Potenzen mit unterschiedlichen Exponenten
4³+4² →NICHT MÖGLICH
2. Potenzen mit unterschiedlichen Basen
5²+3² →NICHT MÖGLICH
3. Potenzen mit unterschiedlichen Exponenten und unterschiedlichen Basen
3²+9³ →NICHT MÖGLICH
Wie multipliziert man Potenzen, welche die gleiche Basis und den gleichen Exponenten haben?