5,00 von 5 Sterne
Loading...
Das Pascalsche Dreieck ist ein wichtiges Konzept, das einem in vielen Bereichen der Mathematik begegnet. So tief müssen wir aber gar nicht in die Materie rein, schauen wir uns erstmal in Ruhe die Grundlagen an. Danach bist du schon mal optimal für die nächste Prüfung vorbereitet.
Lass uns keine Zeit und Nerven verlieren. Fangen wir direkt mal an!
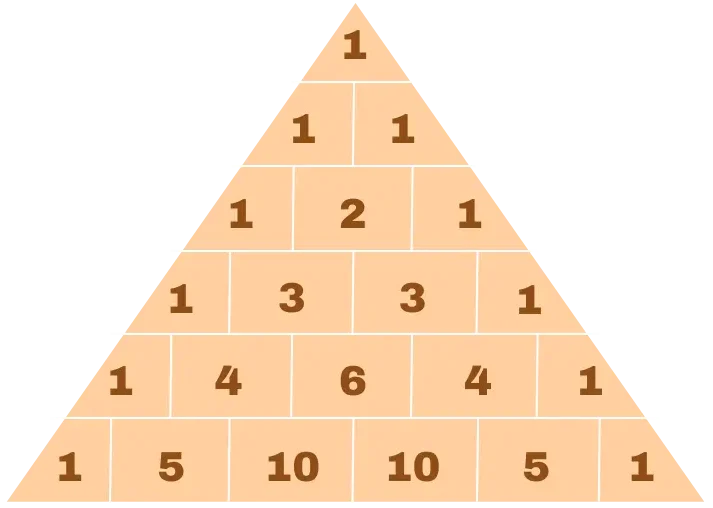
Der Name verrät und zumindest schon mal die Form. Das Dreieck von Pascal ist allerdings besonders, da es aus Zahlen aufgebaut ist. Dabei beginnt man oben mit der Zahl 1. Jede Zahl in diesem Dreieck ist dann die Summe der beiden Zahlen darüber. Das kann man unendlich fortführen.
Aus dem Pascalschen Dreieck kann man dann die binomischen Formeln ableiten oder Binomialkoeffizienten bestimmten – dazu aber später mehr!
Aufbau des Pascalschen Dreieck – Schritt für Schritt erklärt
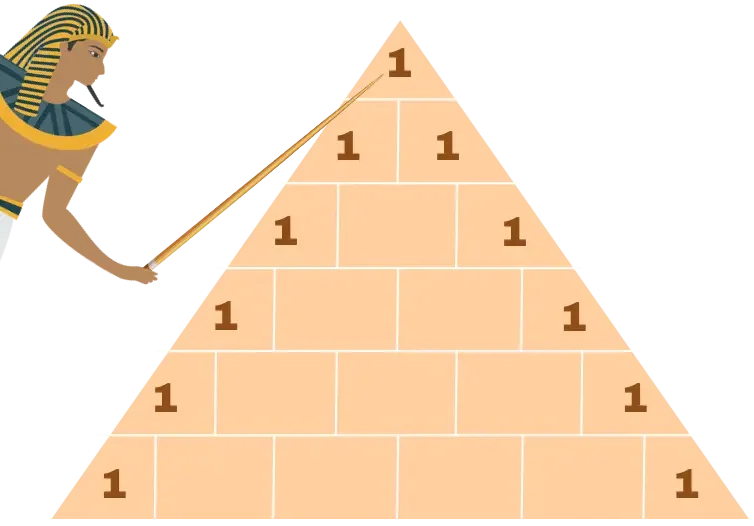
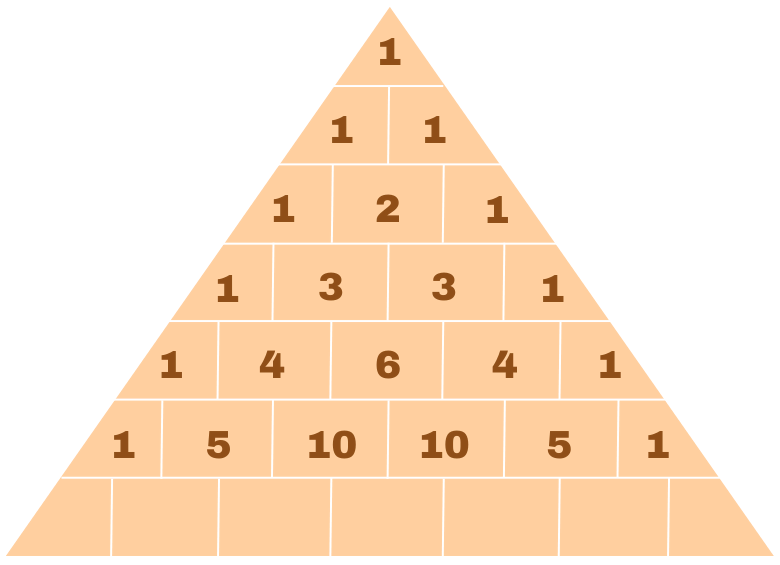
Um das Pascalsche Dreieck aufzubauen, fangen wir ganz oben mit der 1 an. Anschließend wird das Dreieck von oben nach unten weiter befüllt. Es ist dabei wie eine Pyramide aufgebaut, sodass in jeder Ebene eine weitere Zahl pro Reihe dazu kommt und das Dreieck immer breiter wird.
Die Zahlen ergeben sich dabei aus der Addition der beiden Zahlen darüber. In der zweiten Ebene werden daher ebenfalls nur Einsen eingetragen. Die Zahlen am Rand sind dabei ebenfalls immer eine 1.
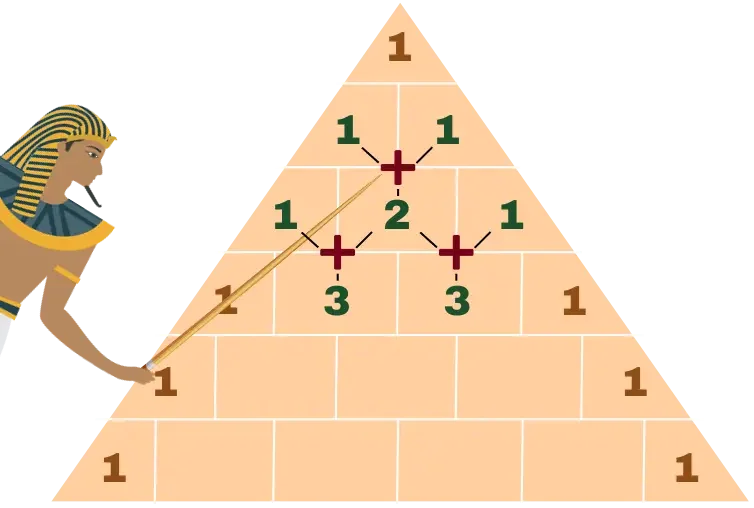
Danach schauen wir uns die dritte Reihe an. Auch hier sind die beiden äußeren Zahlen wieder eine 1. Die mittlere Zahl ist hier die Summe aus den beiden Zahlen darüber. Wir rechnen also 1 + 1 und kommen auf die fehlende Zahl in der Mitte. Das gleiche können wir dann auch direkt für die 4. Zeile machen.
Außen tragen wir die 1 ein und in der Mitte addieren wir.
Das Spiel können wir dann solange spielen wie wir wollen. Das Pascalsche Dreieck ist nämlich durch beliebig viele Zeilen erweiterbar. Die Grundregeln bleiben dabei gleich: Die beiden äußeren Zahlen sind immer eine 1. In der Mitte werden die Zahlen addiert und die Summe darunter geschrieben.
Warum heißt das Pascalsche Dreieck überhaupt so?
- es wurde nach Blaise Pascal (1623-1662) benannt
- war ein französischer Mathematiker, Physiker, Erfinder und Schriftsteller des 17. Jahrhunderts
- Man kommt auch in der Physik nicht an ihm vorbei. So wurde die Einheit des Drucks nach ihm benannt
- entwickelte zudem eine Rechenmaschine, die ein Vorreiter der heutigen Taschenrechner ist.
- er wurde nur 39 Jahre alt, hat aber dafür in vielen wissenschaftlichen Disziplinen einen großen Beitrag geleistet
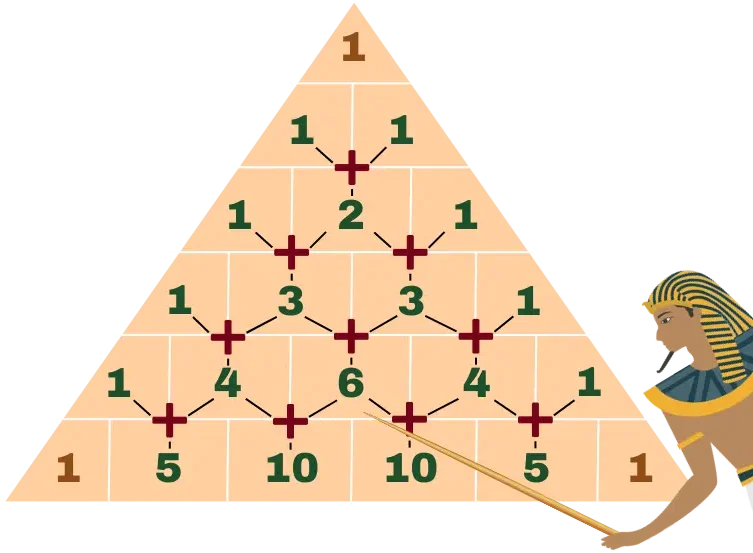
Pascalsches Dreieck Binomische Formel – wo ist der Zusammenhang?
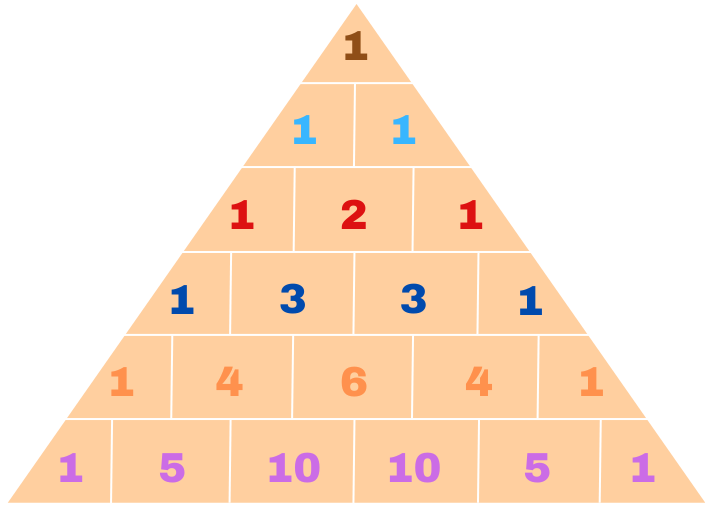
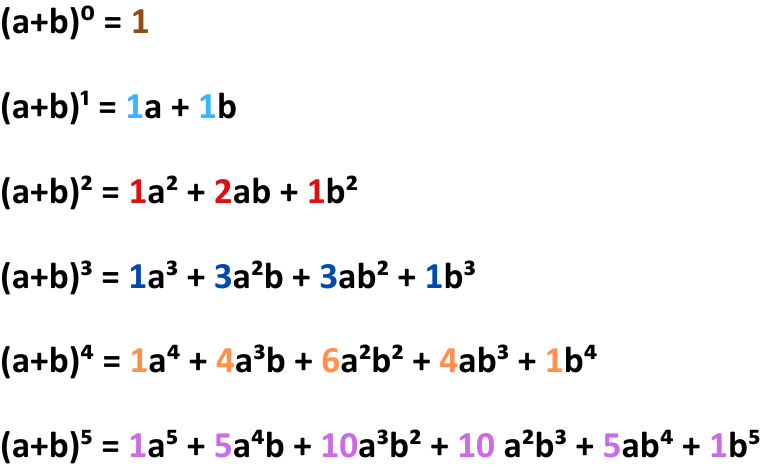
Vielleicht ist es dir selbst schon aufgefallen: Wenn man sich die Zahlen des Pascalschen Dreieck genauer anschaut, kann man Teile der binomischen Formeln darin erkennen.
Uns kann das dann beim Ausmultiplizieren von Klammern helfen. Für jedes Binom kann man die Koeffizienten der Formel nämlich ganz easy aus dem Pascalschen Dreieck ablesen.
Falls du dir also mal nicht sicher bist, wie es mit den Binomischen Formeln weitergeht, hilft dir ein Blick auf das Pascalsche Dreieck. Die Zahlen sind dabei die gleichen, die auch in den binomischen Formeln vor den Variablen stehen.
Pascalsches Dreieck Binomialkoeffizient – einfacher als es sich anhört!
Der Binomialkoeffizient gibt an, auf viele Arten k Elemente aus einer Menge von n Elementen ausgewählt werden können. Die Reihenfolge wird dabei nicht berücksichtigt. Geschrieben sieht das so aus:
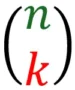
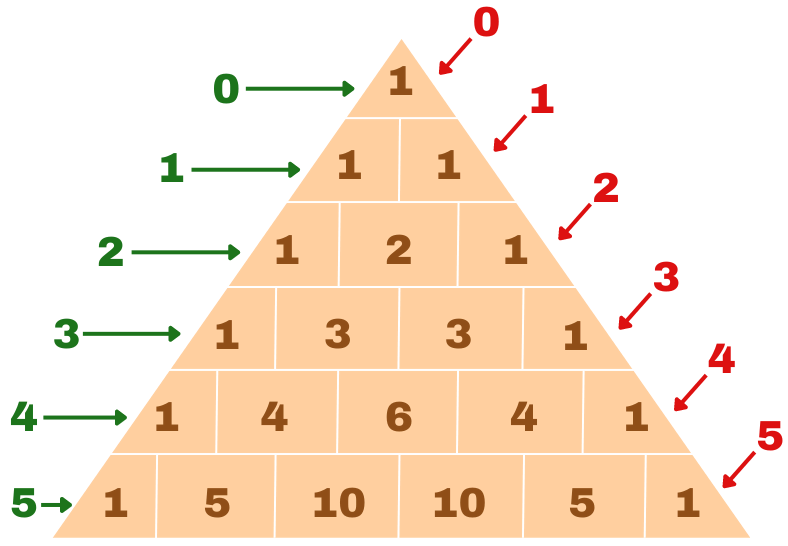
Um unser Pascalsches Dreieck dafür zu benutzen müssen wir vorher noch unsere Reihen und Spalten nummerieren, damit wir die richtige Lösung später nur noch ablesen müssen. Schauen wir uns das ganze am besten Mal an einem Beispiel an. Gesucht ist der Binomialkoeffizient: 
n = 4 und k = 3 – Für uns heißt das, dass wir unseren Binomialkoeffizienten da finden, wo sich die 4. Reihe unseres Pascal’schen Dreiecks mit der 3. Spalte trifft → Wir finden die Zahl 4. Der Binomialkoeffizient im Pascalschen Dreieck gibt dabei an, auf wie vielen Wegen wir bis zum gesuchten Feld kommen können.
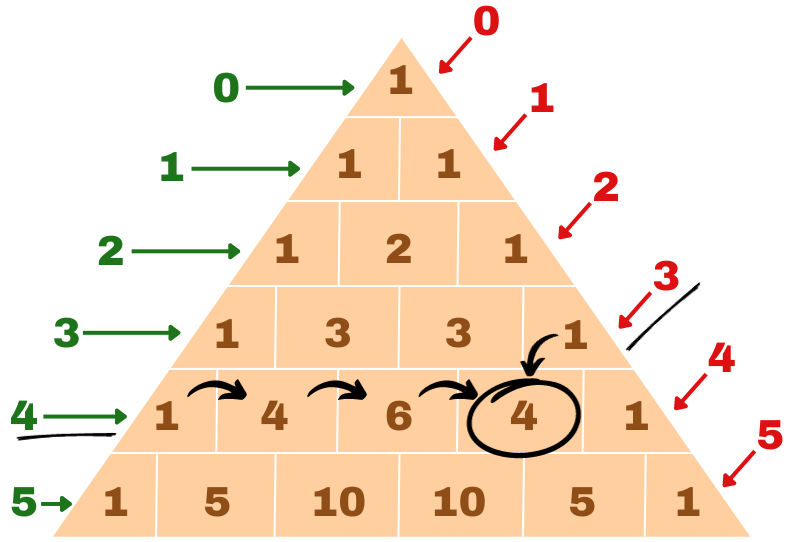
Wir fangen dabei oben bei der 1 an und gehen in jedem Schritt abwärts.
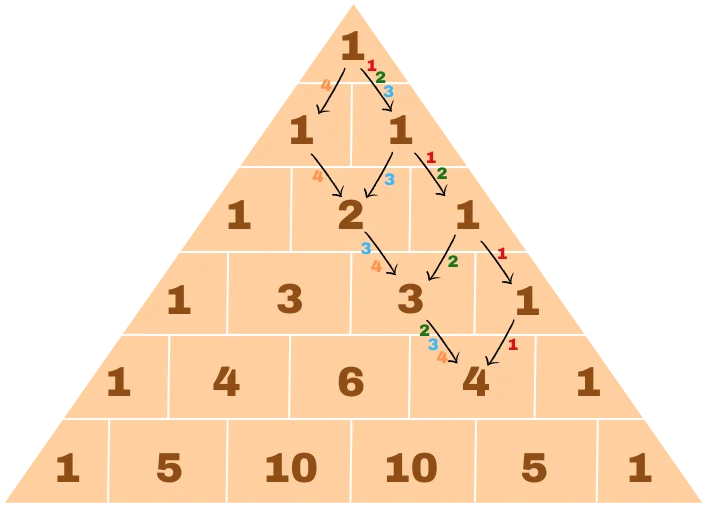
1. Weg: 1 → 1 → 1 → 4
2.Weg : 1 → 1 → 3 → 4
3.Weg: 1 → 2 → 3 → 4
4.Weg: 1 → 2 → 3 → 4
Verstanden? Teste dein Wissen!
FAQ
Was sagt das Pascalsche Dreieck aus?
Das Pascalsche Dreieck ist eine Zahlenpyramide, in der sich die Zahlen immer aus der Summe der direkt darüber liegenden Zahlen ergeben. Das Pascalsche Dreieck hat viele Anwendungsmöglichkeiten und hilft beispielsweise beim Aufstellen binomischer Formeln oder dem Bestimmen von Binomialkoeffizienten.
Wie liest man das Pascalsche Dreieck?
Man beginnt oben bei der 1. Die nächste Reihe ergibt sich dann durch das Addieren der Zahlen darüber. In diesem Fall sind es ebenfalls 1. Danach führen wir das Muster fort.
Dieses mal ergibt sich aus der Addition der beiden Einsen eine 2, die mittig darunter platziert wird. Die beiden Zahlen außen sind erneut eine 1. Das Prinzip kann unendlich fortgeführt werden.
Ist das Pascalsche Dreieck symmetrisch?
Ja! Das Pascalsche Dreieck ist komplett symmetrisch. Die Zahlen in jeder Reihe nehmen zur Mitte hinzu und dann ab der Mitte wieder mit den gleichen Zahlen ab. An beiden Rändern steht immer eine 1.
Wer hat das Pascalsche Dreieck erfunden?
Das Pascalsche Dreieck geht auf den französischen Mathematiker, Physiker, Erfinder und Schriftsteller Blaise Pascal zurück, der dies erstmals in seinem Buch „Traité du triangle arithmétique“ vorstellte.
Wir haben viel Mühe in diesen Artikel gesteckt und freuen uns riesig, wenn du uns eine Sternebewertung oder einen Kommentar hinterlässt. Vielen Dank!
5,00 von 5 SterneLoading...
