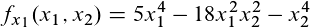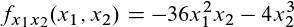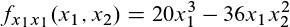3,89 von 5 Sterne
Loading...
Partielle Ableitung ist am Anfang ein etwas unübersichtliches und verwirrendes Thema. Aber mach dir nichts draus! Mit diesem Artikel werde ich dir alles erklären, was du wissen musst. Du erfährst hier…
… erstmal, was die partielle Ableitung überhaupt ist und
… die Berechnung erster und zweiter Ordnung an einem Beispiel
Lass uns gleich mal anfangen!
Die partielle Ableitung ist Bestandteil der Differentialrechnung (Analysis). Sie wird verwendet, um eine Funktion mit mehreren Variablen nach genau einer aufzulösen. Man sucht sich also eine der Variablen aus und leitet nach dieser ab (die übrig gebliebenen werden konstant gehalten).
Dementsprechend ist es wichtig, dass du die Ableitung im Allgemeinen bereits beherrschst. Aber keine Sorge:
Wir haben extra Artikel zu den Differentiationsregeln (also Ableitungsregeln) erstellt, die dir das Thema zur Not nochmal erklären können. Schau mal vorbei, wenn du noch Hilfe brauchen solltest.
Also mach dir nichts draus, wir schaffen das schon zusammen!
Noch zur Info für dich:
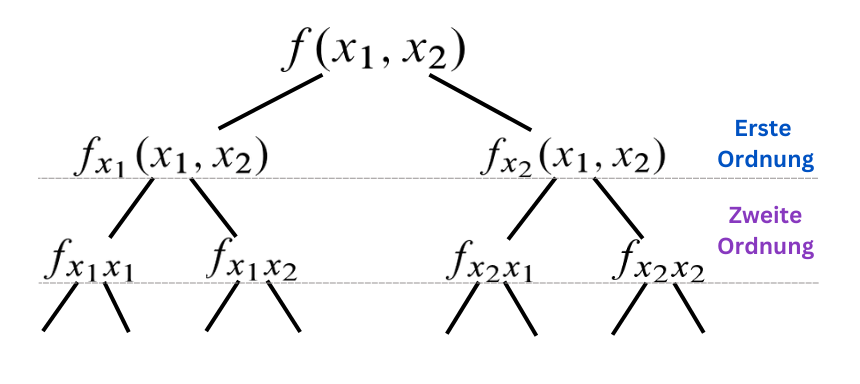
Wie du später im Beispiel sehen wirst, sind die partiellen Ableitungen zweiter Ordnung etwas “unübersichtlich”, weshalb wir höhere Ordnungen hier nicht durchgehen werden.
Ich habe dir hier mal eine Übersicht aufgestellt: je höher die Ordnung geht, desto komplexer wird das Ganze auch.
Allerdings ändert sich das Verfahren zum Berechnen nicht. Wenn du also die ersten beiden Ordnungen berechnen kannst, schaffst du auch die höheren!
Berechnung Schritt-für-Schritt
Die Berechnung schauen wir uns mal zusammen an einem Beispiel an.
Ableitung erster Ordnung
Beginnen wir mal mit der partiellen Ableitung erster Ordnung. Wir schauen uns die Ausgangsfunktion an und legen fest, nach welcher Variable zuerst abgeleitet werden soll.
Lass uns mit x1 starten:
x1 ist unsere Variable, nach der wir nun ableiten wollen (sie wird als Index unten an die Funktion angeschrieben)
x2 ist somit unsere Konstante.
Wie geht es nun mit der Berechnung weiter?
x1 ist unsere Variable und x2 die Konstante (danach wird nicht abgeleitet).
Tipp
Am Besten ist es für dich, wenn du in der Gleichung “Bestandteile” mit Bleistift markierst (was gehört zur Variable / was zur Konstante?). So kannst du sichergehen, dass du bspw. keine Vorzeichen vergisst, die Konstante ableitest oder Faktoren übersiehst.
Hier einmal die Ausgangsgleichung, mit der wir im Beispiel arbeiten werden.
Wir leiten x1 nun nach den üblichen Regeln ab. Denk daran, dass Faktoren mit x2 mitgenommen und nicht abgeleitet werden. Nur das x1 wird hier betrachtet!
Am Ende kommt dann folgende Funktion raus:
Jetzt fassen wir das Ganze einmal zusammen und haben folgendes Endergebnis:
Zur Übung für dich: versuche mal die Ableitung erster Ordnung mit der Variable x2 (x1 ist also die Konstante) zu berechnen. Schnapp dir Zettel und Stift und los geht es!
Ausgangsgleichung
Die Lösung findest du hier zum Ausklappen:
Lösung - Ableitung erster Ordnung nach x2
- markiere die Bestandteile in der Ausgangsgleichung
- lege x2 als Variable fest, nach der du Ableiten willst
- leite alle Bestandteile mit x2 normal ab (achte auf die Konstante x1!)
Lösung:
Falls du einen Fehler gemacht hast, nochmal eine kurze Erklärung:
Ausgangsgleichung:
Wenn du die Bestandteile markiert hast, wirst du sehen, dass das Erste x1 weg fällt beim Ableiten. Die anderen Faktoren mit x1 bleiben erhalten und werden nicht mit abgeleitet. Alle Bestandteile mit x2 werden auf normalem Weg abgeleitet.
Hervorragend! Damit hast du die partielle Ableitung erster Ordnung abgeschlossen!
Jetzt geht es weiter mit der zweiten Ordnung.
Ableitung zweiter Ordnung
Hierfür schauen wir uns NUR die Ableitungen erster Ordnung an (die Ausgangsfunktion ist hier nicht mehr wichtig).
Ich zeige dir die beiden Funktionen, mit denen wir jetzt arbeiten (Lösungen vom Abschnitt vorher):
Wie geht es hier jetzt weiter?
Im Grunde genommen, bleibt die Schrittfolge gleich, wie bei der Ableitung erster Ordnung. Das heißt:
- lege fest, nach welcher Variable du ableiten willst
- markiere die Bestandteile, damit du nichts vergisst
- leite nach der ersten Variable ab (die Konstante bleibt unverändert oder fällt weg)
Ich habe im Beispiel wieder mit x1 als Variable und x2 als Konstante angefangen, damit du den Unterschied besser erkennst.
Dies wird folgendermaßen geschrieben:
Der erste Index (x1) zeigt, in welcher Funktion wir uns befinden. Hier bedeutet das also, dass wir uns die partielle Ableitung erster Ordnung von x1 anschauen. Der zweite Index (x2) sagt, dass wir bei der festgelegten Funktion nach x2 ableiten wollen.
Nehmen wir also die folgende Gleichung als Ausgangspunkt:
Jetzt geht es weiter mit dem Ableiten. Der erste Bestandteil fällt weg, weil das x1 mit einem Minuszeichen an den Rest angebunden ist. Alles andere wird normal abgeleitet.
Das Ergebnis sieht dann so aus:
Fassen wir das Ganze zusammen, würde die Gleichung lauten:
Das war doch gar nicht so schwer, oder? Jetzt wirst du wahrscheinlich auch schon merken, wie hilfreich das Markieren der Bestandteile ist. Hier kann man sich gerne mal versehen.
Aber, wir sind ja noch nicht fertig!
Jetzt kommen die Ableitungen zweiter Ordnung für den Rest. Wir machen die letzte Ableitung zu x1 noch zusammen und dann lass ich dich wieder selbst rechnen.
Nach x2 haben wir ja bereits abgeleitet, also fehlt uns nur noch x1.
Merke dir: 1. Index ist die Funktion in der wir uns befinden. Der 2.Index sagt, nach welcher Variable wir ableiten (hier ist jetzt beides x1)
Wenn wir die Funktion nun nach x1 ableiten, kommt folgendes Ergebnis raus:
Und dann noch einmal zusammenfassen:
Damit haben wir die partielle Ableitung zweiter Ordnung für die Funktion x1 abgeschlossen.
Jetzt fehlt uns aber noch eine Funktion. Ich möchte, dass du dir hier wieder Zettel und Stift in die Hand nimmst. Versuche jetzt mal, die letzten beiden Ableitungen durchzuführen.
Die Lösung ist hier zum Ausklappen bereit!
Lösung - Ableitung zweiter Ordnung
Gleichung, mit der wir arbeiten:
Merke dir: 1.Index = Gleichung, in der wir uns befinden. 2.Index = nach dieser Variable leiten wir ab.
Ableitung zweiter Ordnung nach x1
Berechnung:
Endergebnis:
Ableitung zweiter Ordnung nach x2
und zusammengefasst:
Perfekt! Das ist es schon gewesen!
Wie du siehst ist es am Anfang etwas kompliziert, aber wenn man es einmal verstanden hat, dann ist es kein Problem mehr.
Deshalb: gehe die Schrittfolgen immer wieder durch und lerne das Ableiten!
Zusammenfassung Beispiel (Übersicht)
Ich habe dir hier zum Abschluss unser berechnetes Beispiel als Übersicht mitgebracht. Du kannst es dir auch gerne herunterladen und in Ruhe dann nochmal anschauen.
Wenn du die einzelnen Schritte nochmal durchgehen möchtest, habe ich dir hier unten nochmal alles mit aufgeschrieben.
Partielle Ableitung erster Ordnung
Partielle Ableitung erster Ordnung
Ausgangsgleichung
Partielle Ableitung erster Ordnung nach x1:
Partielle Ableitung erster Ordnung nach x2:
Im nächsten Abschnitt kommen dann die partiellen Ableitungen zweiter Ordnung.
Partielle Ableitung zweiter Ordnung
Partielle Ableitung zweiter Ordnung
Ausgangsgleichung – Ableitung erster Ordnung nach x1
Partielle Ableitung zweiter Ordnung nach x1
Partielle Ableitung zweiter Ordnung nach x2
Ausgangsgleichung – Ableitung erster Ordnung nach x2
Partielle Ableitung zweiter Ordnung nach x1
Partielle Ableitung zweiter Ordnung nach x2
Zusammenfassung zu partiellen Ableitungen
Zusammenfassend kann also gesagt werden, dass die partiellen Ableitungen am Anfang etwas verwirrend sein können. Aber das Verfahren ist recht simpel und – da du dich mit der Ableitung schon auskennst – kommt nicht wirklich was Neues dazu, was du dir merken musst.
Du hast in diesem Artikel gelernt, wozu partielle Ableitungen gebraucht werden und wie man die Ableitung erster und zweiter Ordnung berechnet. Wie am Anfang schon einmal gesagt: die Ableitungen höherer Ordnungen werden nach dem gleichen Verfahren berechnet – also steht dir dort nichts mehr im Weg!
Dementsprechend: lerne die Schrittfolge und Ableitungsregeln und dann sollte nichts mehr schief gehen!
Hat dir der Artikel geholfen?
Wir haben uns sehr viel Mühe gegeben, diesen Artikel für dich zu erstellen. Bitte lass einen Kommentar oder eine Bewertung für uns da, ob und wie der Artikel dir weiter helfen konnte. Dankee!
3,89 von 5 SterneLoading...
