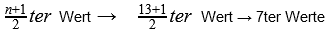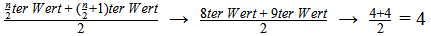Median berechnen – einfach erklärt (+Übungsaufgaben)

Statistik ist eins der schwierigsten und gefürchtetsten Themengebiete für Schüler und Studenten. Aber keine Sorge! Wir zeigen dir, dass du keine Angst davor haben musst, den Median zu berechnen.

Schritt für Schritt führen wir dich zur Formel, damit du am Ende genau weißt, wie du diese verwendest.

Median – Definition

Der Median (auch Zentralwert genannt) gehört wie der Modalwert und das arithmetisches Mittel zu den Maßen der zentralen Tendenz (Lagemaße) aus der deskriptiven Statistik. Mithilfe de genannten Kennwerte lässt sich eine Maßzahl für die Mitte einer Wertereihe finden.

Die deskriptive Statistik hat das Ziel empirische Daten zu beschreiben und übersichtlich darzustellen. So können große Datenmengen vereinfacht zusammengefasst werden.

Um den Median zu bestimmen, benötigen wir also eine Wertereihe, die mindestens eine Ordinalskalierung aufweist. Wenn man den Median bestimmt hat, kann man folgende Aussage treffen:

50% aller Werte in der Datenreihe liegen unter dem Median und die anderen 50% der Werte liegen darüber.

Haben wir eine Liste der Noten von der letzten Klassenarbeit, können wir den Median dieser Wertereihe bestimmen. Ist der Median 4, stellen wir fest, dass ca. 50% der Klasse eine bessere Note als eine 4 hat und 50% eine schlechtere Note.

Der Modalwert, das arithmetische Mittel und der Medianwert sind Lagemaße, um die typische Tendenz einer Wertereihe zu beschreiben.

Dabei unterscheiden sich alle drei in der mathematischen Berechnung, sodass ein unterschiedliches Skalenniveau Voraussetzung ist. Falls du nicht mehr genau weißt, wie man das Skalenniveau bestimmt, schau mal bei unserem Beitrag über das Skalenniveu vorbei.

Medianwert (Median) – kurz erklärt

• Voraussetzung: Ordinalskalierung→ Rangordnung möglich, aber keine gleichen Abstände der Ränge zueinander
• Wert, der die Wertereihe in zwei Hälften teilt
• resistent gegenüber Ausreißern, kann aber einen Wert annehmen, den es in der Verteilung gar nicht gibt

Modalwert (Modus) – kurz erklärt

• Voraussetzung: Nominalskalierung
• Wert, der in einem Datensatz am häufigsten vorkommt, also mit höchster absoluter und relativer Häufigkeit
• gibt nur Höhepunkte an, bei bimodalen/multimodalen Verteilungen allerdings oft sinnvoller als der Median und das arithmetische Mittel

Arithmetisches Mittel – kurz erklärt

• Voraussetzung: Intervallskalierung
• Wert, der sich beim gleichmäßigen Aufteilen der Summe aller Daten auf die Erhebungseinheiten ergibt
• jeder Wert geht in die Berechnung mit ein, ist aber sensibel für Ausreißer, auch das arithmetische Mittel kann einen Wert annehmen, den es in der Verteilung nicht gibt

Berechnung Median

Um den Median-Wert berechnen zu können, müssen wir unsere Daten zunächst aufsteigend nach der Größe sortieren. Damit du verstehst, wie das gemeint ist, hier ein Beispiel.

Eine Wertereihe besteht aus folgenden 8 Zahlen:

Du kannst diese nun aufsteigend sortieren:

wenn n die Anzahl der Werte darstellt, gilt:

Da der Wert zwischen dem und dem Wert liegt, kommst du so auf den Mittelwert der beiden. In diesem Fall nimmt der Median einen Wert an, den es so in der Verteilung nicht gibt.

Berechnen wir das Beispiel von oben. Dort ist n=8, also gerade. Der Median liegt hier zwischen dem und Wert, also zwischen dem 4ten und 5ten Wert. In der Tabelle sehen wir nun, dass der 4te Wert 2 ist und der 5te Wert 3.

Um den Median (Md) zu erhalten, werden diesen beiden Werte nun addiert und anschließend durch zwei geteilt.

Das bedeutet: Die Hälfte aller Werte liegen unter 2,5 und die andere Hälfte darüber.

Hier ein Beispiel:

In diesem Fall ist n=9 und somit ungerade. Wir rechnen mit der Formel:

Auf dem 5ten Wert in unserer Tabelle findest du den Median.
Md= 3
Die Hälfte aller Werte liegt also unter 3 und die andere Hälfte über 3.

Median bestimmen – Übungsaufgaben

Median Statistik – FAQ