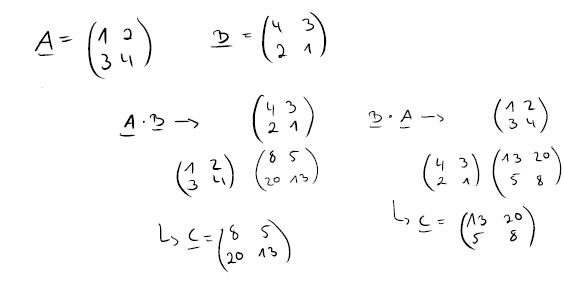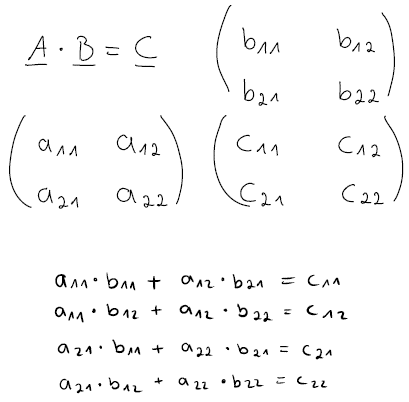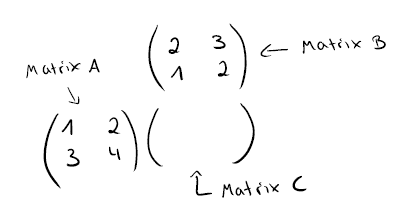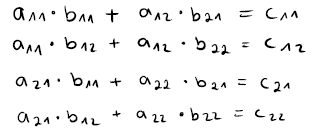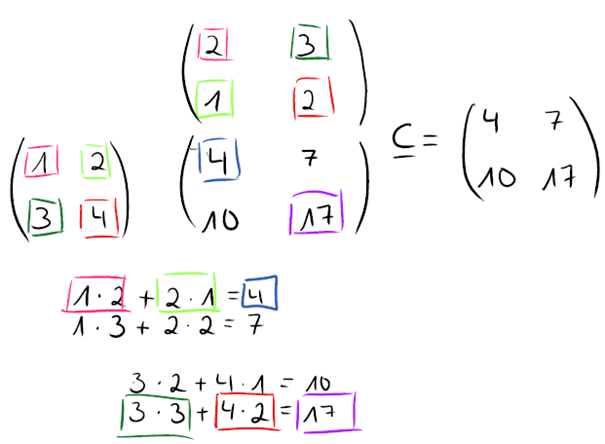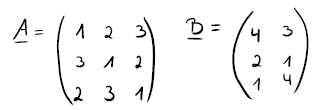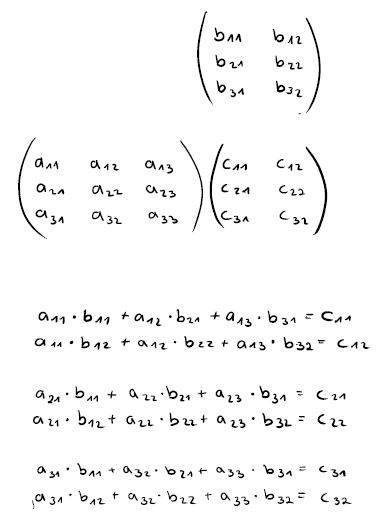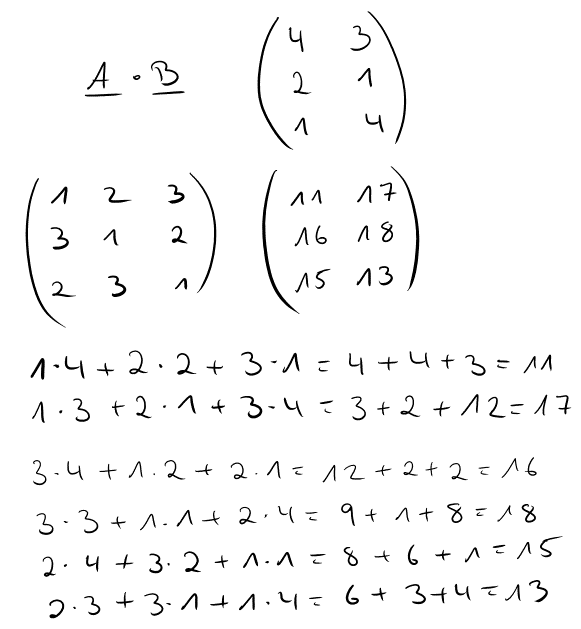3,50 von 5 Sterne
Loading...
Matrizen zu multiplizieren ist am Anfang etwas verwirrend, aber wenn du es einmal verstanden hast, ist es super einfach!
In diesem Artikel werde ich dir zeigen…
… welche Gesetze beim Multiplizieren zu beachten sind (Übersicht) und
… ein Beispiel anhand des Falk-Schemas (mit 2×2 und 3×3 Matrizen)
Danach wirst du das Thema sicher verstanden haben. Also fangen wir gleich mal an!
Bevor es los geht, noch eine kurze Info für dich:
Wir haben einen Artikel über Matrizen im Allgemeinen erstellt. Da kannst du gerne mal vorbei schauen, wenn du noch Hilfe bei anderen Themen brauchen solltest.
Da du dich ja schon mit Matrizen auskennst, werden wir noch einmal die Schreibweise für diesen Artikel klären:
- Matrix vom Typ (m,n)
- Element: aij → a = Zahl, i = Zeile, j = Spalte
1. Index Zeilennummer (m)
2. Index Spaltennummer (n)
Die Matrixschreibweise würde dann folgendermaßen aussehen:
- Matrix: A
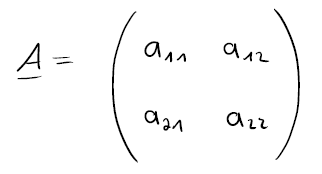
Regeln für die Multiplikation (Übersicht)
Matrizenprodukt: C = A B
→ genauso viele Zeilen, wie linker Faktor A und
→ genauso viele Spalten, wie rechter Faktor B
Ich habe dir hier mal eine grobe Übersicht der Rechenregeln mitgebracht, die grundlegendes für diesen Artikel darstellt.
Du kannst dir diese Übersicht gerne herunterladen, falls du sie brauchen solltest.
Die Regeln gehen natürlich noch weiter – wenn wir an transponierte Matrizen denken o.ä. – aber für diesen Artikel reicht das vollkommen aus.
Was passiert, wenn du Faktoren vertauschst?
Das Kommutativgesetz gilt nicht bei der Multiplikation von Matrizen! Das heißt, dass die Position der Faktoren nicht vertauscht werden darf, da sich das Endergebnis sonst ändert.
Wenn du dir das anhand eines Beispiels mal anschauen möchtest, dann gibt es das hier einmal zum Ausklappen.
Wieso kein Kommutativgesetz?
Wie du an der Matrix C erkennen kannst, kommt bei beiden Rechnungen etwas vollkommen anderes heraus.
Vertauschst du also die Positionen der Matrizen, ist das Endergebnis nicht gleich! Behalte das also immer im Hinterkopf, wenn du eine Multiplikation mit Matrizen durchführst.
Beispiele zur Berechnung (Falk-Schema)
Kommen wir nun endlich zu der eigentlichen Berechnung. Wir werden in diesem Abschnitt Matrizen miteinander multiplizieren, mithilfe des Falk-Schemas.
Für das Falk-Schema habe ich dir mal eine kleine Übersicht mitgebracht, wie das Ganze aussieht:
In der Übersicht wird Matrix A mit Matrix B multipliziert. Das Ergebnis ist die Matrix C.
Die Berechnung mit dem Falk-Schema verläuft immer nach diesem Prinzip.
Matrizen mit Matrizen multiplizieren
Jetzt geht es mit der Berechnung weiter.
Wenn du das Thema zum ersten Mal behandelst, dann schau dir die 2×2 Matrizen an (das ist erstmal einfacher zu verstehen).
Ansonsten kannst du gleich auch schon zu den 3×3 Matrizen weiter gehen. Das Verfahren ändert sich nicht, es kommen nur mehr Zahlen dazu.
Um erstmal in das Thema reinkommen zu können, beginnen wir mit den 2×2 Matrizen.
Es sind folgende Matrizen gegeben:
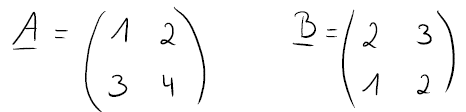
Die Rechnung lautet: A * B
Zu aller erst, wird der Typ der Matrizen verglichen, ob man die beiden auch multiplizieren kann:
- Matrix A, vom Typ (2,2)
- Matrix B, vom Typ (2,2)
Jetzt geht es weiter mit der Erstellung des Falk-Schemas.
Wie du sehen kannst: die Matrix A (auf der linken Seite in der Formel), wird links angeschrieben. Matrix B (auf der rechten Seite der Formel) wird oben angeschrieben. Der Treffpunkt beider Matrizen stellt dann die Matrix C dar (unser Endergebnis).
Die Berechnung läuft nun folgendermaßen ab:
Wenden wir diese Berechnungsschritte bei dem Falk-Schema an, kommt folgendes raus:
Und schon konnte Matrix C berechnet werden!
Tipp am Rande: die Berechnung stellt eine große Fehlerquelle da, weil man sich gerne mal vertut. Also lass dir Zeit beim Rechnen und schau alles gründlich nach.
Die Berechnung erfolgt hier auf die gleiche Weise, wie bei den 2×2 Matrizen auch schon. Gehe einfach immer die selbe Schrittfolge durch:
- prüfe, ob die Matrizen überhaupt multipliziert werden dürfen (Spalte links MUSS Zeile rechts)
- wenn ja, dann erstelle das Falk-Schema (WICHTIG: achte auf die Reihenfolge der Faktoren!)
- nun folgt die Berechnung, nach dem altbekannten Schema.
Gegeben sind folgende Matrizen:
Können wir die beiden miteinander multiplizieren?
Die Rechnung lautet wieder: A * B
- Matrix A ist vom Typ (3,3), Matrix B vom Typ (3,2).
- Spaltenzahl der linken Matrix stimmt also mit der Zeilenzahl der rechten Matrix überein – wir können sie miteinander multiplizieren.
Jetzt legen wir das Falk-Schema an und tragen die Matrizen an den jeweiligen Stellen ein.
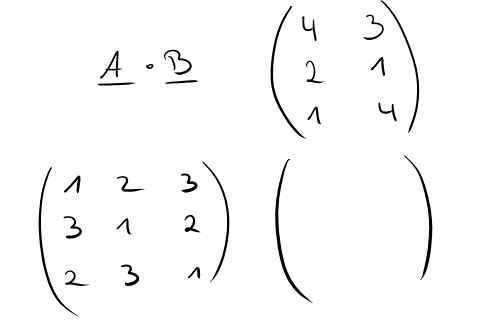
Jetzt folgt wieder die Berechnung der Matrix C nach dem altbekannten Schema.
Der einzige Unterschied: wir haben jetzt mehr Elemente, mit denen wir rechnen müssen. Deshalb sieht die Berechnung im Gesamten letztendlich so aus:
Das Endergebnis würde dann folgendermaßen aussehen:
Wie du siehst, ist das Verfahren an sich recht simpel. Aber, das addieren der richtigen Faktoren stellt eine häufige Fehlerquelle da. Also lass dir beim Berechnen Zeit, damit du nicht durcheinander kommst.
Matrizen multiplizieren – Zusammenfassung
Wir halten also folgendes fest:
Um Matrizen miteinander multiplizieren zu können, muss die Spaltenzahl der linken Matrix mit der Zeilenzahl der rechten Matrix übereinstimmen. Ist das gegeben, kannst du beispielsweise das Falk-Schema anwenden, um das Ergebnis zu berechnen.
Bei der Berechnung vom Falk-Schema kann man schnell mal durcheinander kommen – also lass dir Zeit beim Rechnen und geh alles gründlich durch.
Konnte dir der Artikel helfen?
Wir haben uns viel Mühe bei der Erstellung des Artikels geben. Deshalb würden wir uns umso mehr darüber freuen, wenn du eine Bewertung oder einen Kommentar dalassen könntest. Vielen Dank!
3,50 von 5 SterneLoading...
