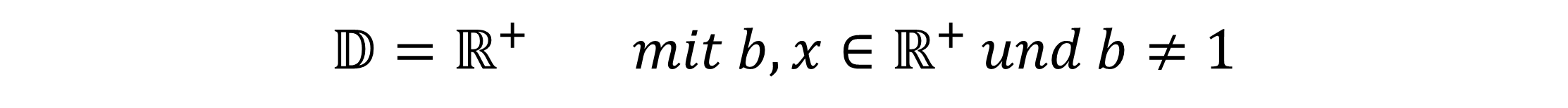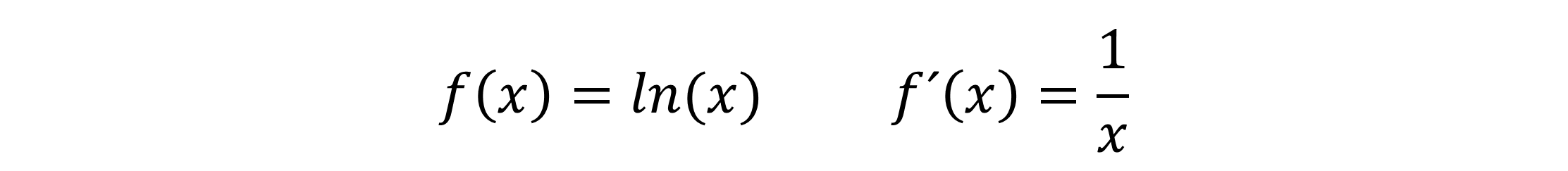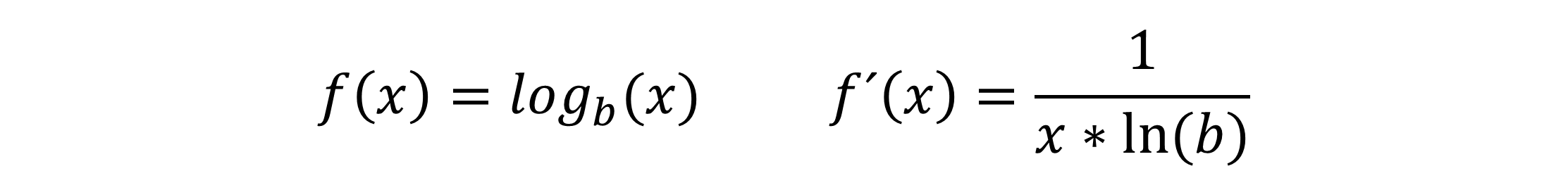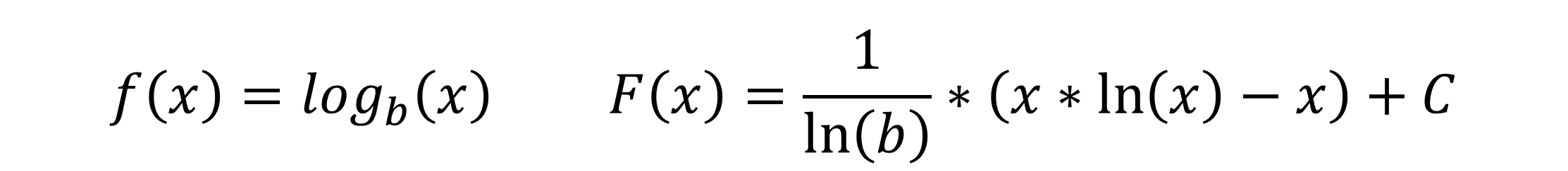Logarithmusfunktion in 5 Minuten erklärt

Du hattest die Logarithmusfunktion im Matheunterricht in der Schule und hast noch Fragen. Dieser Artikel zeigt dir die Eigenschaften, die Formel, sowie die Ableitung, als auch das Integral der Logarithmusfunktion.

Alles wird dir leicht verständlich anhand von Beispielen und Graphen erklärt.

Lasst uns loslegen!

Logarithmusfunktion Formel

Die allgemeine Logarithmusfunktion hat die folgende Funktionsgleichung:

Ausgesprochen wird das als “Logarithmus von x zur Basis b”.

Logarithmusfunktion ableiten

Wir erklären dir jetzt, wie du ganz simpel die allgemeine Logarithmusfunktion, sowie den natürlichen Logarithmus ableiten kannst.

Natürliche Logarithmusfunktion

Der natürliche Logarithmus, auch Logarithmus naturalis genannt, ist eigentlich nichts weiter als der Logarithmus zur Basis e. Die Eulersche Zahl e hat ungefähr den Wert 2,7183. Die Ableitung für diese Funktion kannst du dir recht leicht merken, da sie wie folgt aussieht:

Allgemeiner Logarithmus

Die Ableitung f´(x) für den allgemeinen Logarithmus lautet:

Logarithmusfunktion Integral

Selbstverständlich kannst du die Logarithmusfunktion auch integrieren. Die Stammfunktion der allgemeinen Logarithmusfunktion lautet wie folgt:

Logarithmusfunktion Erklärung

Aber wofür brauchst du überhaupt die Logarithmusfunktion? Um dir das ganze zu erklären, nehmen wir uns mal ein Beispiel. Stell dir vor, du hast die folgende Gleichung 2^y=16 und möchtest herausfinden, was unser y für einen Wert hat.

Um auf die Lösung 4 zu kommen könntest du durch ausprobieren verschiedene Werte für das y einsetzen. Dieser Weg ist gerade bei komplizierten Gleichungen, wie der hier gegebenen, sehr mühsam.

Genau hier kommt uns der Logarithmus zur Hilfe. Wenn du log₂(16) in deinen Taschenrechner eingibst, kommst du direkt auf die Lösung y=4. Der Logarithmus ist also die Antwort auf die Frage, mit welcher Zahl y du b potenzieren musst, um x zu erhalten.

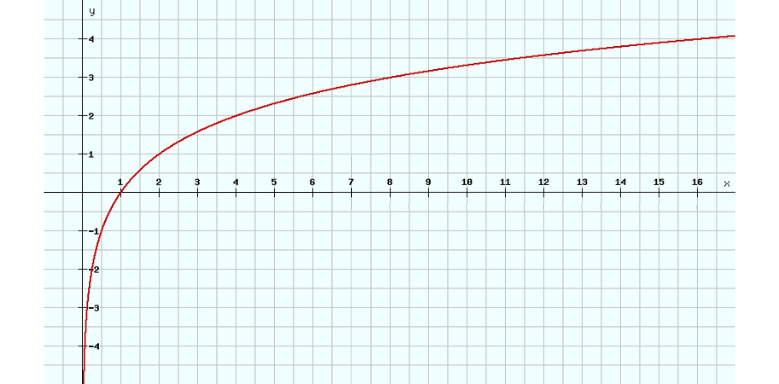
Der Graph der Logarithmusfunktion, auf dem der Punkt aus unserer Beispielfunktion liegt, hat die folgende Funktion f(x)=log₂(x) und sieht wie folgt aus:

Logarithmusfunktion Eigenschaften

Jetzt zeigen wir dir die wichtigsten Eigenschaften der Logarithmusfunktion.

Umkehrfunktion Exponentialfunktion

Wie du bereits im Beispiel aus dem Erklärungs-Abschnitt gesehen hast, löst der Logarithmus die Beispielfunktion. Deshalb ist die Umkehrfunktion der Logarithmusfunktion die Exponentialfunktion:

Sowohl für die Exponentialfunktion als auch die Logarithmusfunktion gilt:

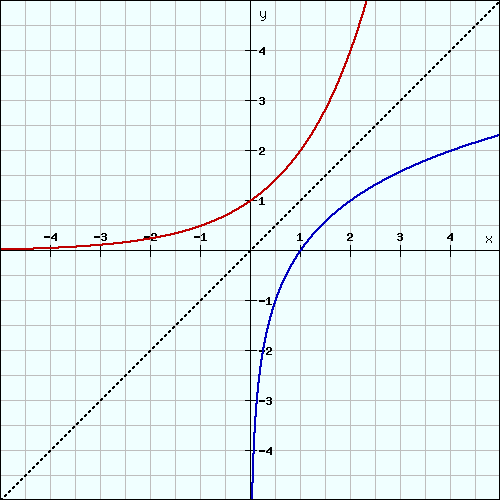
Aufgrund der Eigenschaft, dass die beiden Funktionen Umkehrfunktionen voneinander sind, sind die Graphen von beiden Spiegelbilder an der Geraden y=x.

Am besten zeige ich dir das an einem Beispiel mit der Exponentialfunktion f(x)=2^x (rot) und der Logarithmusfunktion f(x)=log₂(x) (blau):

Monotonie

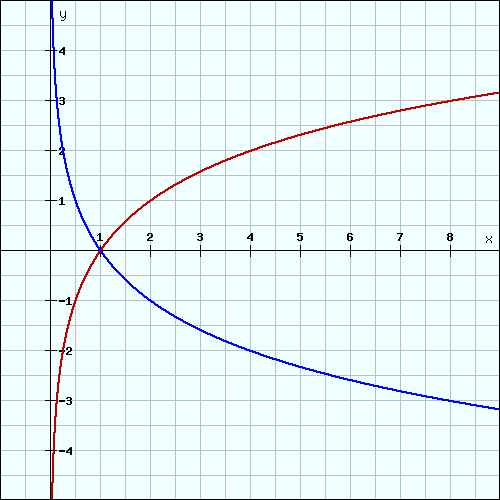
Eine weitere Eigenschaft der Logarithmusfunktion ist, dass diese streng monoton fällt oder steigt, je nachdem, welchen Wertebereich die Basis b hat.

Liegt der Wert von b im Intervall zwischen 0 und 1, dann fällt die Funktion streng monoton. Ist der Wert von b größer als 1, so haben wir eine streng monoton steigende Funktion. In dem Beispielbild haben wir die Funktionen log₂(x) (rot) und log_0,5(x) (blau):

y-Achse = Asymptote

Des Weiteren kannst du an den Graphen erkennen, dass sich eine Logarithmusfunktion für x-Werte nahe 0 der y-Achse annähert, diese jedoch nicht berührt. Deshalb ist die y-Achse die senkrechte Asymptote für die Funktion.

Koordinatenachsen Schnittpunkte

Wie du aus dem vorherigen Abschnitt bereits weißt, berührt der Graph der Logarithmusfunktion nie die y-Achse, weshalb es auch keinen Schnittpunkt mit dieser gibt. Es existiert jedoch ein Schnittpunkt mit der x-Achse.

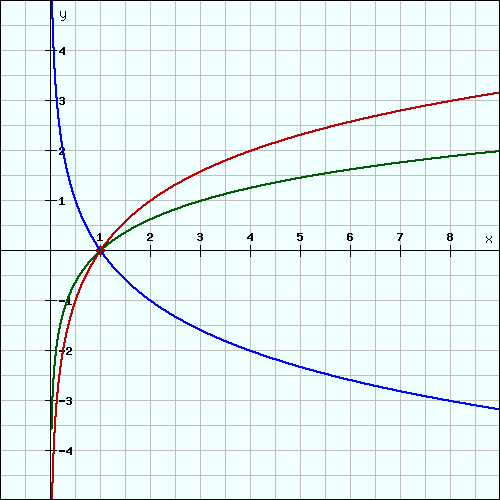
Dieser verläuft IMMER durch den Punkt (1|0), denn egal welchen Wert b hat, b⁰=1. Deshalb ist x=1 die einzige Nullstelle einer Logarithmusfunktion. Damit du das besser verstehst, zeigen wir dir das ganze an Hand von ein paar Graphen:

Logarithmusfunktion Graph zeichnen

Wenn du eine Logarithmusfunktion hast und schnell gucken möchtest wie der Verlauf des Graphen ist, dann nutz doch das Online-Tool, das wir zum erstellen der Graphen genutzt haben.