Du kennst Lineare Gleichungen bzw. Lineare Funktionen aus dem Matheunterricht in deiner Schule, hast aber noch ein paar Verständnisprobleme?
In diesem Artikel erfährst du, was lineare Gleichungen sind und wie du sie nutzen kannst. Alles wird dir leicht verständlich mithilfe von Abbildungen erklärt.
Lass uns direkt loslegen!
Lineare Gleichungen kann man auch Gleichungen ersten Grades nennen, weil die Variable nur in der ersten Potenz vorkommt. Wenn diese Variable x ist, heißt das, dass es keine Teile mit x², x³ und so weiter gibt, sondern nur x.
Lineare Gleichungen Beispiele
f ( x ) = 3 x + 5
g ( x ) = 2 x – 4
Lineare Funktionen Formel
Die allgemeine Formel für lineare Gleichungen lautet:
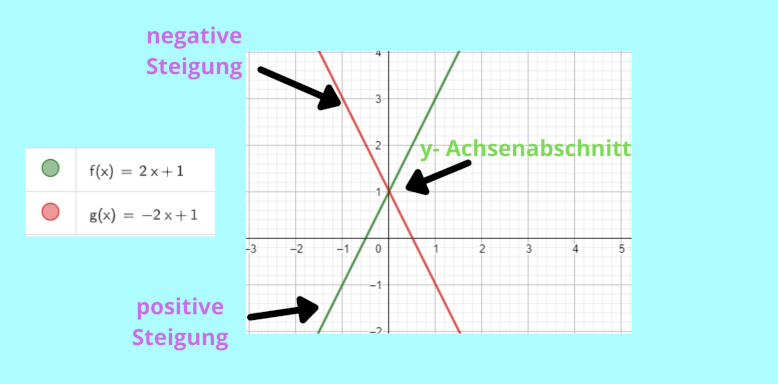
Das b beschreibt den y-Achsenabschnitt. Das ist also der Punkt, an dem die lineare Funktion die y-Achse schneidet.
Die Steigung steht in m. Dadurch wird erklärt, wie flach oder steil eine Funktion verläuft. Wenn das m positiv ist, steigt die Funktion an und wenn das m negativ ist, fällt sie.
Lineare Funktionen Steigung
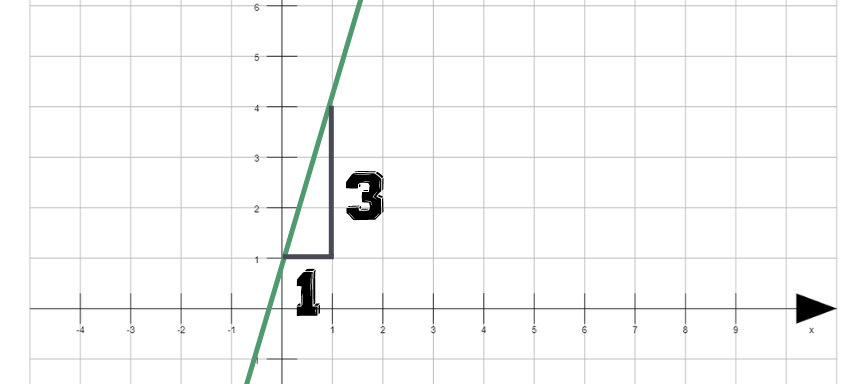
Nun weißt du schon, was die Steigung ist und wo du sie in der Formel findest. Vielleicht fragst du dich aber, wie du aus einer Zeichnung die Steigung bestimmst. Dazu brauchst du ein sogenanntes Steigungsdreieck.
Du wählst also 2 Punkte auf der Geraden aus und zeichnest das Dreieck an diese Punkte dran.
Dann schaust du wie lang die beiden Seiten des Dreiecks sind, die du gerade an die Funktion dran gezeichnet hast. Anschließend teilst du die Länge der senkrechten Linie durch die Länge der waagerechten Linie.
Beispiel: 3 / 1 = 3
Die Steigung ist also 3.

Lineare Funktionen – Berechnen der Steigung
Mit den beiden Punkten die du auf der Geraden ausgesucht hast, kannst du die Steigung auch berechnen. Punkt 1 ist ( 0 / 1 ), somit ist \displaystyle x_1=0 und \displaystyle y_1=1. Der zweite Punkt den wir ausgesucht hatten ist ( 1 / 4 ). Deshalb ist \displaystyle x_2=1 und \displaystyle y_2=4.
Nun rechnest du \displaystyle \frac{y_2-y_1}{x_2-x_1}.
Wenn du jetzt die Werte einsetzt erhältst du \displaystyle \frac{4-1}{1-0}=3.
Lineare Funktionen zeichnen
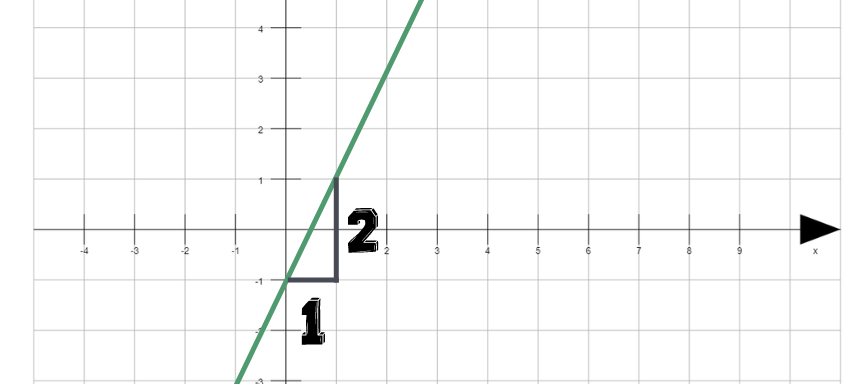
Gegeben ist die Funktion f ( x ) = 2 x – 1.
Der y-Achsenabschnitt ist -1. Somit markierst du den Punkt (0/- 1) auf der y-Achse. Von dort gehst du 1 nach rechts und 2 nach oben, weil die Steigung positiv ist. Wäre die Steigung negativ, würdest du 2 nach unten gehen.
Lineare Funktionen – Nullstellen bestimmen
Nullstellen sind die Schnittpunkte einer Funktion mit der x-Achse. Lineare Funktionen haben meistens genau eine Nullstelle.
Ausnahmen sind lineare Gleichungen mit m = 0. Diese Gleichungen sind waagerecht und haben keine Nullstellen oder unendlich viele, wenn b = 0. Dies liegt daran, dass die Funktion f ( x ) = 0 x + 0 auf der x-Achse liegt.
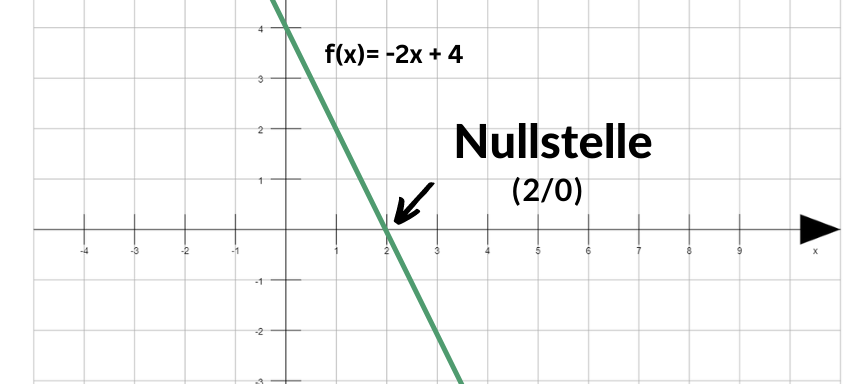
Um nun die Nullstelle zu berechnen, setzt du die Funktion gleich Null:
– 2 x + 4 = 0
Dies löst du nach x auf:
– 2 x + 4 = 0 | – 4
⇔ – 2 x = – 4 | : ( – 2 )
⇔ x = 2
Die Nullstelle ist ( 2 / 0 ).
Lineare Gleichungen Aufgaben
Jetzt hast du das Wichtigste zum Thema ‘Lineare Gleichungen’ gelernt. Damit du dein Wissen verfestigen kann, findest du hier direkt Übungen.
Viel Spaß damit!
Aufgabe 1
Stelle die lineare Gleichung auf.
a ) Eine lineare Funktion hat die Steigung 4 und der y-Achsenabschnitt liegt bei – 3.
b ) Die Steigung beträgt – 6 und die Funktion schneidet die y-Achse bei 4.
c ) Eine Funktion hat den y-Achsenabschnitt 1 und verläuft durch die Punkte A ( 0 / 1 ) und B ( 1 / 6 ).
d ) Die Funktion verläuft durch A ( 1 / 1 ) und B ( 2 / 2 ). Der y-Achsenabschnitt befindet sich im Ursprung.
e ) Die y-Achse wird von der Funktion bei 2 geschnitten und die Steigung beträgt 1,5.
f ) Die Steigung der Funktion ist genau 1 und der y-Achsenabschnitt liegt bei – 3,25.
g ) Die Funktion verläuft durch die Punkte A ( 0 / – 4 ) und B ( 2 / 12 ).
h ) Die Funktion verläuft durch die Punkte A ( – 1 / – 1 ) und B ( 1 / 1 ).
Lösung 1
a ) Eine lineare Funktion hat die Steigung 4 und der y-Achsenabschnitt liegt bei – 3.
f ( x ) = 4 x – 3
b ) Die Steigung beträgt – 6 und die Funktion schneidet die y-Achse bei 4.
f ( x ) = – 6 x + 4
c ) Eine Funktion hat den x-Achsenabschnitt 1 und verläuft durch die Punkte A ( 0 / 1 ) und B ( 1 / 6 ).
m = \displaystyle \frac{6 - 1}{1 - 0}=5
f ( x ) = 5 x + 1
d ) Die Funktion verläuft durch A ( 1 / 1 ) und B ( 2 / 2 ). Der y-Achsenabschnitt befindet sich im Ursprung.
\displaystyle \frac{2 - 1}{2 - 1}=1
f ( x ) = 1 x + 0
e ) Die y-Achse wird von der Funktion bei 2 geschnitten und die Steigung beträgt 1,5.
f ( x ) = 1,5 x + 2
f ) Die Steigung der Funktion ist genau 1 und der y-Achsenabschnitt liegt bei – 3,25.
f ( x ) = 1 x – 3,25
g ) Die Funktion verläuft durch die Punkte A ( 0 / – 4 ) und B ( 2 / 12 ).
Der Punkt A ist der Schnittpunkt mit der y-Achse. Der y-Achsenabschnitt liegt also bei – 4.
f ( x ) = 8 x – 4
h ) Die Funktion verläuft durch die Punkte A ( – 1 / – 1 ) und B ( 1 / 1 ).
Diese Funktion schneidet die y-Achse im Ursprung, also im Punkt ( 0 / 0 ).
f ( x ) = 1 x + 0
oder auch einfach nur
f ( x ) = x
Aufgabe 2
Berechne die Steigung mit 2 Punkten, die auf der Gerade liegen.
a ) A ( 0 / 2 ) und B ( 1 / – 3 )
b ) A ( 2 / 1 ) und B ( 3 / 0 )
c ) A ( 0 / – 2 ) und B ( 1 / – 5 )
d ) A ( 0 / 1 ) und B ( 1 / 6 )
e ) A ( – 3 / – 2 ) und B ( – 1 / – 5 )
Lösung 2
a ) A ( 0 / 2 ) und B ( 1 / – 3 )
m = \displaystyle \frac{(-3)-2}{1-0}=-5
b ) A ( 2 / 1 ) und B ( 3 / 0 )
m = \displaystyle \frac{0-1}{3-2}=-1
c ) A ( 0 / – 2 ) und B ( 1 / – 5 )
m = \displaystyle \frac{(-5)-(-2)}{1-0}=-3
d ) A ( 0 / 1 ) und B ( 1 / 6 )
m = \displaystyle \frac{6 - 1}{1 - 0}=5
e ) A ( – 3 / – 2 ) und B ( – 1 / – 5 )
m = \displaystyle \frac{(-5)-(-2)}{(-1)-(-3)}=-1,5
Aufgabe 3
Bestimme die Nullstellen.
a ) f ( x ) = 2 x – 8
b ) f ( x ) = 0,5 x + 2
c ) f ( x ) = 4 x – 1
d ) f ( x ) = 5,5 x – 11
Lösung 3
a ) f ( x ) = 2 x – 8
x = 4
b ) f ( x ) = 0,5 x + 2
x = – 4
c ) f ( x ) = 4 x – 1
x = 0,25
d ) f ( x ) = 5,5 x – 11
x = 2
Lineare Gleichungen – FAQ
Hier findest du noch einmal alles Wichtige im Überblick:
Was ist eine lineare Funktion?
Lineare Gleichungen kann man auch Gleichungen ersten Grades oder lineare Funktion nennen, weil die Variabel nur in der ersten Potenz vorkommt. Wenn diese Variabel x ist, heißt das, dass es keine Teile mit x², x³ und so weiter gibt, sondern nur x.
Beispiele:
f ( x ) = 3 x + 5
g ( x ) = 2 x – 4
Wenn du lineare Funktionen zeichnest, erhältst du eine gerade Linie.
Wie berechnet man die Steigung m?
m = \displaystyle \frac{y_2-y_1}{x_2-x_1}
Die allgemeine Formel für lineare Gleichungen lautet f ( x ) = m x + b.
Die Steigung steht in m. Dadurch wird erklärt, wie flach oder steil eine Funktion verläuft. Wenn das m positiv ist, steigt die Funktion an und wenn das m negativ ist, fällt sie.
Wie kann man die Steigung ablesen?
Die Steigung kann man mit einem Steigungsdreieck ablesen.
Für ein Steigungsdreieck wählst du also 2 Punkte auf der Geraden aus und zeichnest das Dreieck an diese Punkte dran. Dann schaust du wie lang die beiden Seiten des Dreiecks sind, die du gerade an die Funktion dran gezeichnet hast. Dann teilst du die Länge der senkrechten Linie durch die Länge der waagerechten Linie.
Beispiel: 3 / 1 = 3
Die Steigung ist also 3.
Welche linearen Funktionen haben keine Nullstellen?
Wenn die Funktion waagerecht verläuft und die Steigung also Null ist, hat die lineare Funktion keine Nullstellen.
Nullstellen sind die Schnittpunkte einer Funktion mit der x-Achse. Lineare Funktionen haben meistens genau eine Nullstelle. Ausnahmen sind lineare Gleichungen mit m = 0. Diese Gleichungen sind waagerecht und haben keine Nullstellen oder unendlich viele, wenn b = 0. Dies liegt daran, dass die Funktion f ( x ) = 0 x + 0 auf der x-Achse liegt.
Lineare Funktionen - Was ist m?
Das m ist die Steigung der Funktion. Dadurch wird erklärt, wie flach oder steil eine Funktion verläuft. Wenn das m positiv ist, steigt die Funktion an und wenn das m negativ ist, fällt sie.
Lineare Funktionen - Was ist b?
Das b beschreibt den y- Achsenabschnitt. Das ist also der Punkt, an dem die lineare Funktion die y-Achse schneidet.


Sehr interesanter Beitrag, danke fürs veröffentlichen. Mfg. Lineargott
Ich habe es immernoch nich kapiert
fühl ich bruder
Ich fande den Artikel sehr hilfreich. Ich habe jetzt alles verstanden
hatte letzetns eine gleichzng 4y=3*x-2. was soll ich mit der 4y anfangen?
Hallo Jany,
x ist die unabhängige Variable, für die man Werte z.B. aus dem Bereich [ 0, …, 10 ] einsetzen kann.
y = ist die abhängige Variable, d.h. die Ergebnisvariable!
4y=3*x-2 ist eine lineare Gleichung 1. Grades, d.h. es wird nur mit x und NICHT mit x hoch 2 (= 2. Grades) gerechnet.
Auf der linken Seite der Gleichung wird mit y das Ergebnis der Berechnung der Gleichung ausgegeben, auf der rechten Seite der Gleichung wird mit x gerechnet. Dabei kann man z.B. für x bestimmte Werte wie z.B. aus dem Bereich [ 0, …, 10 ] einsetzen. Für jeden Wert x bekommt man ein anderes Ergebnis y (Stichwort: Wertetabelle).
Bei der Gleichung 4y=3*x-2 sind beiden Seiten (links und rechts) der Gleichung gleich, im Sinne von “im Gleichgewicht”. Die linke Seite mit 4y ist quasi vier mal “größer” als die rechte Seite der Gleichung (= Balkenwaage). Trotzdem ist die Waage (= Gleichung) im Gleichgewicht!
Bei Gleichungen (= Gleichgewicht der Balkenwaage) müssen Rechenoperatoren bei der Gleichung stets auf beiden(!) Seiten der Gleichung vorgenommen werden, damit die Gleichung quasi im Gleichgewicht bleibt:
4y = 3 * x – 2 | : 4
y = 3/4 * x – 2/4
= 1/4 * ( 3 * x – 2 )
Für x = 0 erhält man:
y = 1/4 * ( 3 * 0 – 2 )
= 1/4 * (-2) = – 1/2
Probe:
4y = 3 * x – 2
4 * (-1/2) = 3 * 0 – 2
– 2 = -2 ~> richtig gerechnet!
Für x = 4/3 erhält man:
4y = 3 * x – 2 | : 4
y = 3/4 * x – 1/2
= 3/4 * 4/3 – 1/2
= 1 – 1/2 = 1/2 = 0,5
Probe:
y = 3/4 * x – 1/2
0,5 = 3/4 * 4/3 – 1/2
= 1 – 1/2
= 1/2
= 0,5 ~> richtig gerechnet!
Beachte:
Punktrechnung geht vor Strichrechnung!
4y = 3 * x – 2 4y = 3x – 2
4y = 3 * ( x – 2 ) ist ungleich(!) 4y = 3x – 2
Die Klammer bei 3 * ( x – 2 ) hebt praktisch die Regel “Punktrechnung geht vor Strichrechnung!” vorübergehend auf! Aber eben nur das eine Mal.
Viel Erfolg wünscht Dieter
Alles kapiert! Ist ja wirklich logisch und einfach.
Vielen Dank für die Aufschlüsselung all meiner Fragezeichen!