Fragst du dich, was eine Kurvendiskussion ist? Bist du dir unsicher, welche Eigenschaften einer Funktion man untersuchen kann?
Wir zeigen dir Schritt für Schritt anhand von Beispielen, wie du eine Kurvendiskussion richtig durchführst, und worauf du dabei ganz besonders achten musst.
Bei einer Kurvendiskussion werden folgende Eigenschaften einer Funktion untersucht:
- Der Definitionsbereich
- Die Extremstellen
- Die Sattelpunkte
- Die Wendepunkte
- Die Nullstellen
- Der Achsenabschnitt
- Die Symmetrieeigenschaft
- Das Monotonieverhalten
Schauen wir uns dazu zwei Beispiele an.
In die Funktion f(x) = 4x3 + 2x2 – 4x + 3 lassen sich alle Zahlen einsetzen. Dabei spielt es keine Rolle, ob die Zahlen positiv, negativ, groß oder klein sind. Der Definitionsbereich lautet: Df = ( –∞ , ∞)
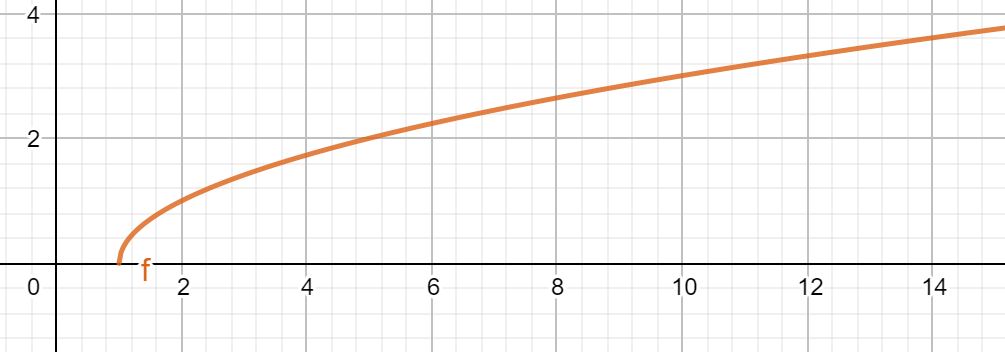
Bei der Funktion sieht dies anders aus. Wir können die Wurzel aus einer negativen Zahl nicht ziehen. Das bedeutet, dass wir unter die Wurzel für x nur Zahlen einsetzen dürfen, bei denen x +1 ≥ 0 ist. Damit ergibt sich ein Definitionsbereich von
Df = [-1 ,∞) wobei -1 die kleinste Zahl ist, die wir einsetzen dürfen.
Extremstellen bestimmen
Bei einer Kurvendiskussion werden auch immer die Extremstellen bestimmt. Hierzu zählen Hochpunkte und Tiefpunkte.
Um unsere Funktion auf Extremstellen zu untersuchen bilden wir zunächst die erste Ableitung.
f(x) = 4x3+ 2x2 – 4x + 3
f´(x) = 12x2 + 4x – 4
Nun setzen wir die erst Ableitung der Funktion gleich 0.
f´(x) = 12x2 + 4x – 4 = 0
Um diesen Term nach x aufzulösen verwenden wir die pq-Formel.
Dazu teilen wir zunächst unseren Term durch 12, um vor dem x2 keine Zahl stehen zu haben.
x2+ ⅓ x – ⅓ = 0
x1 = 0,43
x2 = -0,767
Damit habe wir rausgefunden, bei welchem x-Wert sich die Extremstellen der Funktion befinden. Um herauszufinden, ob es sich dabei um Hoch- oder Tiefpunkte handelt, bilden wir die zweite Ableitung und setzen die x-Werte ein.
f´´(x) = 24x + 4
f´´(0,43) = 14,32 → Tiefpunkt
f´´(-0,767) = -14,408 → Hochpunkt

Sattelpunkt berechnen
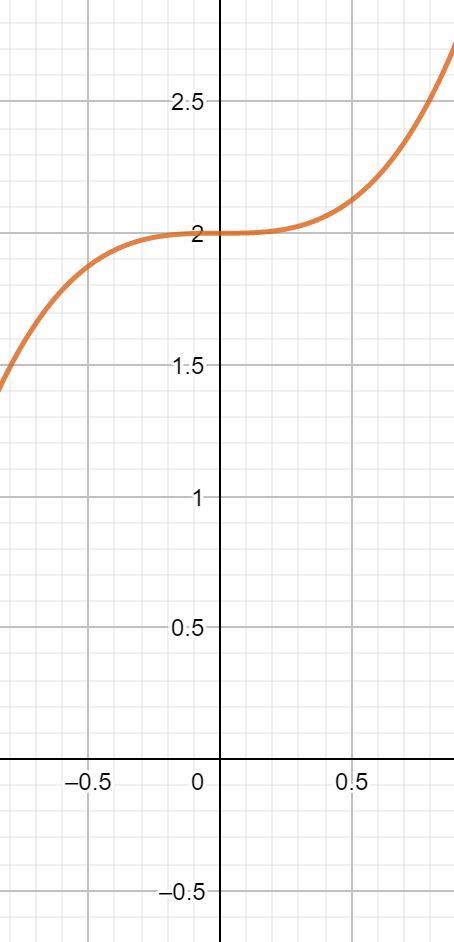
Dazu untersuchen wir die Funktion f(x) = x3 +2 auf einen Sattelpunkt. Zunächst bilden wir die ersten drei Ableitungen der Funktion.
f´(x) = 3x2
f´´(x) = 6x
f´´´(x) = 6
Nun setzten wie die erste Ableitung gleich Null und berechnen den x-Wert der Extremstelle.
f´(x) = 0
x = 0
Im zweiten Schritt setzen wie diesen Wert in die zweite Ableitung ein, und schauen, ob die zweite Ableitung an der x-Stelle gleich 0 ist.
f´´(0) = 6*0 = 0
Im letzten Schritt überprüfen wir, ob die dritte Ableitung der Funktion ungleich 0 ist. Da diese Ableitung immer 6 ergibt, unabhängig von der eingesetzten Zahl, ist die dritte Ableitung immer ungleich 0. Somit haben wir an der Stelle x = 0 einen Sattelpunkt.
Wendestelle berechnen
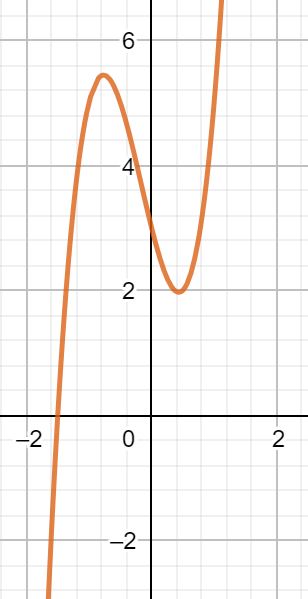
Wir untersuchen die Funktion f(x) = 4x3 + 2x2 – 4x + 3 auf eine Wendestelle.
Im ersten Schritt bilden wir dazu die zweite und dritte Ableitung der Funktion
f´´(x) = 24x + 4
f´´´(x) = 24
Nun bestimmen wir die Nullstelle der zweiten Ableitung. Also die Nullstelle einer linearen Funktion.
f´´(x) = 24x + 4 = 0
x = -⅙
Im letzten Schritt überprüfen wir, ob die dritte Ableitung ungleich 0 ist. Da die dritte Ableitung unabhängig von der Zahl, die wir einsetzen immer gleich 24 ist, ist die dritte Ableitung ungleich Null. Somit haben wir an der Stelle x = -⅙ ein Wendepunkt vorliegen.
Nullstellen einer Funktion bestimmen
Um die Nullstelle einer Funktion zu bestimmen setzen wir also die Funktion gleich Null.
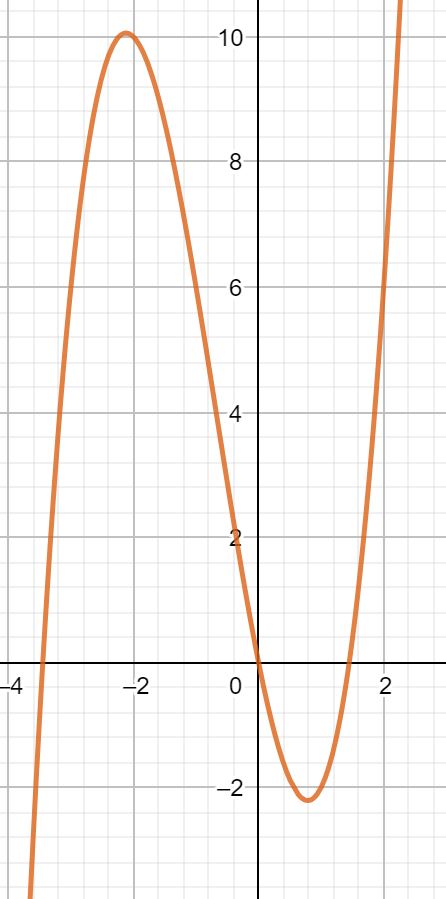
f(x) = x3+ 2x2– 5x = 0 |ausklammern
f(x) = x* (x2 + 2x – 5) → Damit ist eine Nullstelle der Funktion der Punkt P (0|0)
f(x) = x2 + 2x – 5 → Die Nullstelle dieser Funktion lässt sich mit Hilfe der pq-Formel berechnen
x1 = 1,45 und x2 = -3,45
Die Nullstellen der Funktion lauten P(0|0), Q(1,45|0) und R(-3,45|0)
y-Achsenabschnitt berechnen
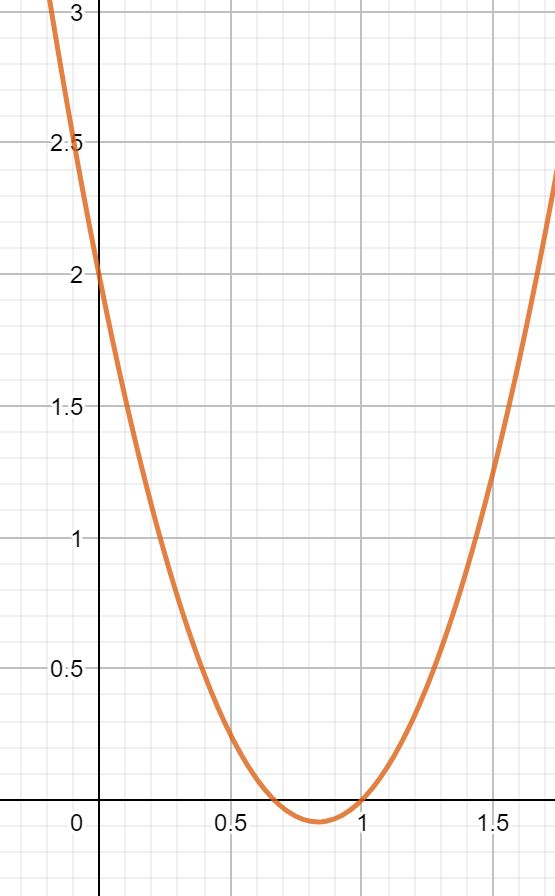
Der Achsenabschnitt einer Funktion sagt aus, wann die Funktion die y-Achse schneidet.
f(x) = 3x2 – 5x +2
Um den Achsenabschnitt zu berechnen, setzen wir für jedes x eine 0 ein.
f(0) = 3*02 – 5*0 +2 = 2
Der Achsenabschnitt dieser Funktion liegt bei A(0|2)
Symmetrieeigenschaft
Als letztes können wir bei einer Kurvendiskussion Funktionen auf ihre Symmetrieeigenschaft untersuchen. Sie können entweder Punktsymmetrisch zum Ursprung oder Achsensymmetrisch zur y-Achse sein.
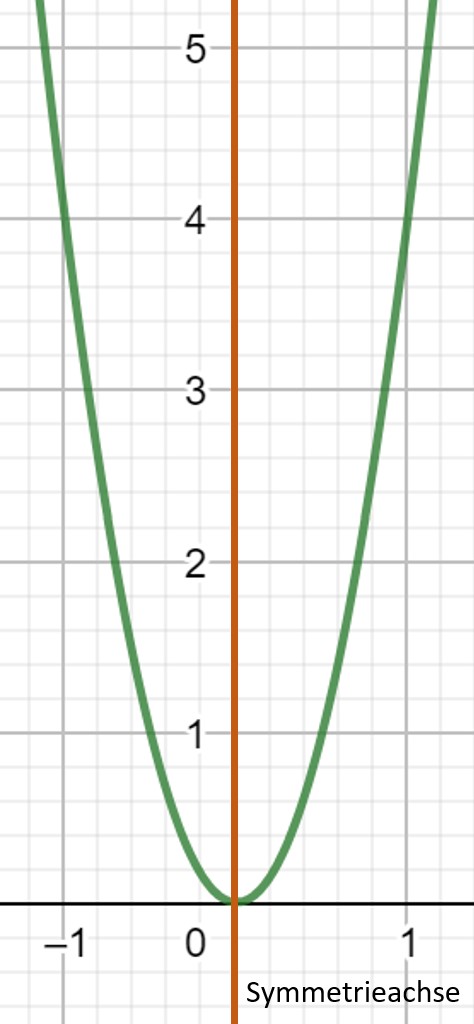
Wenn von Achsensymmetrie die rede ist, bezieht man sich immer darauf, dass die y-Achse die Symmetrieachse ist. Eine Funktion ist immer dann achsensymmetrisch, wenn sie nur gerade Exponenten enthält.
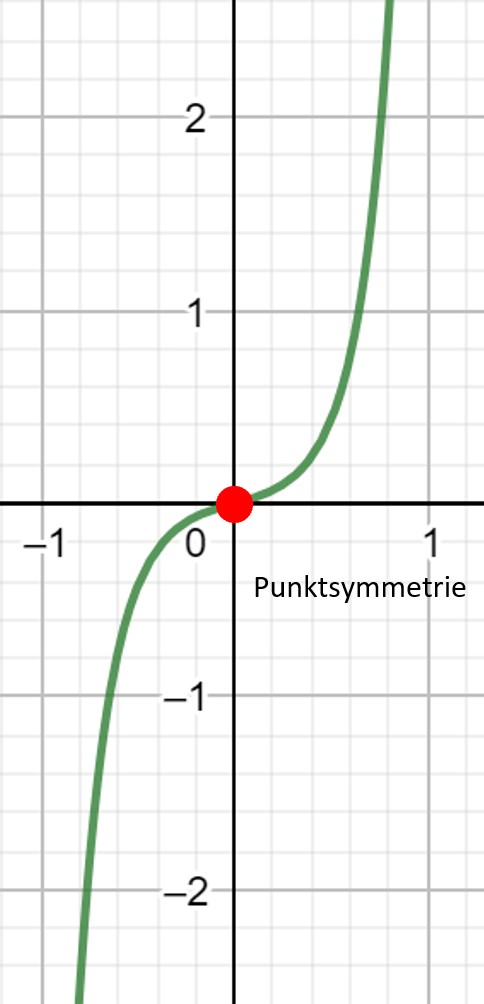
Das bedeutet, dass eine Funktion immer dann punktsymmetrisch zum Ursprung ist, wenn sie nur ungerade Exponenten enthält.
Dabei darf die Funktion keine Konstante haben, da sonst die Punktsymmetrie zum Ursprung nicht mehr gegeben ist.
Zunächst überprüfen wir diese Funktion auf Achsensymmetrie. Dazu setzen wir einen beliebigen Wert für x ein und rechnen den Wert der Funktion an dieser Stelle aus. Danach setzen wir erneut den gleichen Wert in die Funktion ein drehen aber das Vorzeichen und berechnen den Wert der Funktion.
Nehmen wir zum Beispiel den Wert 3 und -3
f(x) = 3∗x4 – 5∗x2 +2
f(3) = 3∗34 – 5∗32 +2 = 200
f(-3) = 3∗(-3)4 – 5∗(-3)2 +2 = 200
Da bei beiden Berechnungen der Wert 200 rauskommt, ist die Funktion Achsensymmetrisch zum Ursprung.
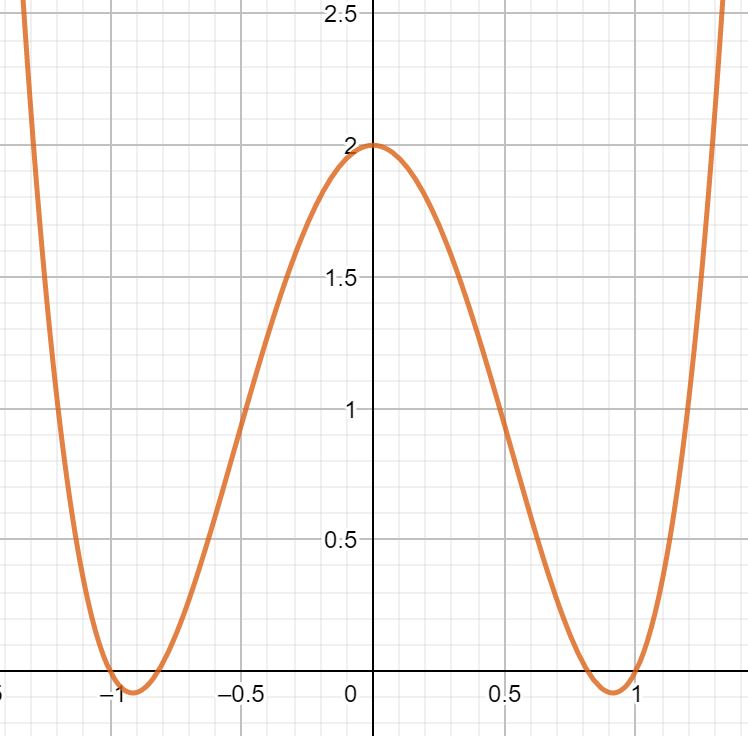
Monotonieverhalten
Bei der Monotonie findest du heraus, ob eine Funktion in einem bestimmten Bereich steigt oder fällt.
Das Monotonieverhalten wird dann wie folgt definiert und durch die 1. Ableitung ermittelt:
Funktion f ist:
- streng monoton steigend, wenn f´(x) > 0
- monoton steigend, wenn f´(x) ≥ 0
- streng monoton fallen, wenn f´(x) < 0
- monoton fallend, wenn f´(x) ≤ 0
Daraus kannst du ablesen: Wenn die erste Ableitung einer Funktion nie gleich null ist, dann wird sie streng monoton fallend oder steigend genannt.
FAQ Kurvendiskussion
Welche Schritte muss ich bei einer Kurvendiskussion durchführen?
Falls nicht explizit nach nur einem bestimmten Schritt gefragt wird, kannst du folgende Schritte zur Berechnung durchführen:
- Definitionsbereich
- Extremstellen
- Sattelpunkte
- Wendepunkte
- Nullstellen
- Achsenabschnitt
- Symmetrieeigenschaft
Wofür brauche ich eine Kurvendiskussion?
Die Durchführung einer Kurvendiskussion hilft dir dabei eine Funktion, bei der du nur die Funktionsgleichung gegeben hast zu zeichnen. Du kannst Punkte, wie Nullstellen, Hoch- und Tiefpunkte oder auch Wendestellen dazu nutzen, eine Funktion leichter zeichnen zu können.
Du findest weitere hilfreiche Erklärungen zu verschiedenen Themengebieten auf der Homepage des Nachhilfe-Teams.

Bei der Achsensymmetrie (Klappsymmetrie) ist ein kleiner Fehler unterlaufen:
Sie geben vor: f(x)=3x^4– 5x^2 +2 als Funktion, aber dann sind beim Einsetzen des Wertes 3 die Klammern falsch gesetzt (es müsste lauten 3*(3^4) – 5*(3^2) +2 = 200, wenn man schon Klammern setzen will). Das Ergebnis ist aber richtig.
Nach Ihrer Rechnung müsste gelten 9^4 – 15^2 + 2 also 6561 -225 +2 =6338!
Mit freundlichem Gruß aus dem schönen Saarland
und auch herzlichen Dank für die ausführliche Darstellung einer Kurvendiskussion (muss viel Mühe gekostet haben!! Toll gemacht!!
Gruß Robert Bost
Danke für das Anmerken des Fehlers und für dein nettes Feedback Robert 🙂
Wir haben den Fehler ausgebessert und auch die Klammern weggelassen, denn wie du schon sagst müssen die nicht sein.
Liebe Grüße zurück ins Saarland und schau doch mal bei unseren anderen Mathe-Artikeln vorbei.
Dein Nachhilfe-Team