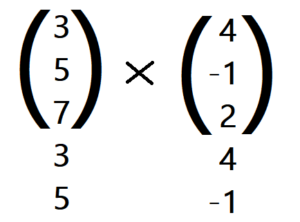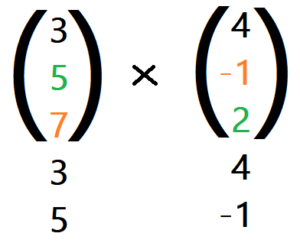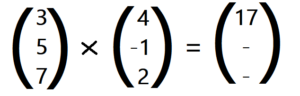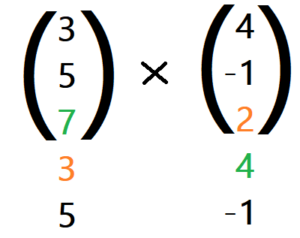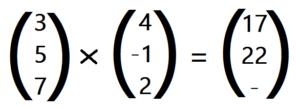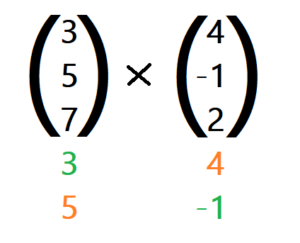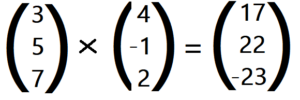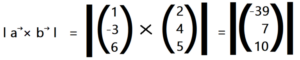4,29 von 5 Sterne
Loading...
Loading...Du musst im Matheunterricht das Kreuzprodukt von zwei Vektoren bestimmen? Aber du weißt nicht wie du die entsprechende Formel anwendest ? Dann bist du hier richtig. In diesem Artikel zeigen wir dir wie Du das Kreuzprodukt problemlos anwenden kannst.
Kreuzprodukt Formel
Damit du das Kreuzprodukt zweier Vektoren ermitteln kannst, brauchen wir die entsprechende Formel.
Diese lautet:
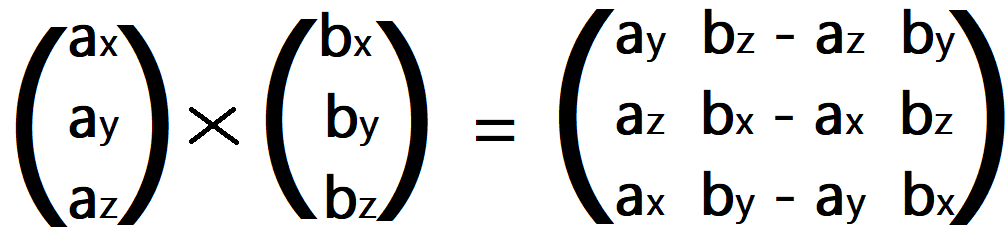
Du rechnest x ohne die x-Zeile aus (Variable ax und bx)
Du rechnest y ohne die y-Zeile aus (Variable ay und by)
Du rechnest z ohne die z-Zeile aus (Variable az und bz)
Kreuzprodukt berechnen – Schritt für Schritt erklärt
Im folgenden Beispiel zeigen wir dir einen Trick, damit du die Formel nicht auswendig lernen musst.
Kreuzprodukt – Beispiel: Für die beiden Vektoren und soll das Vektorprodukt berechnet werden.
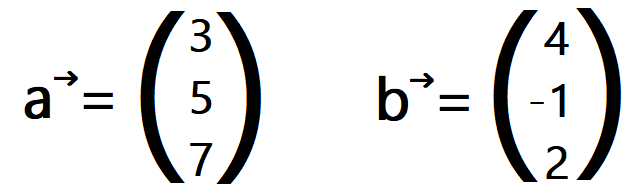
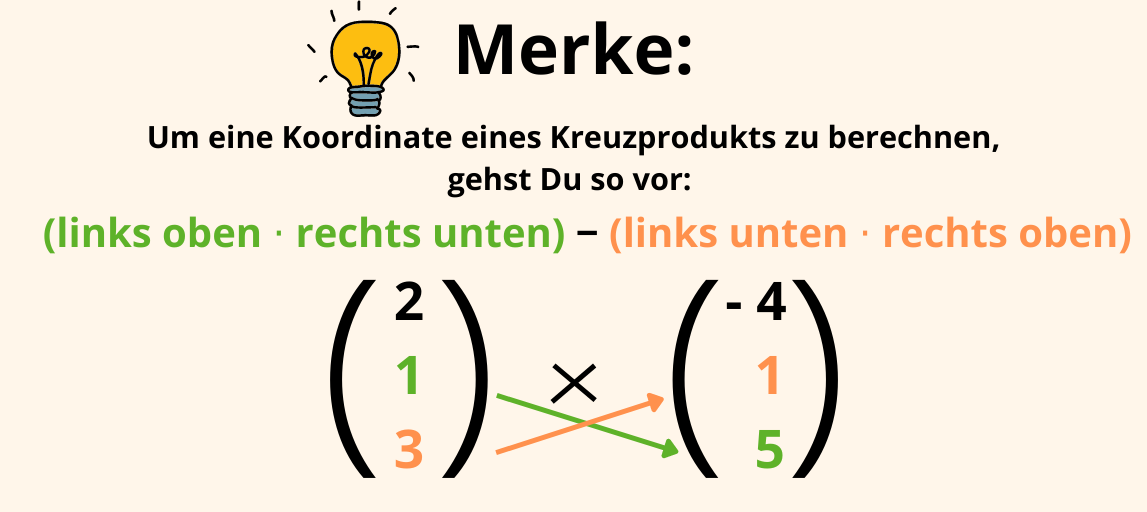
1. Du schreibst die oberen zwei Zeilen der Vektoren noch einmal unter die Vektoren.
2. Anschließend rechnest du nacheinander (kreuzweise) die einzelnen Koordinaten des Vektorprodukts aus. Du beginnst mit der 2. und 3. Zeile und multiplizierst die Koordinaten von links oben nach rechts unten. Davon ziehst du dann das Produkt der Koordinate von links unten nach rechts oben.
Du rechnest die erste Koordinate folgendermaßen aus:
5 ⋅ 2 – 7 ⋅ (- 1) = 17 , also 
3. Nun hast du die erste Zeile des neuen Vektors. Wir führen dasselbe Verfahren durch, um die zweite Zeile des Vektors herauszufinden. Hier fängst du in der 3. und 4. Zeile an, also rücken wir eine Zeile nach unten.
So rechnest du die zweite Koordinate aus:
7 ⋅ 4 – 3 ⋅ 2 = 22 , also 
4. Das gleiche Schema führst du wieder fort, um unsere letzte Koordinate herauszufinden. Wir rücken wieder eine Zeile nach unten und beginnen mit der 4. und 5. Zeile.
Die letzte Koordinate rechnest du so aus:
3 ⋅ (- 1) – 5 ⋅ 4 = – 23 , also 
Du erhältst Deine letzte Koordinate vom Vektorprodukt. Somit hast Du das Kreuzprodukt der beiden Vektoren und berechnet.
Kreuzprodukt Eigenschaften
Es gibt drei Eigenschaften des Kreuzprodukts, die wir dir in diesem Kapitel veranschaulichen.
– Das Kreuzprodukt ist nicht kommutativ. Werden bei der Berechnung die Vektoren und vertauscht, ändert sich das Vorzeichen. Die Länge des Ergebnisvektors bleibt jedoch gleich, aber das Ergebnis zeigt in entgegengesetzter Richtung (Gegenvektor). Die Reihenfolge ist also von großer Bedeutung.
× = – ( × ) bzw. × = – ×
– Für das Kreuzprodukt gilt das Distributivgesetz:
× ( + ) = × + ×
– Das Vektorprodukt ist nicht assoziativ.
c ( × ) = ( c ) × = × ( c )
Betrag eines Kreuzprodukts berechnen
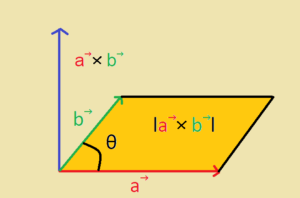
In diesem Abschnitt zeigen wir Dir wie man den Betrag des Kreuzprodukts und berechnen kann. Dieser ist gleich der Fläche des Parallelogramms, welcher von den entsprechenden Vektoren aufgespannt wird.
Beispiel: Wir sollen den Flächeninhalt berechnen, welche die zwei Vektoren aufspannen.
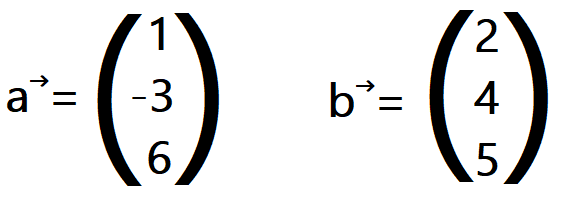
Zuerst berechnest du das Vektorprodukt der zwei Vektoren und bildest anschließend den Betrag davon. Hierfür quadrierst du den x-Wert, den y-Wert und den z-Wert unter der Wurzel.
A = √(- 39)² + 7² + 10²
= √1521 + 49 + 100
= √1670
= 40, 87 FE
Du bekommst eine Fläche von 40,87 Flächeneinheiten (FE) , die die beiden Ausgangsvektoren aufspannen.
Kreuzprodukt – Aufgaben
Rechne die Aufgaben und schaue, ob du die Formel für das Kreuzprodukt richtig anwendest. Anschließend kannst du deine Lösung überprüfen. Klicke einfach auf die Links und schon öffnen sich die Dateien.
Viel Erfolg!
FAQ
Was sagt das Kreuzprodukt aus?
Bei einem Kreuzprodukt zweier Vektoren erhält man einen dritten Vektor, der senkrecht auf den beiden Ausgansvektoren steht.
Ist Vektorprodukt und Kreuzprodukt das gleiche?
Das Vektorprodukt wird oft auch als “Kreuzprodukt” bezeichnet. Das Vektorprodukt ist die multiplikative Verknüpfung zweier Vektoren. Das Ergebnis ist ebenfalls ein Vektor, der senkrecht auf den beiden Vektoren steht.
Dieser Artikel könnte dich auch interessieren:
Hat dir unser Artikel gefallen? Wir würden uns sehr freuen, wenn du uns eine Sternebewertung hinterlässt. Vielen Dank!☺️
4,29 von 5 SterneLoading...
