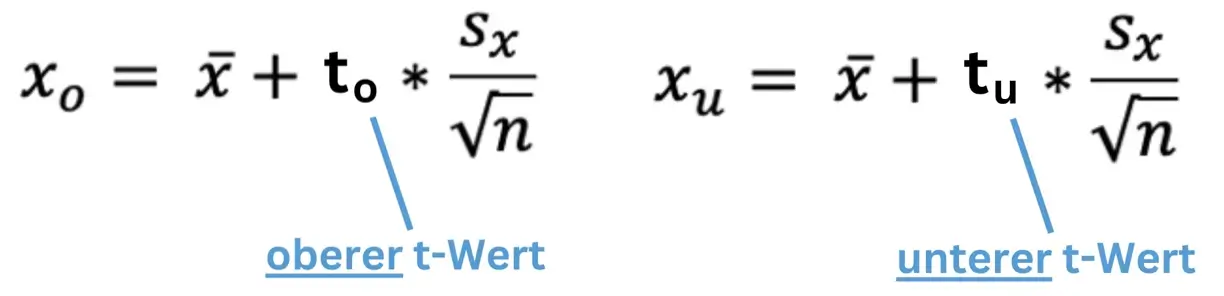5,00 von 5 Sterne
Loading...
Konfidenzintervalle sind dir eher ein Rätsel statt eine Hilfe? Das Gefühl kennen wir, deshalb erklären wir dir hier Schritt für Schritt das Wichtigste, sodass dir Konfidenzintervalle in der Zukunft unter die Arme greifen statt dich verzweifeln zu lassen!
Du findest im Folgenden …
… eine einfache Erklärung von Konfidenzintervallen und wozu wir sie brauchen
… die Formeln die wir zum Rechnen brauchen einfach und anschaulich zerlegt
… Erklärungen und Berechnungen des 95 und 99 Konfidenzintervalls
… wie eine gelungene Interpretationen dieser Konfidenzintervalle aussieht
Frage: Durchschnittliche Größe Koi-Karpfen?
Deine Familie hat einen Teich mit etwa 100 Koi-Karpfen. Du fragst dich wie groß eure 100 Karpfen im Durchschnitt sind.
Dein Vorgehen:
- Du untersuchst 10 der Fische diese bilden deine Stichprobe.
- Du ermittelst den Mittelwert x̄ deiner Stichprobe und findest heraus, dass diese 10 Fische im Durchschnitt 42 cm groß sind.
Problem: Wahrer Mittelwert?
- Der Mittelwert der Stichprobe x̄ ist nur eine Schätzung des Wahren Mittelwerts μ in der Grundgesamtheit (= alle 100 Fische).
- Du möchtest dich aber nicht auf eine Schätzung verlassen und bringst den Konfidenzintervall ins Spiel!
Weiteres Vorgehen:
- Mit dem Konfidenzintervall bestimmst du den Bereich des wahren Mittelwerts (= Durchschnittl. Größe der 100 Fische)!
- Du berechnest einen 95 Konfidenzintervall und erhältst den Bereich 40cm – 50cm.
Jetz weißt du, dass die durchschnittliche Größe aller 100 Koi-Karpfen mit einer 95%-Wahrscheinlichkeit zwischen 40 und 50 Zentimetern liegt!
Der Kofidenzintervall hilft uns also dabei einen Bereich zu bestimmen in dem unser Parameter (=Durchschnittliche Größe der Koi-Karpfen) in der Grundgesamtheit (= alle Koi Karpfen im Teich) liegen muss. Dieser Bereich ist immer so verlässlich wie das bestimmte Konfidenzniveau (=95 bzw. 95%).
Wenn wir das Konfidenzniveau erhöhen (z.B. 99%) dann ist unser Bereich zuverlässiger aber auch zwangsläufig größer! Wenn wir die Stichprobengröße erhöhen (=mehr Koi-Karpfen untersuchen), dann wird unser Bereich kleiner und genauer!
Übersicht wichtiger Begriffe
Falls dir einige Begriffe im Text nicht mehr oder noch nicht geläufig sind haben wir dir hier eine Liste der wichtigsten zusammengestellt!
Beispieluntersuchung: Durchschnttl. Größe von Frauen
Definition
Einheiten, die für unsere Untersuchung relevant sind.
Bedeutung für Beispieluntersuchung:
Alle Frauen
Definition
Einheiten die der Grundgesamtheit für unsereUntersuchung entnommen wurden.
Bedeutung für Beispieluntersuchung:
Die für die Untersuchung ausgewählten Frauen.
Definition
Anzahl der Einheiten in der Stichprobe.
Bedeutung für Beispieluntersuchung:
Anzahl der für die Untersuchung ausgewählten Frauen.
Definition
Der durchschnittliche Wert unserer Stichprobe.
Bedeutung für Beispieluntersuchung:
Durchschnttl. Größe der für die Untersuchung ausgewählten Frauen.
Definition
Maß für die Streuung von Werten der Einheiten, um den Mittelwert der Stichprobe herum.
Bedeutung für Beispieluntersuchung:
Die mittlere Abweichung von Größen (in cm) um die durchschnittliche Größe der für die Untersuchung ausgewählten Frauen.
Definition
Der tatsächliche Wert eines Parameters (z.B. Mittelwert) in der Grundgesamtheit.
Bedeutung für Beispieluntersuchung:
Die tatsächliche durchschnittliche Größe aller Frauen i.d. Welt
Definition
Wahrscheinlichkeit (z.B. 95%) mit der der wahre Wert innerhalb des Konfidenzintervalls liegt.
Bedeutung für Beispieluntersuchung:
Wahrscheinlichkeit (z.B. 95%) mit der die durchschnittliche Größe von Frauen i.d. Welt innerhalb des von uns bestimmten Konfidenzintervalls liegt.
Definition:
Grundgesamtheiten von denen die wahre Standardabweichung bekannt ist → der Fall wenn bereits viel zu diesen Grundgesamtheiten geforscht wurde und wiederholt festgestellt wurde, dass die Werte sich in einem gewissen Muster streuen.
Bedeutung für Beispieluntersuchung:
Zur Körpergröße von Menschen ist beispielsweise bekannt, dass diese konstant um einen gewissen Mittelwert streuen. D.h. die meisten Menschen sind ähnlich groß und Ausreißer sind hier eher selten → Körpergröße von Menschen ist normalverteilt.
Definition:
Im Vergleich zur Normalverteilung ist bei der T-Verteilung keine wahre Standardabweichung bekannt. Dies hat zur Folge, dass wir die Stichprobengröße einen Einfluss auf die Genaugigkeit unseres Konfidenzintervalls hat. (Je höher desto besser)
Bedeutung für Beispieluntersuchung:
Keine, da normalverteilt.
Konfidenzintervall Formel
Normalverteilung – Formel
Um mit Hilfe eines Konfidenzintervall den Bereich ermitteln in dem der wahre Mittelwert einer normalverteilten Grundgesamtheit liegt, benötigen wir die Ober- und Untergrenze.
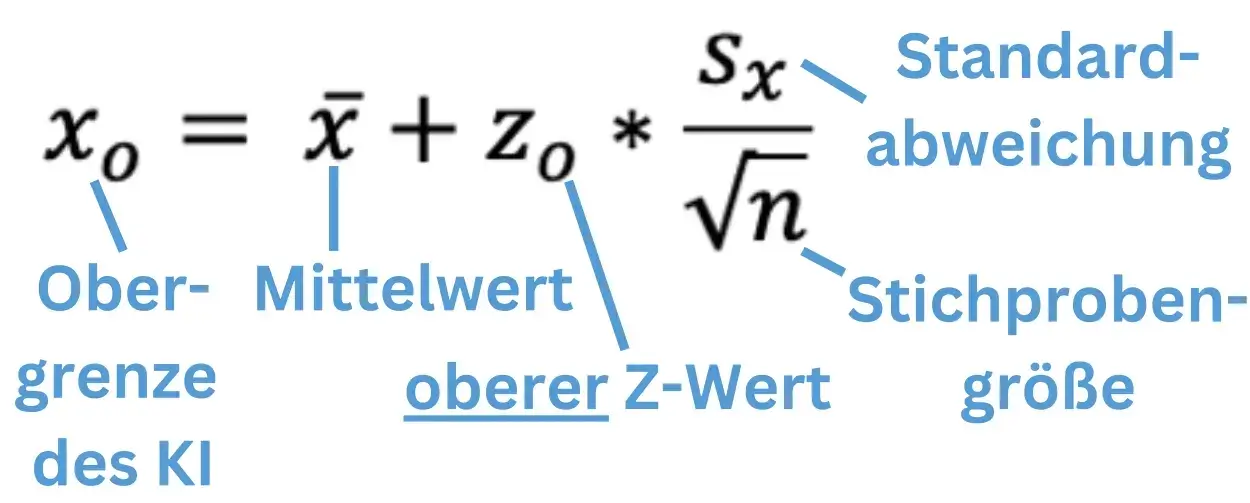
Beginnen wir zunächst mit der Formel der Obergrenze:
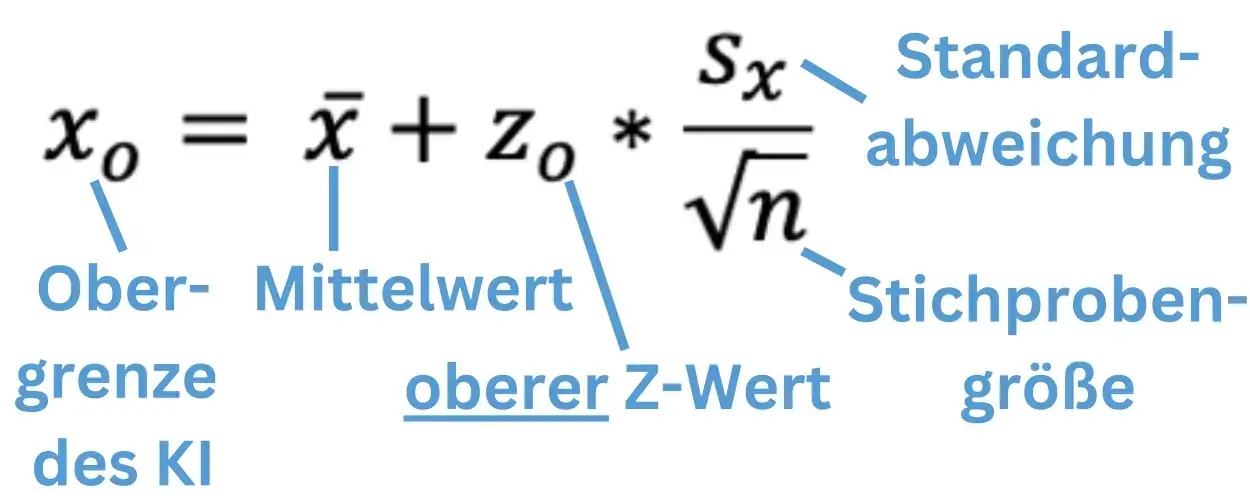
Die meisten Werte findet ihr in Aufgabe oder Z-Tabelle. Die Standardabweichung der Stichprobe müsst ihr aber berechnen, und wie das geht erfahrt ihr im Rechenteil!
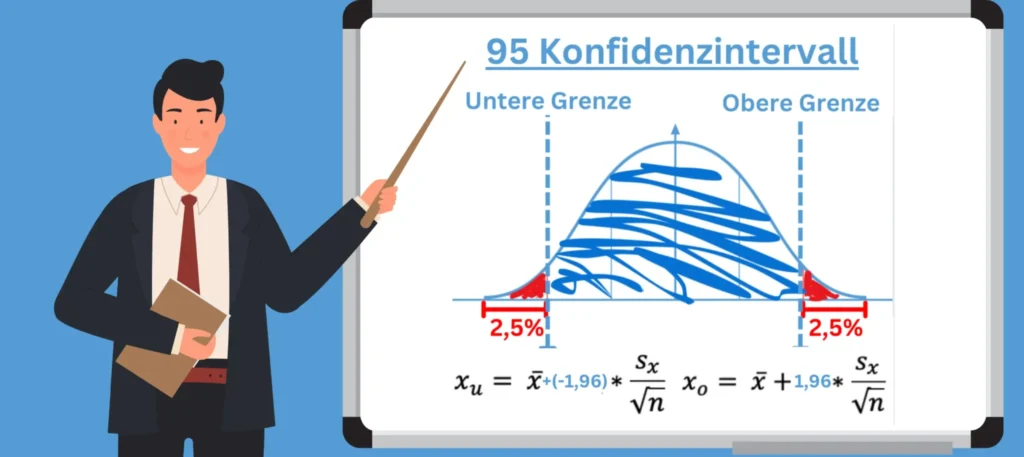
Zo-Wert bei 95 Konfidenzintervall:
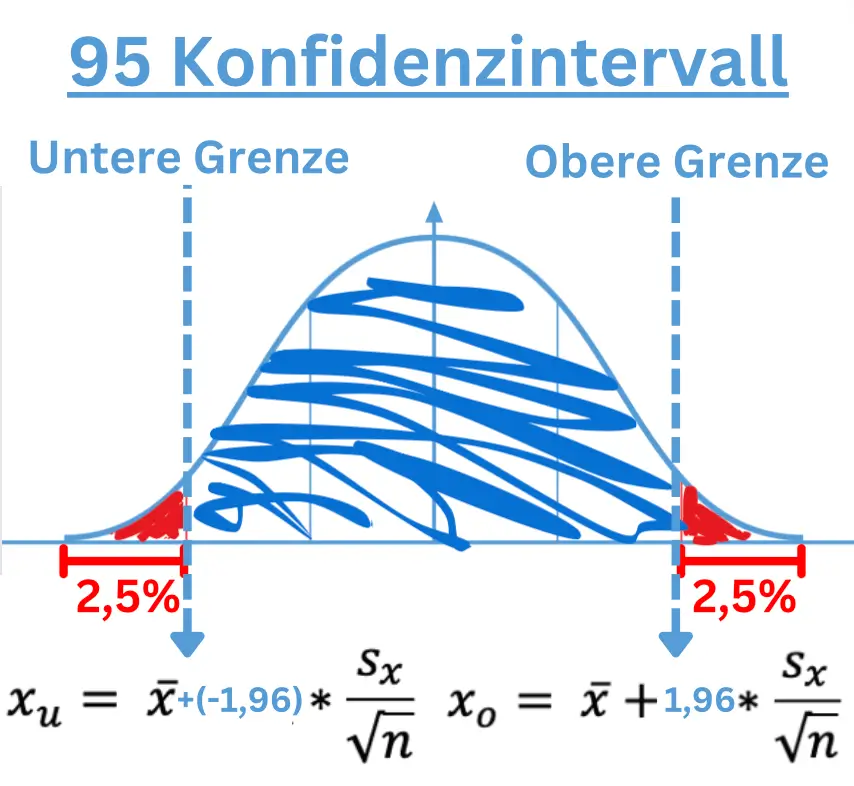
Wir vernachlässigen 5% des KI bei einem 95% Konfidenzintervall!
→ 2,5% oben und 2,5% unten
Damit ist die Obergenze bei 1-0,025 (100% – 2,5%) = 0,975 (=97,5%)
Wir lesen die Z-Tabelle bei 0,975 ab und erhalten Zo-Wert = 1,96.
Häufiger Fehler! Bei einem 95 Konfidenzintervall vernachlässigen wir 5% des Intervalls. Dies verleitet dazu, die Z-Tabelle bei 0,95 abzulesen, dies ist bei einem beidseitigen Test aber falsch! Wir bestimmen die Ober – und Untergrenze (beidseitiger Test) und vernachlässigen damit die oberen 2,5% und unteren 2,5%, was insgesamt 5% sind!
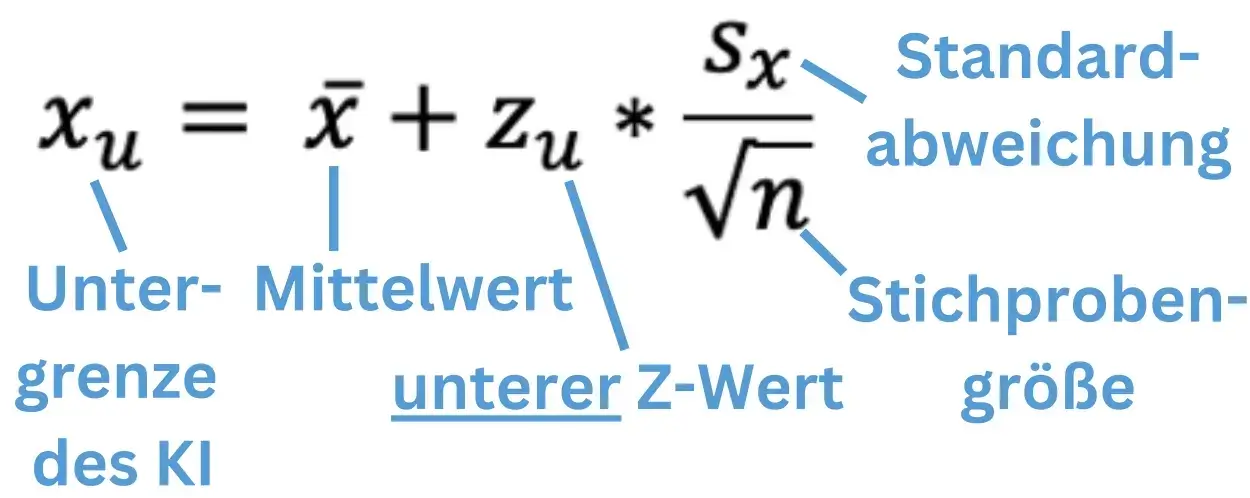
Die Formel der Untergrenze unterscheidet sich nicht wesentlich von der, der Obergrenze!
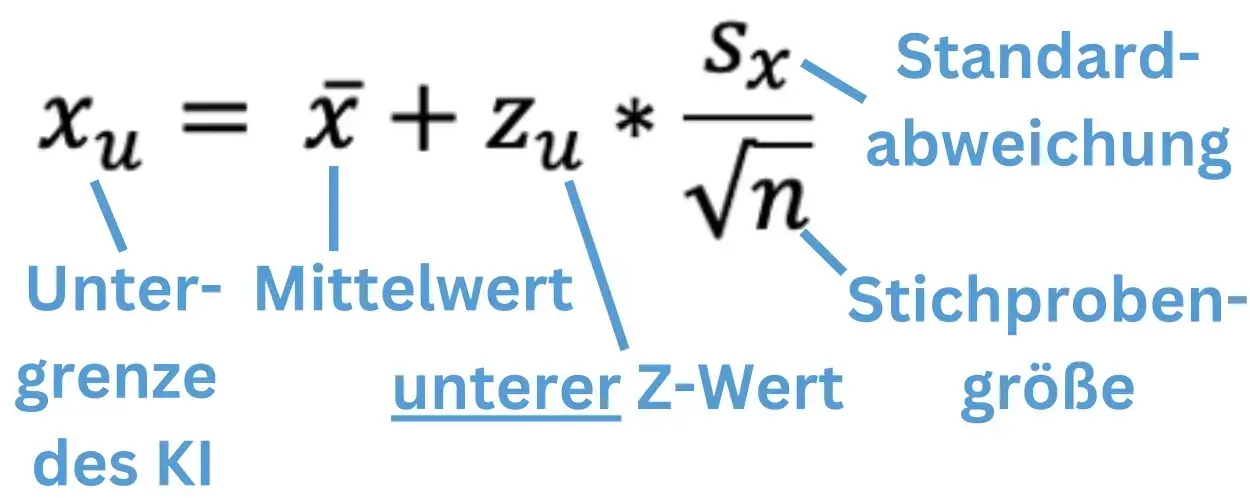
Das Einzige, was sich hier verändert ist logischerweise der Z-Wert! Wir benötigen jetzt den Zu-Wert, da wir die untere Grenze bestimmen wollen.
Zu-Wert bei 95 Konfidenzintervall:
Wir wissen bereits, dass die Obergrenze bei 0,975 liegt und Zo-Wert = 1,96 hat.
Die Untergrenze ist genau auf der gegenüberliegenden Seite der Obergrenze nämlich bei 0,025 (2,5%).
Wir können also einfach das Vorzeichen des Zo-Wertes umdrehen → Zu-Wert = –1,96
T-Verteilung – Formel
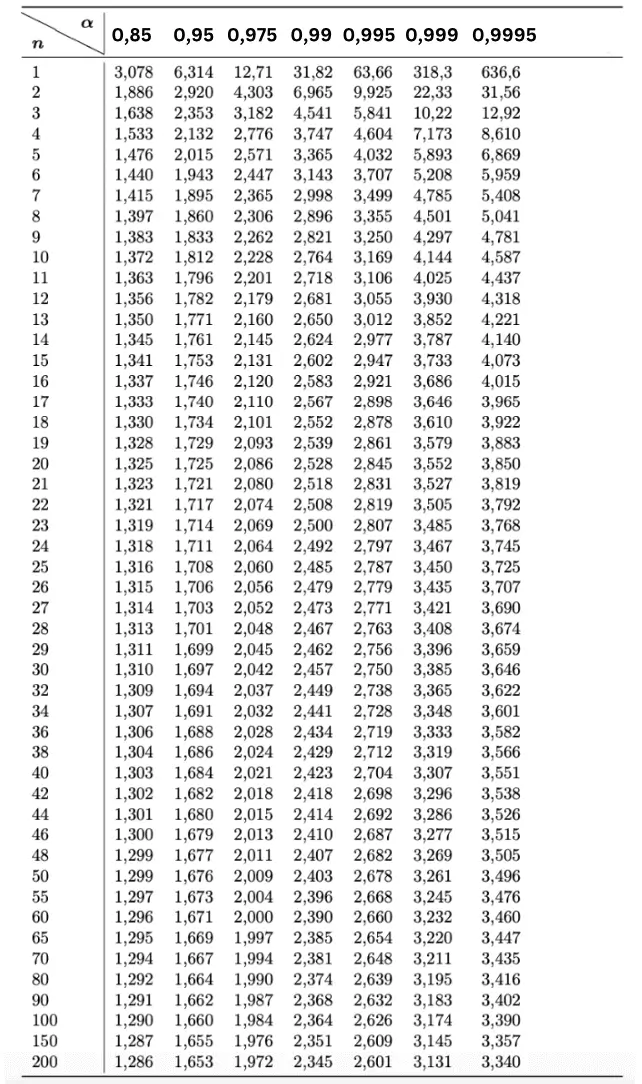
Wissen wir nicht, ob die Grundgesamtheit normalverteilt ist und wenn die Stichprobe nicht sehr groß ist dann benutzen wir die t-Verteilung und lesen die t-Werte in der t-Tabelle für die entsprechenden Freiheitsgrade (n-1) ab.
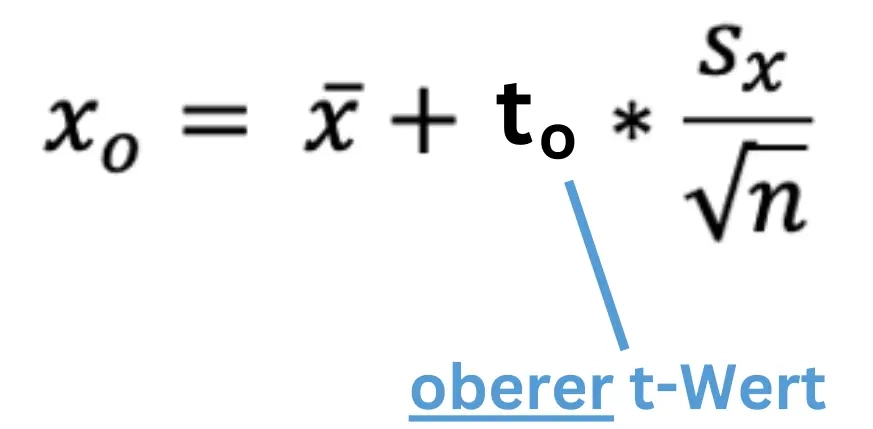
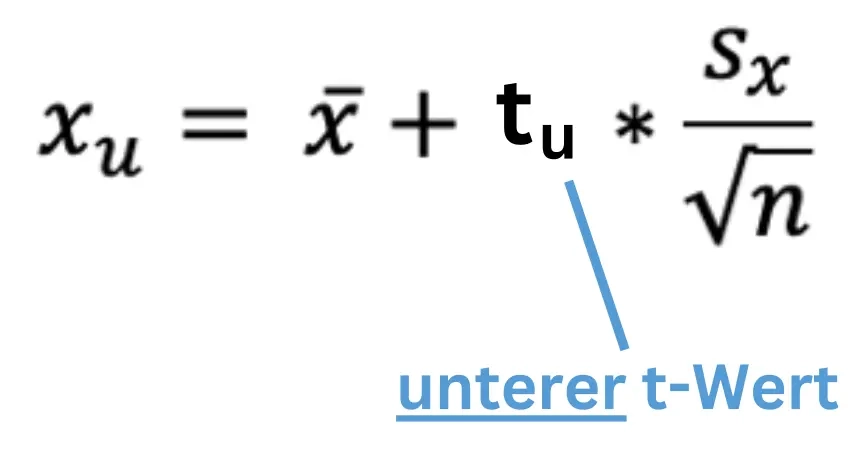
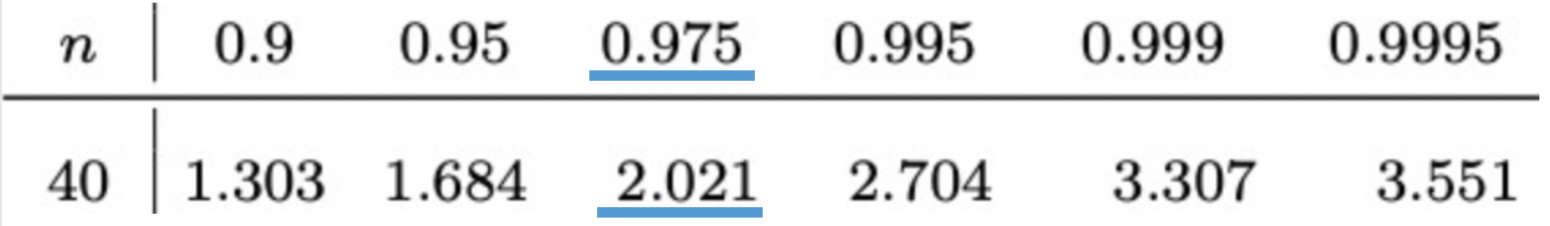
Ein 95% Konfidenzintervall mit 40 Freiheitsgraden (Stichprobengröße n=41) hat einen oberen t-Wert von 2,021 und einen unteren t-Wert von -2,021
Konfidenzintervall 95/99: Definition
Üblicherweise wird in der Statistik gerne ein 95 oder auch 99 Konfidenzintervall benutzt.
Die 95 und die 99 stehen für Kofidenzniveaus. Das heißt die Wahrscheinlichkeit, dass der Bereich des Konfidenzintervalls den wahren Wert beinhaltet. Bei einem 95 KI beträgt diese 95% und bei einem 99 KI 99%.
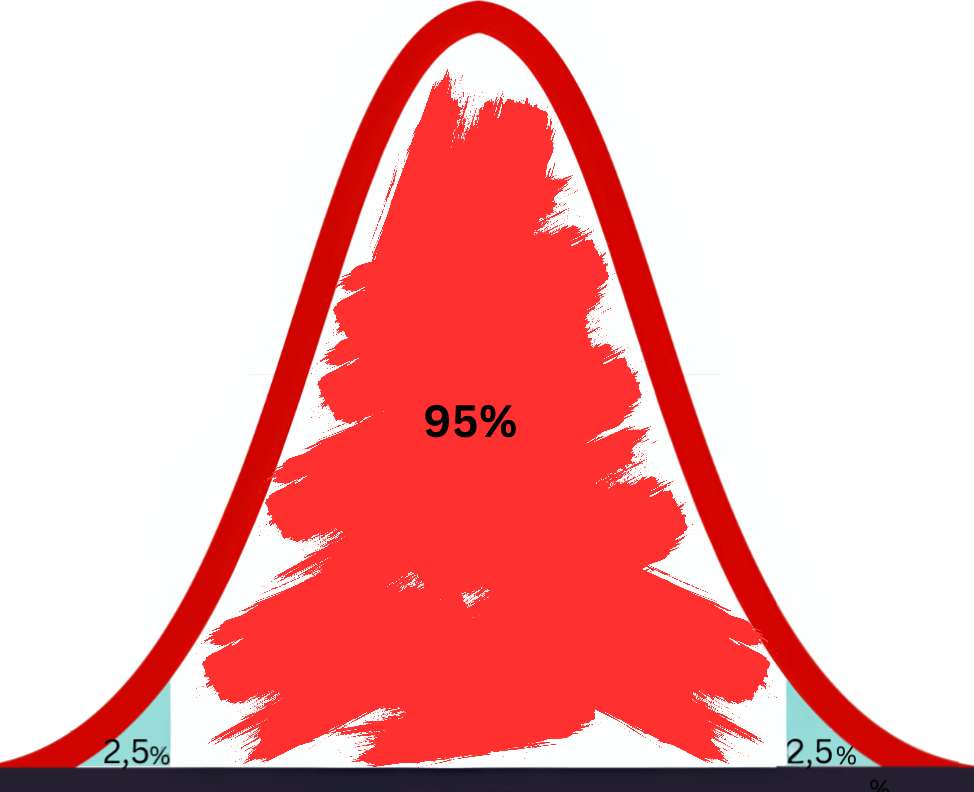
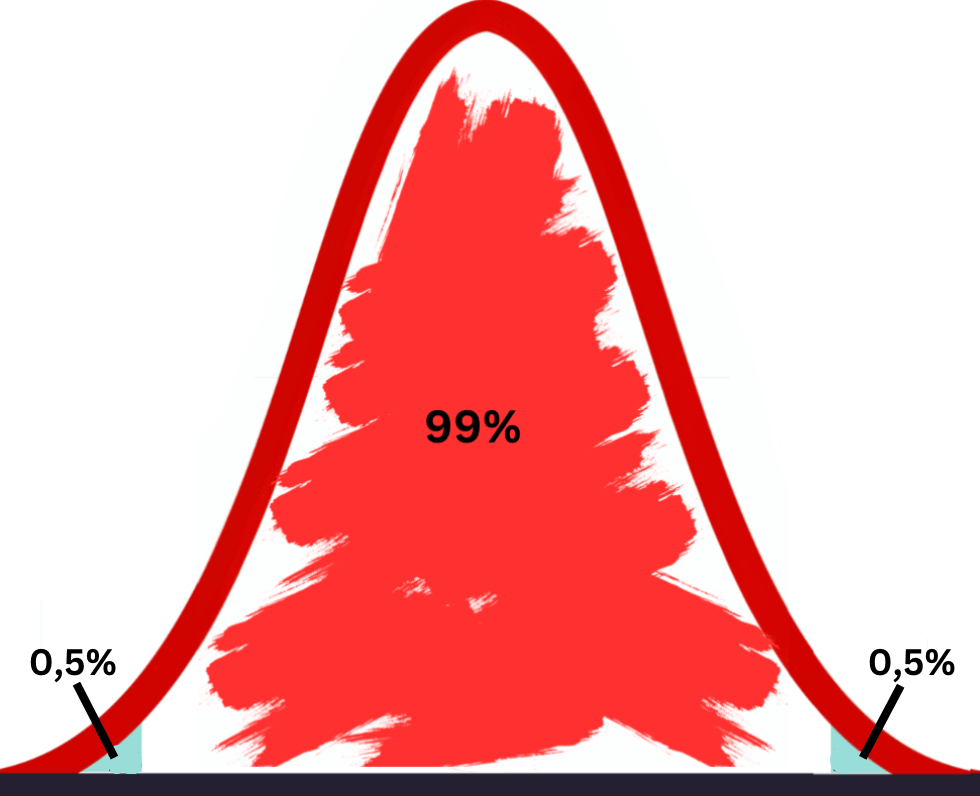
Warum also nicht immer den zuverlässigeren Intervall (99) benutzen?
Zwei Faktoren erhöhen bzw. veringern die Größe unseres Intervalls:
1. Je kleiner die Stichprobengröße → desto größer der Intervall
2. Je höher das Konfidenzniveau → desto größer der Intervall
Wenn wir nur eine kleine Stichprobe haben, und ein hohes Konfidenzniveau (z.B. 99) wählen, dann wird der Intervall sehr groß und wenig aufschlussreich. Es empfiehlt sich der kleinen Stichprobe mit einem niedrigen Konfidenzniveau entgegenzuwirken.
Haben wir eine sehr große Stichprobe, dann können wir natürlich das Konfidenzniveau erhöhen, um unsere Untersuchung noch genauer zu gestalten!
Konfidenzintervall berechnen:
95 KI mit normalverteilter Grundgesamtheit
Aufgabentext:
Du studierst Sport und möchtest eine Uni-Basketballmannschaft gründen. Die Eintrittshürde für ein Uni Team ist eine mittlere Größe von mind. 1,80m. Daher möchtest du die Größe von Teilnehmenden aller Unibasketballkurse herausfinden. Du hast aber wegen der Prüfungsphase nur Zeit für die Größen deines Kurses.
Deine Stichprobe besteht also aus deinem Uni-Basketballkurs von insgesamt 15 Teilnehmern; Die Körpergröße von Menschen ist normalverteilt; Die Teilnehmenden deines Kurses haben die folgenden Größen:
x1=1,90m; x2=1,80m; x3 = 1,77m; x4 = 1,88; x5 = 1,85m; x6=1,92m; x7=1,83m; x8 = 1,79m; x9 = 1,86; x10 = 1,84m; x11 = 1,91m; x12 = 1,83m; x13 = 1,88m; x14 = 1,78m; x15 = 1,85m; Damit ergibt sich eine Durchschnittsgröße von 1,846m ≈ 1,85m.
Aufgabe:
Bestimme den 95 Konfidenzintervall der mittleren Größe von Teilnehmenden aller Basketballkurse. Interpretiere deine Ergebnisse außerdem im Hinblick auf die Eintrittshürde für Uni Teams.
Schritt 1: Was ist gegeben
1. Stichprobengrößen = 15 Teilnehmer deines Basketballkurses
2. Ein Konfidenzniveau von 95 bedeutet Obergrenze bei 97,5% (0,975)
→ Zo -Wert = 1,96
→ für Untergrenze kehren wir das Vorzeichen um: Zu -Wert = -1,96
3. Größen der Teilnehmenden deines Kurses
4. Mittelwert der Stichprobe: x̄ = 1,85m
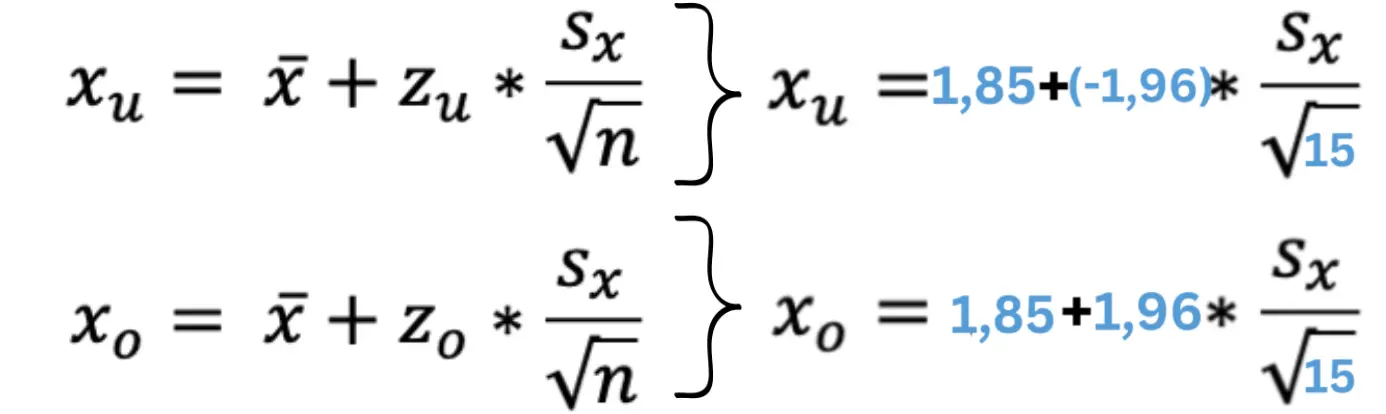
Schritt 2: Was fehlt zum Ergänzen der Formel? →Standardabweichung
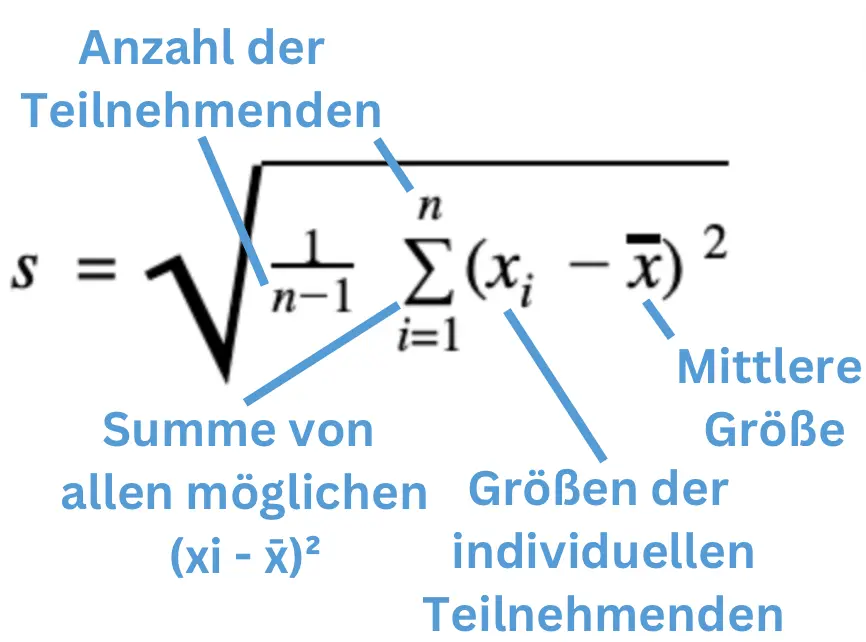
Lass dich hier nicht vom Summenzeichen ∑ verwirren. Das bedeutet einfach, dass wir den Term (xi – x̄)² nach ∑ für alle xi (die individuellen Größen) wiederholen müssen und diese dann zusammenzählen.
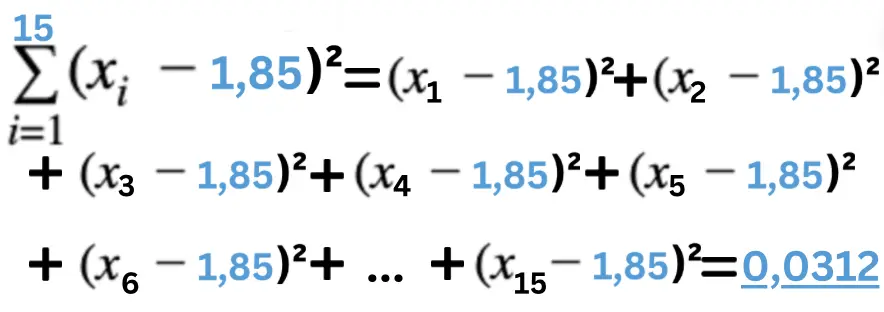
Wir berechnen zuerst das Summenzeichen und dann setzen wir im nächsten Zwischenschritt das Ergebnis des Summenzeichen in die Formel ein. Berechne hierbei immer erst die Terme (xi – x̄)² und addiere dann zum Schluss.
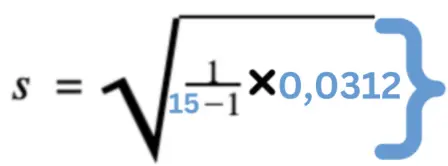
Hier setzen wir das Ergebnis des Summenzeichens in die Formel der Standardabweichung ein!
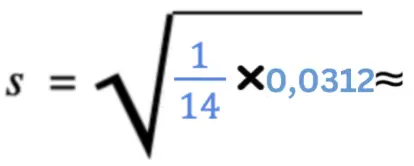
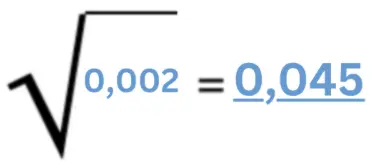
Warum quadrieren wir alle Werte für die Standardabweichung?
Beispiel: x3=1,77m; x̄ = 1,85m → 1,77m – 1,85 = –0,08m
Wir quadrieren, um negative Werte zu vermeiden, später ziehen wir dann die Wurzel, um die Quadrierung aufzuheben.
Schritt 3: Einsetzen aller Werte in die Formel
Da wir nun auch die Standardbweichung haben, können wir diese einfach der Formel hinzufügen und dann im nächsten Schritt einfach ausrechnen.
Häufige Fehlerquellen!
Punkt vor Strich rechnen!
Wir müssen erst den rechten Term der Formel multiplizieren bevor wir diesen mit dem Mittelwert verrechnen können!
Bei der Untergrenze das Minus beachten!
Wir müssen bei der Untergrenze natürlich beim Multiplizieren das negative Vorzeichen von -1,96 beachten
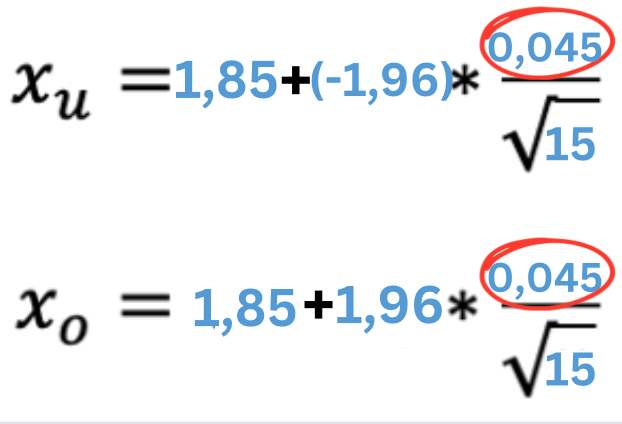
Schritt 4: Ergebnisse festhalten
Die mittlere Größe v0n Teilnehmenden der Basketballkurse befindet sich zu 95% zwischen Xu = 1,83m und Xo = 1,87m
Schritt 5: Interpretation → im nächsten Absatz!
Konfidenzintervall: Interpretation – Rechnung 1
Die Motivation für die Untersuchung war es herauszufinden, wie groß Kursteilnehmende im Schnitt sind, um sicherzustellen, dass ein Uni-Team im Schnitt mind. 1,80m groß und damit erlaubt ist.
Ergeben hat sich, dass die mittlere Größe der Teilnehmenden mit 95%-iger Wahrscheinlichkeit zwischen 1,83m und 1,87m liegt.
Was heißt das nun für unsere Untersuchung?
Der Mindestwert von 1,80m liegt unterhalb unseres Intervalls aber ist das gut? Das ist absolut fantastisch!
Die wahre mittlere Größe muss damit größer als 1,80m sein! Das bedeutet, dass wir mit mindestens 95% Wahrscheinlichkeit kein Problem mit der Eintrittshürde haben!
Um unsere Untersuchung noch genauer zu gestalten, könnten wir nun den 99% Konfidenzintervall aufstellen und danach evtl. den 99.9% Konfidenzintervall. usw. bis wir irgendwann die 1,80m einschließen.
Dann können wir die Stichprobengröße erhöhen, z.B. durch Hinzuzug eines weiteren Kurses. Dies gibt uns die Möglichkeit auch bei hohen Konfidenzniveaus einen kleinen Intervall zu generieren!
Konfidenzintervall berechnen: 99 Konfidenzintervall mit t-verteilter Grundgesamtheit
Nehmen wir nun das Rechenbeispiel der vorherigen Aufgabe – falls du diese nicht angeschaut hast, lies dir schnell den Aufgabentext durch! – und verändern zwei Umstände.
Nimm an, die Körpergröße sei nicht normalverteilt und wir möchten mit einem 99 Konfidenzintervall testen.
Der Richtwert von 1,80m bleibt und die Körpergrößen deines Kurses verändern sich auch nicht!
Aufgabe:
Bestimme den 99 Konfidenzintervall der mittleren Größe von Teilnehmenden aller Basketballkurse. Nimm an, die Körpergröße sei t-verteilt. Interpretiere deine Ergebnisse außerdem im Hinblick auf die Eintrittshürde für Uni Teams.
Schritt 1: Was ist gegeben?
1. Stichprobengrößen = 15 (Teilnehmer deines Basketballkurses)
2. Mittelwert der Stichprobe: x̄ = 1,85m
3. Standardabweichung der Stichprobe: Sx = 0,045
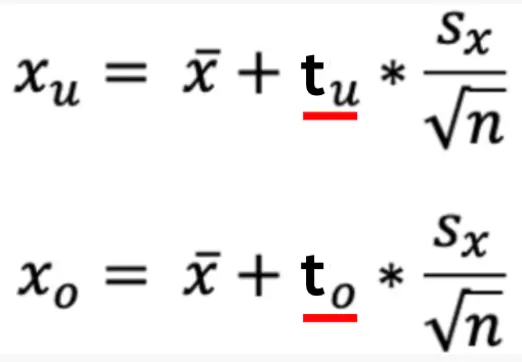
Schritt 2: Was fehlt zum Ergänzen der Formel? →T-Werte
Um T-Werte abzulesen sind zwei Faktoren zu beachten:
1. Wie bei der Normalverteilung das Konfidenzniveau
2. Die Freiheitsgrade
zu 1.: Konfidenzniveau = 99, Wir vernachlässigen 1% insgesamt bzw. 0,5% oben und 0,5% unten. Damit ist die Obergrenze bei 100%-0,5% = 99,5% → Obergrenze: 0,995
zu 2.: Freiheitsgrade = n – 1 = 15 – 1 = 14
→ Wir lesen also bei 0,995 und 14 Freiheitsgraden in der T-Tabelle ab und erhalten: To-Wert = 2,977
→ Für den Tu-Wert drehen wir einfach das Vorzeichen um: Tu-Wert = -2,977
Schritt 3: Einsetzen aller Werte in die Formel
Da wir nun auch die T-Werte haben, können wir diese einfach der Formel hinzufügen und dann im nächsten Schritt einfach ausrechnen.
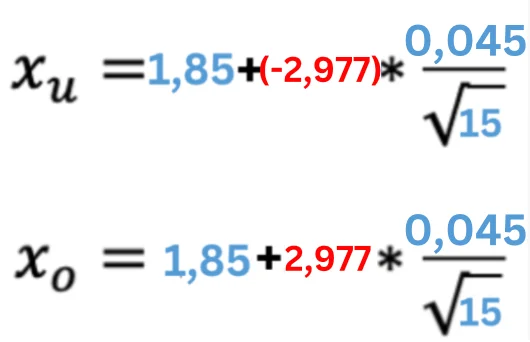
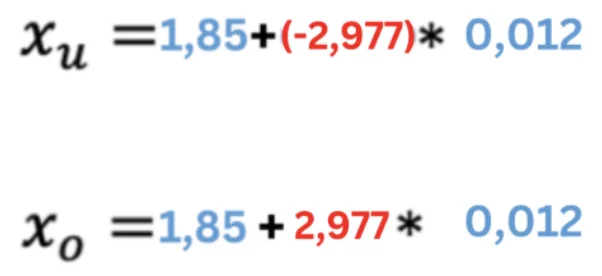
Schritt 4: Ergebnisse festhalten
Die mittlere Größe v0n Teilnehmenden der Basketballkurse befindet sich zu 99% zwischen Xu = 1,70m und Xo = 2,0m
Schritt 5: Interpretation → im nächsten Absatz
Konfidenzintervall: Interpretation – Rechnung 2
Im Vergleich zum vorangegangenen Beispiel hat sich der Intervall wie folgt verändert: Xu: 1,83m → 1,81m auf Xo: 1,87m → 1,89m verschoben.
Diese Entwicklung ist den zwei neuen Umständen geschuldet:
1. Die T-Verteilung hat für niedrige Freiheitsgrade größere Beträge, als die Normalverteilung
→ vgl. To-Wert 99KI = 2,977; Zo-Wert 99KI = 2,576
2.: Das höhere Konfidenzniveau 99 sorgt zudem auch für höhere T-Werte als bei einem 95 Konfidenzniveau
→ vgl. To-Wert 99KI = 2,977; To-Wert 95KI = 2,145
Es ist bei T-Verteilten Grundgesamtheiten und wenn wir mit hohen Konfidenzniveaus arbeiten wollen noch wichtiger eine große Stichprobe zu haben!
Der wahre Mittelwert ist auch bei T-Verteilung und höherem Konfidenzniveau noch unterhalb unseres Intervalls. Ein weiteres gutes Zeichen für dein Basketballteam!
Konfidenzintervall: Weitere Übungen
Zum überprüfen deiner Ergebnisse für Mittelwert und Standardabweichung empfehlen wir dir diesen Rechner!
Und für alle weiteren Kalkulationen jenen Rechner!
1. Folgeaufgabe: Die Eintrittshürde hat sich nun auf 1,85m erhöht
→ Da der Intervall diese Größe mit einschließt ist nicht mehr sicher, dass ein Team im Schnitt mind. 1,85m groß ist wir brauchen mehr Daten, um sicher sein zu können, dass wir die neue Hürde überschreiten.
Deshalb möchtest du deine vorherige Untersuchung genauer gestalten und bittest einen Freund dir die Größen seines Kurses zu senden:
x16 = 1,85; x17 = 1,76; x18 = 1,95; x19 = 1,76; x20 = 1,83; x21 =1,84; x22 = 1,93; x23 = 1,67; x24 = 1,70; x25 = 2,00; x26 = 1,75; x27 = 1,68; x28 =1,78 x29 = 1,64; x30 = 1,69;
Mittelwert von deinen ursprünglichen 15 Teilnehmern: x̄ = 1,85m
x1=1,90m; x2=1,80m; x3 = 1,77m; x4 = 1,88; x5 = 1,85m; x6=1,92m; x7=1,83m; x8 = 1,79m; x9 = 1,86; x10 = 1,84m; x11 = 1,91m; x12 = 1,83m; x13 = 1,88m; x14 = 1,78m; x15 = 1,85m
Aufgabe:
Bestimme den neuen Mittelwert deiner Stichprobe und stelle danach erneut den 95% Konfidenzintervall auf. Nimm an, dass die Körpergrößen normalverteilt sind. Interpretiere deine Ergebnisse.
2. Briefe von Campteilnehmern
Der Leiter eines Ferienlagers interessiert sich für die durchschnittliche Anzahl der Briefe, die jedes Kind während seines Aufenthaltes im Ferienlager verschickt.
Die Grundgesamtheit ist normalverteilt. Es wird eine Umfrage unter 20 Campteilnehmern durchgeführt. Der Mittelwert der Stichprobe beträgt 7,9 mit einer Standardabweichung von 2,8.
Aufgabe:
Konstruiere einen 90%-Konfidenzintervall für den Mittelwert der Anzahl der Briefe, die die Camper nach Hause schicken.
1. Folgeaufgabe
x̄ = 1,82; Sx = 0,086; Xu = 1,79; Xo = 1,85
Interpretation: Die Eintrittshürde von 1,85m wird von unserem Intervalls zwar eingeschlossen, aber es ist dennoch unwahrscheinlich, dass ein zufälliges Team der Basketballkurse die Hürde überschreiten würde.
Mögliche Erklärung für den größeren Intervall hier, trotz größerer Stichprobe: Pech! Die zweite Stichprobe könnte auch einfach voll von Ausreißern sein. Es gilt weiterhin: Stichprobengröße erhöhen, um unsere Chancen auf gute Ergebnisse zu vergrößern.
2. Briefe der Campteilnehmer
Stichprobenparameter:
n = 20; x̄ = 7,9; Sx = 2,5
Konfidenzintervall:
Xu = 6,98; Xo = 8,82