Du suchst Informationen zum Kommutativgesetz und willst lernen, wie du richtig vertauschen kannst? Dann bist du hier goldrichtig!
In diesem Artikel erfährst du…
… was das Kommutativgesetz ist
… wann du es anwenden kannst
… und wie du damit rechnen kannst
Außerdem warten am Ende vom Artikel noch hilfreiche Übungsaufgaben für dich.
Lass uns direkt anfangen…
Kommutativgesetz – wie lautet es?
a+b = b+a
a•b = b•a
Was bringt das Kommutativgesetz?
Das Kommutativgesetz der Addition besagt, dass die Summanden einer Plus-Rechnung beliebig vertauscht werden dürfen.

Das Kommutativgesetz der Multiplikation besagt, dass die Faktoren einer Mal-Rechnung beliebig vertauscht werden dürfen.
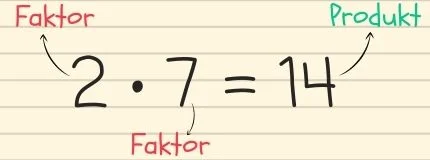
Es ist also egal ob du 5•3 rechnest oder 3•5. Du kommst in beiden Fällen auf 15.
Vertauschungsgesetz – Beispiele mit Beweisen
6+4 = 4+6
10 = 10
1+24+6+8 = 24+8+1+6
39 = 39
7•3 = 3•7
21 = 21
5•2•9 = 2•9•5
90 = 90
Bei all diesen Beispielen sind beide Seiten der Additionen und Multiplikationen gleich, egal in welcher Reihenfolge gerechnet wird.
Kommutativgesetz, Assoziativgesetz, Distributivgesetz – was ist der Unterschied?
Im Folgenden erklären wir dir kurz die drei wichtigsten Gesetze in der Algebra.
Was sind die drei Mathe Gesetze?
Kommutativgesetz, Assoziativgesetz und Distributivgesetz.
Kommutativgesetz:
a+b = b+a; a•b = b•a
Assoziativgesetz:
a+(b+c) = (a+b)+c; a•(b•c) = (a•b)•c
Distributivgesetz:
a•(b+c) = a•b+a•c; a•(b-c) = a•b-a•c
Kommutativgesetz und Assoziativgesetz – was ist der Unterschied?
Das Assoziativgesetz besagt, dass bei einer reinen Addition oder Multiplikation die Klammer/n beliebig verschoben werden können, ohne damit das Ergebnis zu verändern.
Beim Kommutativgesetz geht es wie oben erklärt darum, dass man die Teile einer Rechnung miteinander vertauschen kann, während sich das Ergebnis nicht ändert.
Der Unterschied liegt also darin, dass beim Assoziativgesetz Klammern den Platz wechseln und beim Kommutativgesetz einzelne Terme der Rechnung.
Das Assoziativgesetz und das Kommutativgesetz haben gemeinsam, dass sie beide nur bei Additionen und Multiplikationen anwendbar sind.
Für welche Rechenarten gilt das Kommutativgesetz?
Das Kommutativgesetz gilt für Additionen und Multiplikationen. Also wenn du plus oder mal rechnest.
Beim Assoziativgesetz ist das genauso.
Kommutativgesetz bei der Addition
Bei Additionen ist es egal, in welcher Reihenfolge du eine Rechnung durchführst. Du wirst immer beim gleichen Ergebnis landen. Es ist dabei egal wie viele Zahlen du addierst.
4+7+1+3+9+15+6 = 6+9+1+3+7+15+4
45 = 45
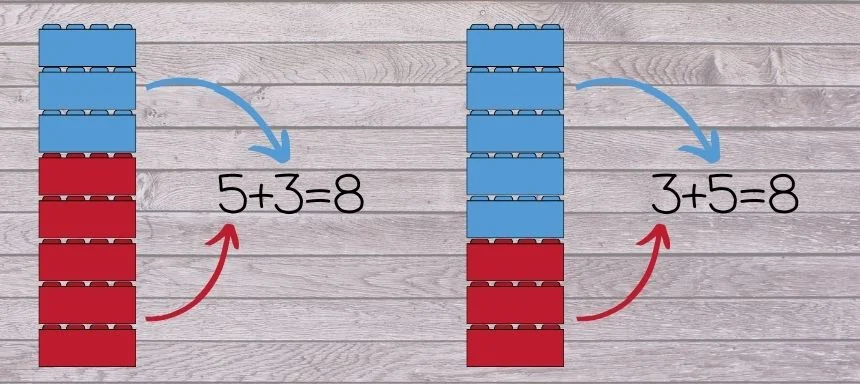
In diesem Bild siehst du, dass es egal ist, ob du 5+3 oder 3+5 Klötze rechnest. Beide Türme sind 8 Klötze hoch.
Mit dem Kommutativgesetz multiplizieren
Neben der Addition kannst du das Kommutativgesetz auch bei der Multiplikation anwenden.
Hier ist es ebenfalls egal, wo welche Zahl steht.
Auch hier ist die Menge der Zahlen unwichtig.
8•5 = 5•8
40 = 40
5•3•4•10 = 4•3•10•5
600 = 600
Hier siehst du, dass es keinen Unterschied macht, ob du 3•2 oder 2•3 Steine rechnest. Das Ergebnis ist immer 6 Steine.

Du hast Fragen zum Addieren von Brüchen? Wir haben Antworten!
Subtraktion und Division – hier bitte nicht vertauschen
Bei Subtraktionen (-) und Divisionen (:) darfst du das Kommutativgesetz nicht anwenden. Wir zeigen dir auch warum.
Vertauschen bei Subtraktion und Division führt zu unterschiedlichen Ergebnissen
6-2 ≠ 2-6
4 ≠ -4
Wie du siehst sind die beiden Seiten nicht gleich.
Stell dir vor, du hast 6 Stück Kuchen und isst 2 davon. Wie viele bleiben übrig? Genau, 4 Stück.
Hast du am Anfang 2 Stück und willst 6 essen, gibt es ein Problem. Hier bleiben nicht 4 Stück übrig.
Du erhältst also nicht das gleiche Ergebnis wenn du 6-2 und 2-6 rechnest.
Auch beim Dividieren ist das Kommutativgesetz nicht anwendbar.
10:5 ≠ 5:10
2 ≠ 0,5
Es macht also einen Unterschied in welcher Reihenfolge du die Rechnung durchführst.
Stell dir hier gerne wieder Kuchen vor. Wenn du 10 Kuchen hast und sie durch 5 Personen teilst, bekommt jeder zwei ganze Kuchen.
Hast du aber 5 Kuchen und willst sie unter 10 Personen aufteilen, erhält jeder nur einen halben Kuchen.
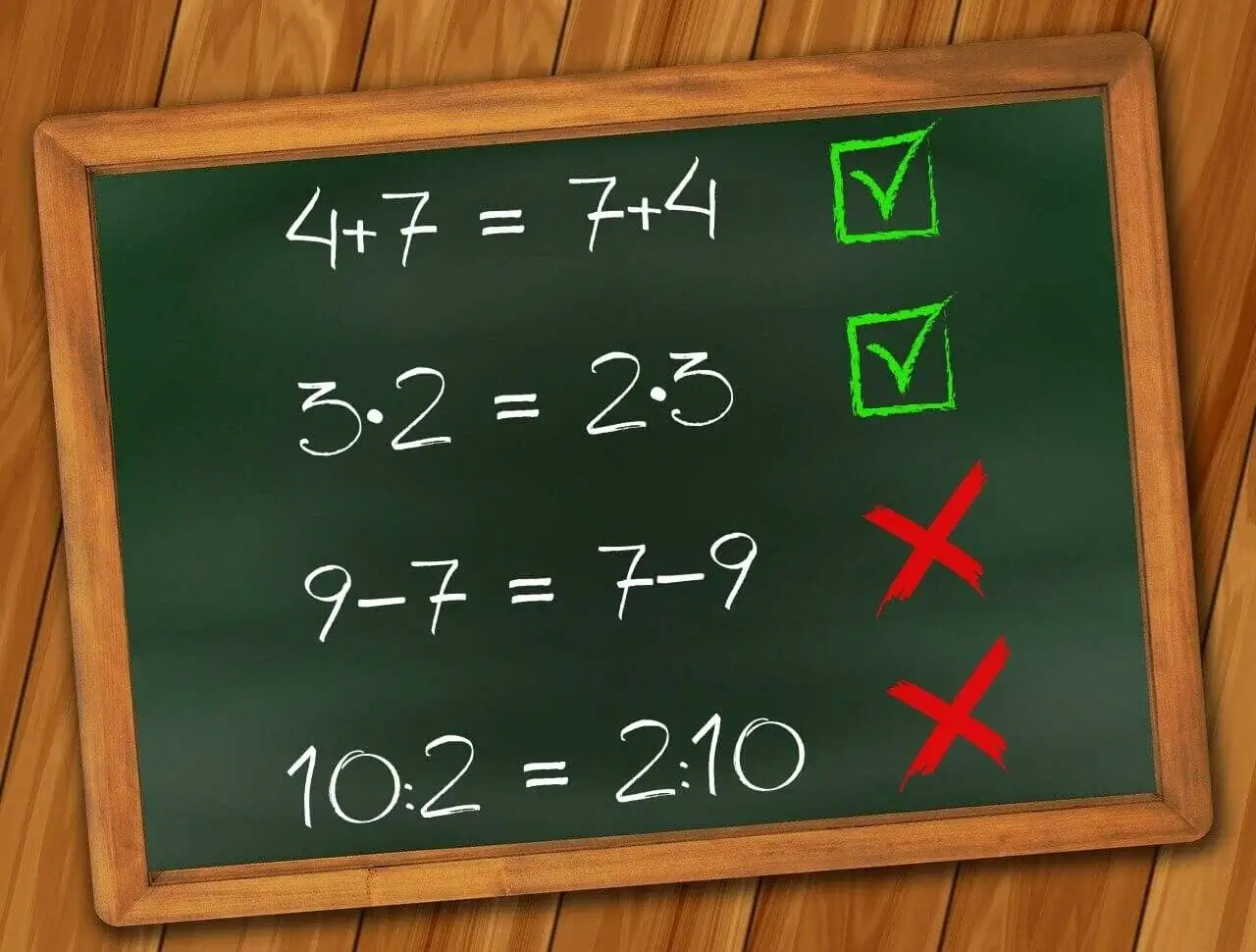
Fazit: Wie du siehst, ist das Kommutativgesetz gar nicht schwer. Wir hoffen, wir konnten dir alle Fragen beantworten und freuen uns immer über Kommentare. Hier haben wir dir noch einen Spickzettel geschrieben mit allen wichtigen Infos übers Kommutativgesetz.

Unseren Spickzettel kannst du hier auch gerne für dich runterladen.
Kommutativgesetz Übungen mit Lösungen
Überlege, ob die folgenden Gleichungen stimmen d.h. ob beide Seiten gleich sind und das Kommutativgesetz angewendet werden kann. Klicke dann einfach auf die Aufgabe, um die Lösung anzuzeigen.
Richtig, da es sich um eine Addition handelt.
Falsch, da es eine Division ist.
Falsch, weil es eine Subtraktion ist.
Richtig, weil es eine Multiplikation ist.
Richtig, hier wird addiert. 5 ist der eine Summand, (3-1) der zweite.
Falsch, das ist eine Subtraktion. Man kann nicht (2•6) und 8 vertauschen.
Richtig, weil hier plus gerechnet wird.
Falsch, hier wird dividiert. 10 und (6+2) können nicht vertauscht werden.
Noch Mathe Nachhilfe gesucht? Wir bieten beim Nachhilfe-Team Matheunterricht direkt bei dir Zuhause oder sogar Online an.
Stelle uns direkt eine unverbindliche Anfrage und finde bei uns einen zu dir passenden Tutor!
Hier kommst du zu unseren Artikeln zum Berechnen von Geschwindigkeit, zu den Asymptoten und zur Integralrechnung.
