4,20 von 5 Sterne
Loading...
Im Matheunterricht ist gerade das Thema Kegel mit Volumen, Mantelfläche und Oberfläche berechnen an der Reihe und du bist dir unsicher, wie das geht?
Hier bist du genau richtig, denn wir erklären dir Schritt für Schritt, was ein Kegel ist und wie du seine Flächen berechnest. Teste zum Schluss dein Wissen und löse unsere Übungsfragen!
Schrägbild Kegel
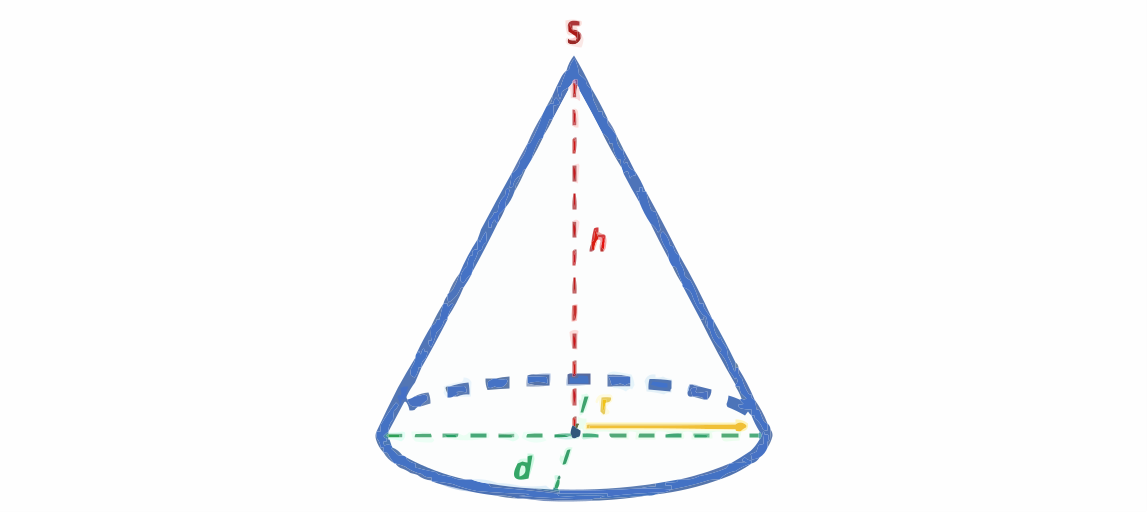
Eigenschaften
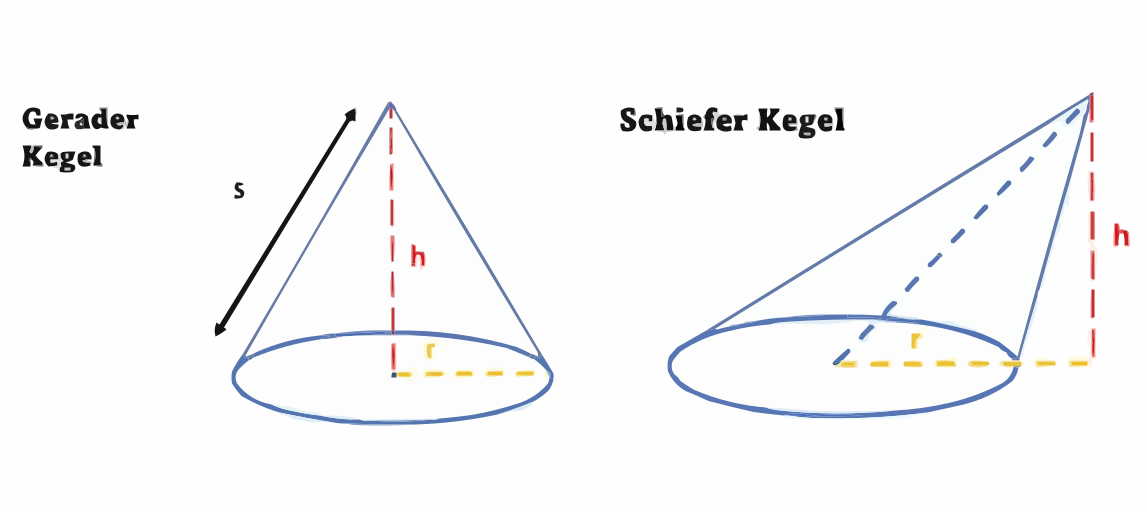
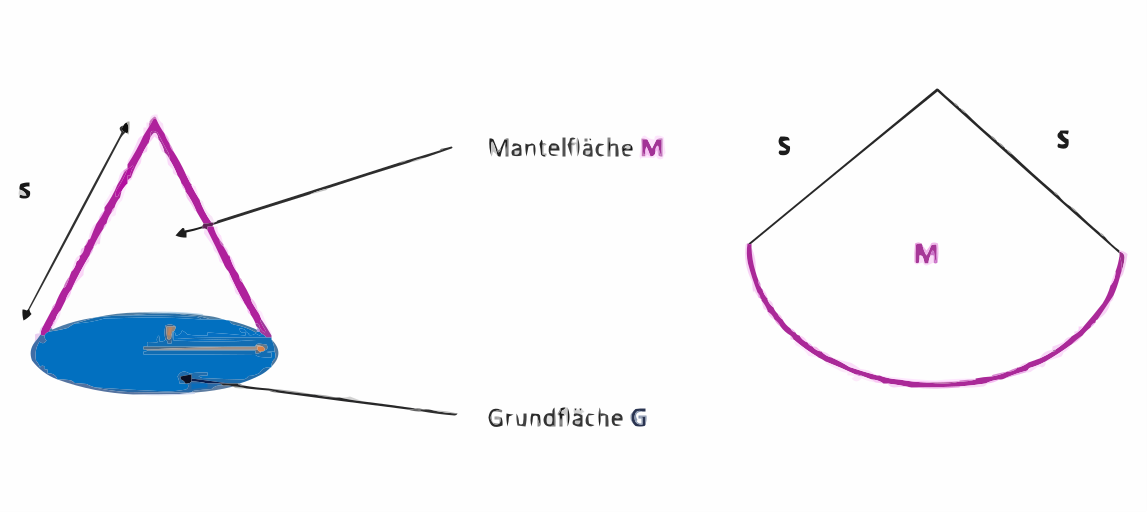
Es gibt gerade und schiefe Kegel. Ein gerader hat gleich lange Mantellinien s. Eine solche Linie ist die kürzeste Verbindung der Kreislinie der Grundfläche zur Spitze. Der Mantel ist ein Kreisausschnitt und wird auch Mantelfläche M genannt. Alle anderen sind schiefe Kegel.
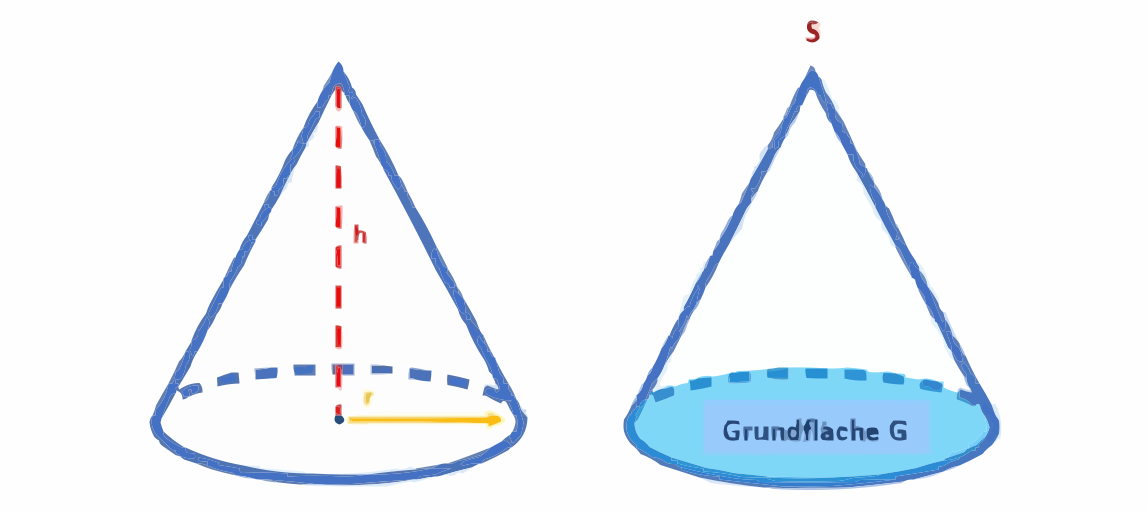
Kreiskegel
Hat ein Kegel einen Kreis als Grundfläche G, wird er Kreiskegel genannt. Dieser verbindet alle Punkte eines Kreises mit einem Punkt, der außerhalb der Kreisebene liegt. Gerade Kreiskegel haben eine Spitze S. Sie befindet sich senkrecht über dem Mittelpunkt der Grundfläche.
Kegel berechnen
Bei einem solchen Körper kann man Volumen, Mantelfläche und Oberfläche ausrechnen. Wir erklären dir im Folgenden anhand von Beispielen, wie du sie Schritt für Schritt berechnest und was ein Kegelstumpf ist.
Volumen Kegel
Den räumlichen Inhalt eines Körpers bezeichnet man als Volumen.
Bei einem Kegel wird es mit dem Radius r und der Höhe h berechnet. Die Volumen Formel lautet:
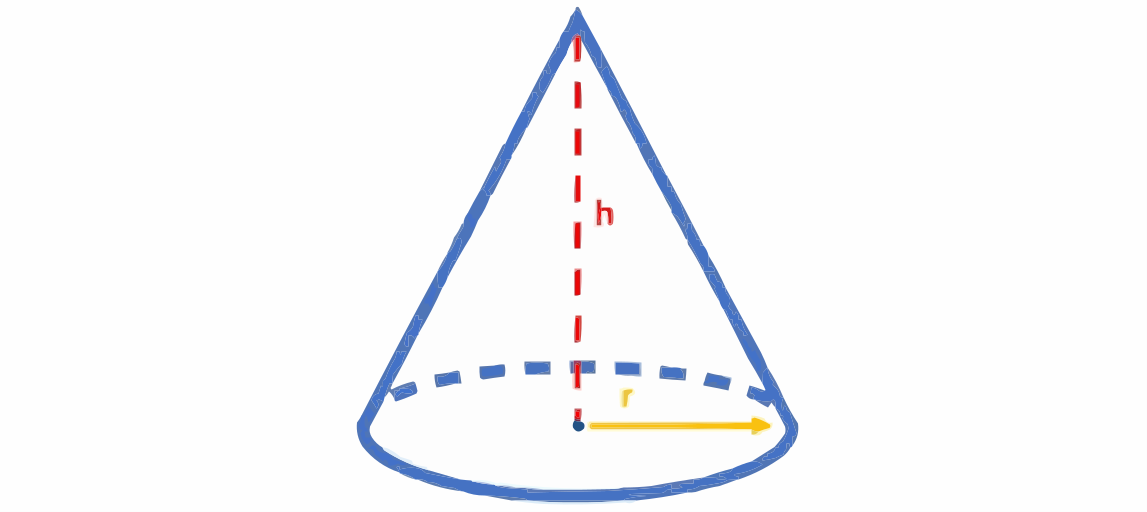
Übung: Berechne das Volumen mit dem Radius r = 12 cm und der Höhe h = 28 cm.
Das Volumen beträgt 4.222,30 cm³.
Mantelfläche Kegel
Die Mantelfläche M besteht aus dem Kreisausschnitt, der ausgehend von der Grundfläche zur Spitze führt.
Möchtest du die Mantelfläche berechnen, musst du folgende Formel benutzen:
Die Mantelfläche beim Kegel ist die Oberfläche ohne Grund- und Deckfläche!
Ist die Mantellinie s nicht gegeben, kannst du sie leicht mit dem Satz des Pythagoras berechnen! Nutze hierfür die Kegelhöhe h und den Radius r.
Übung: Wie groß ist die Mantelfläche mit dem Radius r = 12 cm und der Mantelhöhe s = 26 cm?
Die Mantelfläche beträgt 980,18 cm².
Oberfläche Kegel
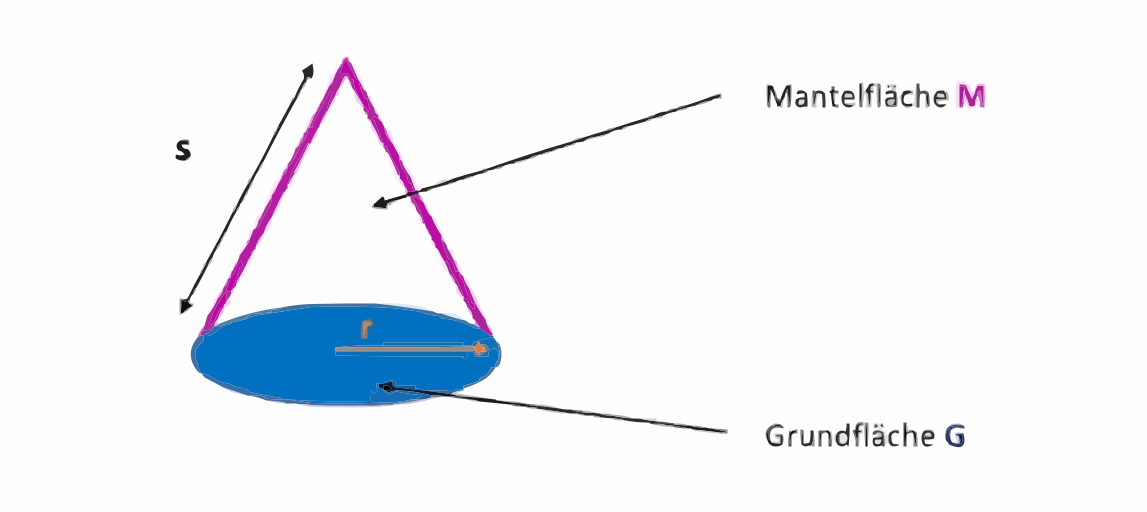
Der Oberflächeninhalt setzt sich aus der Mantelfläche und der Grundfläche zusammen. Er lässt sich einfach ausrechnen, indem du die Grundfläche G mit der Mantelfläche M addierst:
Übung: Wie groß ist der Oberflächeninhalt mit den Maßen r = 12 cm und s = 26 cm?
Der Oberflächeninhalt beträgt 1432,57 cm².
Kegelstumpf
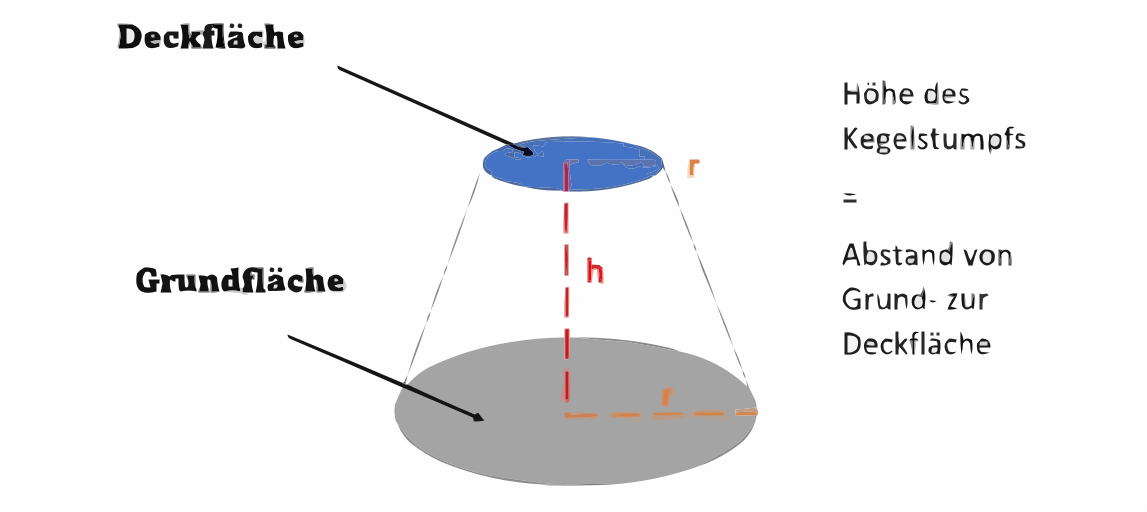
Wenn du von einem geraden Kreiskegel die Spitze abschneidest, erhälst du einen sogenannten Kegelstumpf. Er ist ein Rotationskörper, der auch eine Grundfläche und eine Mantelfläche hat. Zusätzlich besitzt er noch eine kleinere Deckfläche.
Wusstest du, dass der Kegelstumpf im Alltag einfach ein Eimer, ein Glas oder ein Baukegel sein kann?
Jetzt bist du gut auf den Unterricht vorbereitet. Als kleine Übung kannst du gerne die folgenden Fragen beantworten, um dich selbst zu testen.
FAQ
1. Was ist ein Kegel?
Ein Kegel ist in der Geometrie ein dreidimensionaler Körper. Er hat eine Grundfläche und eine Mantelfläche. Generell wird zwischen geraden und schiefen Kegeln unterschieden.
2. Was bedeutet M im Kegel?
Das Kürzel M steht für die Mantelfläche, die mit der Grundfläche des Kegels verbunden ist. Sie ist von Mantellinien eingerahmt, die zu einer Spitze verlaufen.
3. Wie viele Flächen hat ein Kegel?
Ein Kegel hat zwei Flächen: Die Grundfläche und die Mantelfläche.
4. Wie viele Ecken hat ein Kegel?
Ein Kegel hat eine Ecke, nämlich die Spitze. Außerdem gibt es noch zwei Flächen (Grund- und Mantelfläche) und eine Kante (Kreislinie).
5. Was ist ein Kegelstumpf?
Ein Kegelstumpf ist ein Rotationskörper. Er hat die Form eines Kegels, an dem die Spitze abgeschnitten wurde. Ein solcher Stumpf hat eine Grund- und Mantelfläche. Außerdem besitzt er eine Deckfläche.
Schau dir zusätzlich unsere Artikel zum Thema Kreis berechnen und Kugel berechnen an.
Wir stehen für Fragen und Anregungen immer zur Verfügung und freuen uns, wenn wir dir helfen können!
Lass uns gerne einen Kommentar mit deiner Meinung zum Artikel da, wir würden uns sehr freuen!
4,20 von 5 Sterne
Loading...
