4,40 von 5 Sterne
Loading...
Du behandelst das Thema Geraden momentan in der Schule, dein Lehrer erklärt es kompliziert und du hast gerade Panik? Keine Sorge! Lass mich dir helfen und du wirst sehen, dass es gar nicht so schwer ist.
Bereit? Na, dann los!
Was ist eine Gerade?
Eine Gerade, auch als Lineare Funktion bekannt, ist ein Graph im Koordinatensystem. Eine Gerade ist unendlich lang, hat also keinen Anfang und kein Ende und ist – wie vielleicht schon erwartet – gerade.
Geradengleichung
Die Geradengleichung (= allgemeine lineare Funktionsgleichung) wird so dargestellt:
y = m*x + b
Das m ist hier die Steigung der Geraden und b ist der y-Achsenabschnitt. Wichtig zu erwähnen ist, ist dass ein Punkt einer Geraden so dargestellt wird: P (x/y). Die x-Koordinate wird auch Abszisse und die y-Koordinate Ordinate genannt.
Geraden bestimmen – durch Ablesen
Du kannst die Geraden von dem Koordinatensystem auch ablesen, falls man diese ablesen kann. ?
Ich fange immer mit dem y-Achsenabschnitt an. Ich schaue, wo die Gerade die y-Achse schneidet und bestimme das b.
Als nächstes kommt die Steigung. Hier schaust du nach einem sogenannten Steigungsdreieck. Ausgangspunkt ist hier am besten der y-Achsenabschnitt. Du zählst wie viele Kästchen es nach links und viele Kästchen es nach oben sind bis du auf einen gut lesbaren Punkt stößt. Und so bildest du einen Bruch: Das Kästchen nach oben ist der Zähler und das Kästchen nach links ist der Nenner.
Das Bilden eines Bruches kann dir das wiederum beim Einzeichnen einer Geraden helfen.
Beispiel A
Du suchst als Erstes die Schnittstelle mit der y-Achse und bestimmst somit b. –> b = 1
Jetzt suchst du dir einen gut lesbaren Punkt auf der Geraden und bildest ein Steigungsdreieck um m zu bestimmen. –> eins nach links, zwei hoch 2/1 –> m= 2
y = 2x + 1
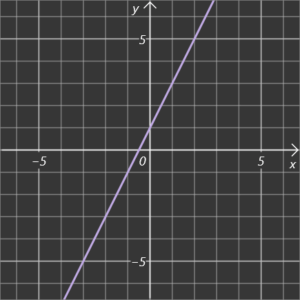
Beispiel B
Auch hier suchst du als Erstes die Schnittstelle mit der y-Achse und bestimmst somit b. Hier geht die Gerade durch den Ursprung, das heißt b = 0
Jetzt suchst du dir einen gut lesbaren Punkt auf der Geraden und bildest ein Steigungsdreieck um m zu bestimmen. –> zwei nach links, eins hoch 1/2. Hier fällt die Gerade. Das heißt, wir haben eine negative Steigung –> m=- 1/( 2)
y = -1/2x
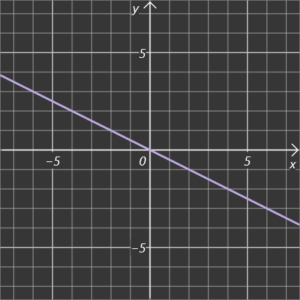
Beispiel C
Wie auch bei den Beispielen davor suchst du die Schnittstelle mit der y-Achse und bestimmst somit b. Die Abstände sind hier in 0,2 Schritten. Die Schnittstelle ist kleiner als 0, somit auch negativ –> b = – 1,5 –> – 3/2
Jetzt suchst du dir einen gut lesbaren Punkt auf der Geraden und bildest ein Steigungsdreieck um m zu bestimmen. –> zwei nach links, eins hoch 1/2 . Auch hier fällt die Gerade. Das heißt wir haben auch hier eine negative Steigung –> m= – 1/2
y = -1/2x – 3/2
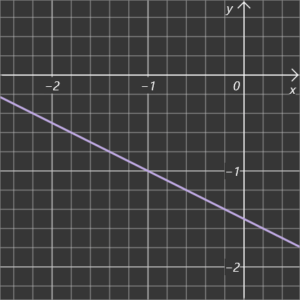
Geraden bestimmen – durch Rechnen
Fern vom Ablesen, kannst du auch Geradengleichungen durch verschiedene Vorgaben bestimmen. Je nach Vorgaben ist die Aufstellung einer Geradengleichung leichter oder schwieriger. Folgst du den Schritten und meinen Tipps, garantiere ich dir, dass du jede Klassenarbeit bestehen kannst.
Geradengleichung bestimmen durch zwei Punkte
Wenn du zwei Punkte, die auf der Geraden liegen gegeben hast, kannst du die Geradengleichung aufstellen. Es gibt 3 Schritte zu Befolgen.
- Steigung berechnen mit der Punkt-Steigungsformel
- Steigung und einen von den zwei Punkten in die allg. Geradengleichung geben
- Ausrechnen und du erhältst den y-Achsenabschnitt b
Dann musst du nur noch alle deine Komponenten (m und b) nehmen und in die allg. Gleichung geben. Und schon kannst du deine Geradengleichung aufstellen.
Natürlich zeige ich dir an einem Beispiel wie das alles funktioniert:
Beispiel: 2 Punkte – P (- 2 / 3) und Q (1 / -1)
1. Setzte die zwei Punkte in die Punkt-Steigungsformel ein
m = (y2 – y1) / (x2 -x1)
m = (- 1 – 3) / (1 – (-2))
m = – 4
2. + 3. m und ein Punkt in die allg. Geradengleichung einsetzten – m = – 4/3 und Q (1 / -1)
-1 = – 4/3 * 1 + b
-1 = – 4/3 + b | + 4/3
– 3/3 +4/3 = b
b = 1/3
–> y= -4/3 x+1/3
Geradengleichung durch einen Punkt und die Steigung bestimmen
Jetzt hast du nur einen Punkt gegeben, der auf der Geraden liegt und dazu die Steigung der Geraden. So kannst du die Geradengleichung auch aufstellen. Hier habe ich für dich die genauen Schritte, die du befolgen solltest:
- Steigung m und den Punkt in die allg. Geradengleichung einsetzen
- Ausrechnen und du erhältst den y-Achsenabschnitt b
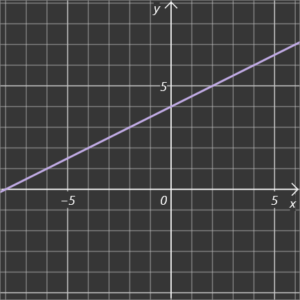
Dann musst du auch hier alle Komponenten (m und b) nehmen und in die allg. Gleichung geben. Und schon kannst du deine Geradengleichung aufstellen.
Natürlich zeige ich dir auch hierfür ein Beispiel.
Beispiel: P (-1 / 4) und m = – 3
1+ 2. Steigung m und den Punkt in die allg. Geradengleichung einsetzen und ausrechnen
4= -3*(-1)+b
4 = 3 + b | -3
1 = b
–> y= -3x+1
Geradengleichung bestimmen durch einen Punkt und dem y-Achsenabschnitt b
Wieder hast du einen Punkt gegeben, der auf der Geraden und dem y-Achsenabschnitt der Geraden liegt. Durch diese Vorgaben kannst du ebenfalls die Geradengleichung aufstellen. Auch hier habe ich eine Vorgehensweise für dich.
- y-Achsenabschnitt b und den Punkt in die allg. Geradengleichung einsetzen
- Ausrechnen und du erhältst die Steigung
Dann musst du auch hier alle Komponenten (m und b) nehmen und in die allg. Gleichung geben. Und schon kannst du deine Geradengleichung aufstellen.
Beispiel: P (2 / 4) und b = 2
1+ 2. y-Achsenabschnitt b und den Punkt in die allg. Geradengleichung einsetzen und ausrechnen.
4=m*2+2 | -2
2 = 2m |: 1
1 = m
–> y=x+2
Geradengleichung bestimmen durch zwei Punkte
Wenn du zwei Punkte, die auf der Geraden liegen gegeben hast, kannst du die Geradengleichung aufstellen. Es gibt 3 Schritte zu Befolgen.
- Steigung berechnen mit der Punkt-Steigungsformel
- Steigung und einen von den zwei Punkten in die allg. Geradengleichung geben
- Ausrechnen und du erhältst den y-Achsenabschnitt b
Dann musst du nur noch alle deine Komponenten (m und b) nehmen und in die allg. Gleichung geben. Und schon kannst du deine Geradengleichung aufstellen.
Natürlich zeige ich dir an einem Beispiel wie das alles funktioniert:
Beispiel: 2 Punkte – P (- 2 / 3) und Q (1 / -1)
1. Setzte die zwei Punkte in die Punkt-Steigungsformel ein
m = (y2 – y1) / (x2 -x1)
m = (- 1 – 3) / (1 – (-2))
m = – 4
2. + 3. m und ein Punkt in die allg. Geradengleichung einsetzten – m = – 4/3 und Q (1 / -1)
-1 = – 4/3 * 1 + b
-1 = – 4/3 + b | + 4/3
– 3/3 +4/3 = b
b = 1/3
–> y= -4/3 x+1/3
Geradengleichung durch einen Punkt und die Steigung bestimmen
Jetzt hast du nur einen Punkt gegeben, der auf der Geraden liegt und dazu die Steigung der Geraden. So kannst du die Geradengleichung auch aufstellen. Hier habe ich für dich die genauen Schritte, die du befolgen solltest:
- Steigung m und den Punkt in die allg. Geradengleichung einsetzen
- Ausrechnen und du erhältst den y-Achsenabschnitt b
Dann musst du auch hier alle Komponenten (m und b) nehmen und in die allg. Gleichung geben. Und schon kannst du deine Geradengleichung aufstellen.
Natürlich zeige ich dir auch hierfür ein Beispiel.
Beispiel: P (-1 / 4) und m = – 3
1+ 2. Steigung m und den Punkt in die allg. Geradengleichung einsetzen und ausrechnen
4= -3*(-1)+b
4 = 3 + b | -3
1 = b
–> y= -3x+1
Geradengleichung bestimmen durch einen Punkt und dem y-Achsenabschnitt b
Wieder hast du einen Punkt gegeben, der auf der Geraden und dem y-Achsenabschnitt der Geraden liegt. Durch diese Vorgaben kannst du ebenfalls die Geradengleichung aufstellen. Auch hier habe ich eine Vorgehensweise für dich.
- y-Achsenabschnitt b und den Punkt in die allg. Geradengleichung einsetzen
- Ausrechnen und du erhältst die Steigung
Dann musst du auch hier alle Komponenten (m und b) nehmen und in die allg. Gleichung geben. Und schon kannst du deine Geradengleichung aufstellen.
Beispiel: P (2 / 4) und b = 2
1+ 2. y-Achsenabschnitt b und den Punkt in die allg. Geradengleichung einsetzen und ausrechnen.
4=m*2+2 | -2
2 = 2m |: 1
1 = m
–> y=x+2
Geradengleichung bestimmen durch zwei Punkte
Wenn du zwei Punkte, die auf der Geraden liegen gegeben hast, kannst du die Geradengleichung aufstellen. Es gibt 3 Schritte zu Befolgen.
- Steigung berechnen mit der Punkt-Steigungsformel
- Steigung und einen von den zwei Punkten in die allg. Geradengleichung geben
- Ausrechnen und du erhältst den y-Achsenabschnitt b
Dann musst du nur noch alle deine Komponenten (m und b) nehmen und in die allg. Gleichung geben. Und schon kannst du deine Geradengleichung aufstellen.
Natürlich zeige ich dir an einem Beispiel wie das alles funktioniert:
Beispiel: 2 Punkte – P (- 2 / 3) und Q (1 / -1)
1. Setzte die zwei Punkte in die Punkt-Steigungsformel ein
m = (y2 – y1) / (x2 -x1)
m = (- 1 – 3) / (1 – (-2))
m = – 4
2. + 3. m und ein Punkt in die allg. Geradengleichung einsetzten – m = – 4/3 und Q (1 / -1)
-1 = – 4/3 * 1 + b
-1 = – 4/3 + b | + 4/3
– 3/3 +4/3 = b
b = 1/3
–> y= -4/3 x+1/3
Geradengleichung durch einen Punkt und die Steigung bestimmen
Jetzt hast du nur einen Punkt gegeben, der auf der Geraden liegt und dazu die Steigung der Geraden. So kannst du die Geradengleichung auch aufstellen. Hier habe ich für dich die genauen Schritte, die du befolgen solltest:
- Steigung m und den Punkt in die allg. Geradengleichung einsetzen
- Ausrechnen und du erhältst den y-Achsenabschnitt b
Dann musst du auch hier alle Komponenten (m und b) nehmen und in die allg. Gleichung geben. Und schon kannst du deine Geradengleichung aufstellen.
Natürlich zeige ich dir auch hierfür ein Beispiel.
Beispiel: P (-1 / 4) und m = – 3
1+ 2. Steigung m und den Punkt in die allg. Geradengleichung einsetzen und ausrechnen
4= -3*(-1)+b
4 = 3 + b | -3
1 = b
–> y= -3x+1
Geradengleichung bestimmen durch einen Punkt und dem y-Achsenabschnitt b
Wieder hast du einen Punkt gegeben, der auf der Geraden und dem y-Achsenabschnitt der Geraden liegt. Durch diese Vorgaben kannst du ebenfalls die Geradengleichung aufstellen. Auch hier habe ich eine Vorgehensweise für dich.
- y-Achsenabschnitt b und den Punkt in die allg. Geradengleichung einsetzen
- Ausrechnen und du erhältst die Steigung
Dann musst du auch hier alle Komponenten (m und b) nehmen und in die allg. Gleichung geben. Und schon kannst du deine Geradengleichung aufstellen.
Beispiel: P (2 / 4) und b = 2
1+ 2. y-Achsenabschnitt b und den Punkt in die allg. Geradengleichung einsetzen und ausrechnen.
4=m*2+2 | -2
2 = 2m |: 1
1 = m
–> y=x+2
Geraden zeichnen
Jetzt wo du Geraden berechnen kannst, sollst du auch Geraden zeichnen können. Alles was du brauchst ist ein Koordinatensystem, eine Geradenfunktion und natürlich ein Geodreieck und einen Bleistift.
- Koordinatensystem richtig beschriften
- y-Achsenabschnitt b einzeichnen
- vom y-Achsenabschnitt die Steigung m einzeichnen und ein Kreuz machen
- vom Kreuz aus noch einmal die Steigung einzeichnen
- alle Punkte mit einer Geraden verbinden
Schon ist die Gerade eingezeichnet.
Auch hier ein Beispiel für dich:
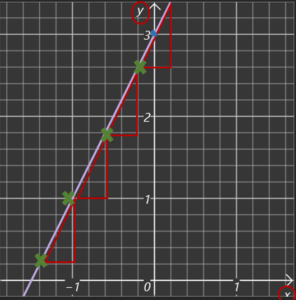
Allgemeine Geraden
Es gibt besondere Geraden, die du unbedingt kennen solltest:
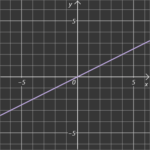
Ursprungsgerade
Diese Gerade geht durch den Nullpunkt 0 (0/0), das heißt, dass b=0 ist
Geradengleichung y = m*x
Senkrechte Gerade
Diese Gerade verläuft parallel zur y-Achse, das heißt, dass m=unendlich ist.
Geradengleichung: x = c
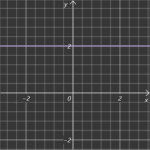
Konstante Gerade
Diese Gerade verläuft parallel zur x-Achse, das heißt, dass m=0 ist.
Geradengleichung: y = c
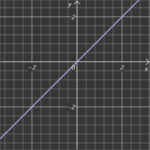
Identität
Diese Gerade geht ebenfalls durch den Nullpunkt.
Geradengleichun:g y = x
Man nennt sie auch Winkelhalbierende des ersten und dritten Quadranten.
Geraden bestimmen – Übungen
Bestimme die Geradengleichung durch die zwei Punkte E (3 / 5) und F ( -1/ 6)
m=(6-5)/(-1-3) = – 1/4
m und Punk t einsetzen
6 = -1/4*(-1)+b |- 1/4
23/4 =b
–> y= -1/4 x+23/4
Bestimme die Geradengleichung durch den Punkt T (1 / 4) und der Steigung m = 3.
4=3*1+b | -3
1=b
–> y=3 x+1
Gerade bestimmen – FAQ
Wie lautet die allg. Geradengleichung?
–> y = m * x + b
Wie lautet die Punkt-Steigungsformel?
m=(y2-y1)/(x2-x1)
Wie berechnet man die Geraden durch 2 Punkten?
- Steigung berechnen mit der Punkt-Steigungsformel
- Steigung und ein von den zwei Punkten in die allg. Geradengleichung geben
- Ausrechnen und du erhältst den y-Achsenabschnitt b
- Geradengleichung angeben
Wie nennt man x-Wert und y-Wert?
x-Werte: Abszisse
y-Werte: Ordinate
