Du hast grad nicht mehr auf dem Schirm, was mit einer Fläche gemeint ist oder wie du den Flächeninhalt berechnen sollst? Wir zeigen es Dir Schritt für Schritt in diesem Artikel.
Flächeninhalt Dreieck? Kein Problem! Hier erfährst du die Formeln und Vorgehensweise für alle wichtigen geometrischen Figuren wie Quadrat, Rechteck, Kreis und co.
Legen wir direkt los!
Fangen wir am besten mal ganz am Anfang an und stellen uns erstmal die Fragen, was eine Fläche überhaupt ist. Mit einer Fläche ist grundsätzlich ein Gebilde gemeint, das sich über eine Länge und eine Breite erstreckt.
Dieser Bereich kann etwa in der Natur oder in der Stadt sein (z.B. ein Grundstück, auf dem ein Haus gebaut wird). Auch ein Blatt Papier oder ein Brett haben eine Fläche.
Die Formeln der Flächenberechnung im Überblick!
Falls du dich schon mit Flächeninhalten auskennst und nur nochmal eine Formel nachschauen wolltest, haben wir hier die wichtigsten einmal für dich zusammengefasst.
\displaystyle A = a⋅a=a^2
\displaystyle A = a⋅b
\displaystyle A = \frac{1}{2}⋅ g⋅h oder \displaystyle A = \frac{g⋅h}{2}
\displaystyle A = \frac{1}{2} ⋅a⋅b
\displaystyle A = \frac{1}{4} ⋅c⋅ \sqrt {4⋅a^2-c^2}
\displaystyle A = \frac{1}{4} ⋅a^2⋅ \sqrt{3}
\displaystyle A = \frac{(a+c)⋅h}{2} oder \displaystyle A = \frac{1}{2} ⋅(a+c)⋅h
\displaystyle A = a⋅h_a
\displaystyle A = a⋅h_a
- Zusammengesetzte Fläche in bekannte Flächen einteilen
- Flächeninhalt dieser mit den bekannten Formeln berechnen
- Berechnete Flächeninhalte addieren
Flächenberechnung – Wie berechnet man den Flächeninhalt geometrischer Figuren?
Nachdem wir Dir kurz erklärt haben, was der Flächeninhalt ist, möchten wir Dir in den nachfolgenden Abschnitten 7 bekannte geometrische Figuren, ihre Eigenschaften sowie die dazugehörige Formel zur Berechnung des Flächeninhalts vorstellen.
Denn jede einzelne Figur hat ihre eigene Formel, mit der du den Flächeninhalt einfach berechnen kannst.
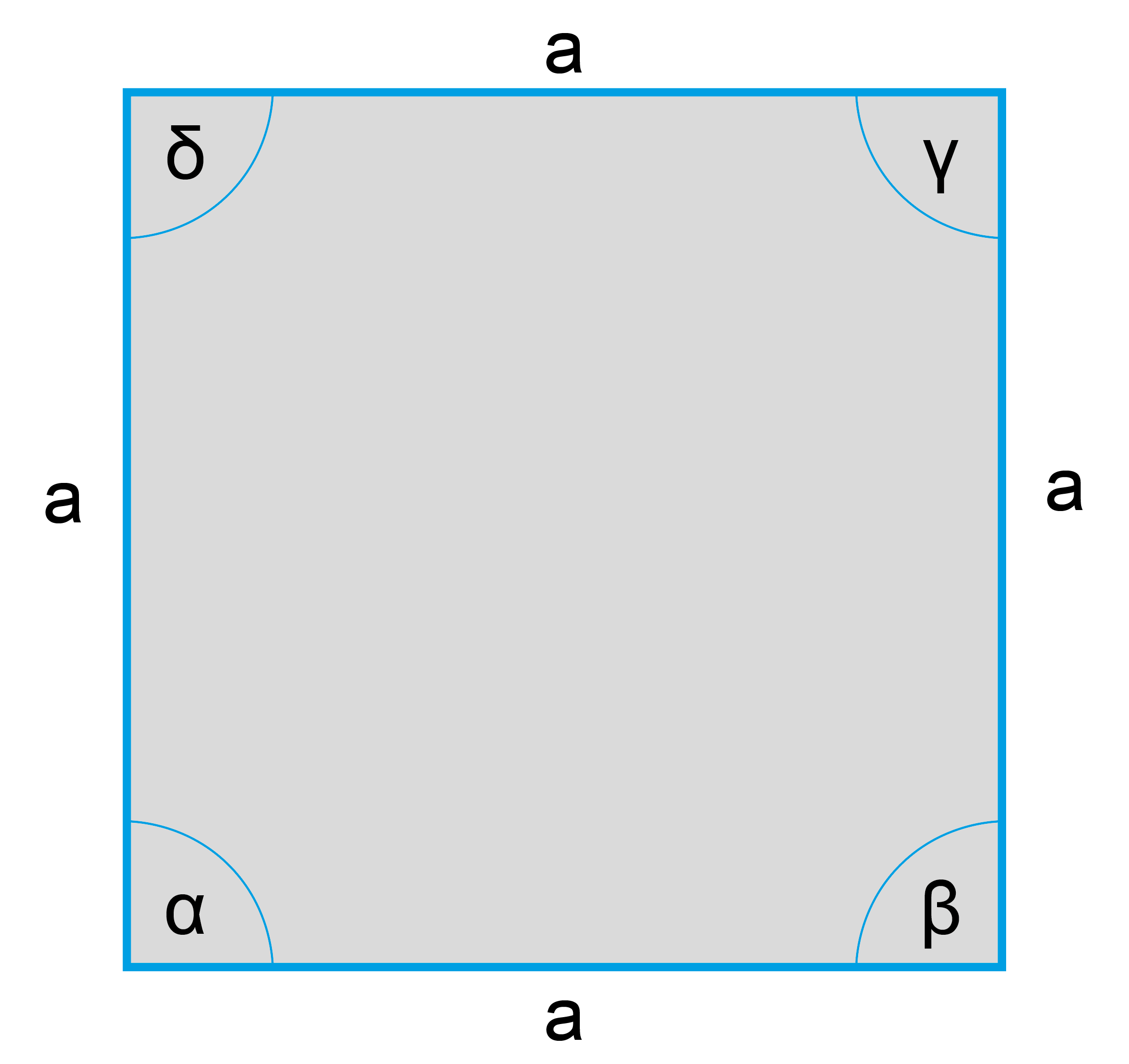
Flächeninhalt Quadrat
Eigenschaften Quadrat | |
Seiten: | Alle vier Seiten “a” sind gleich lang. |
Winkel: | α = β = γ = δ = 90° |
Winkelsumme: | (α + β + γ + δ) beträgt 360° |
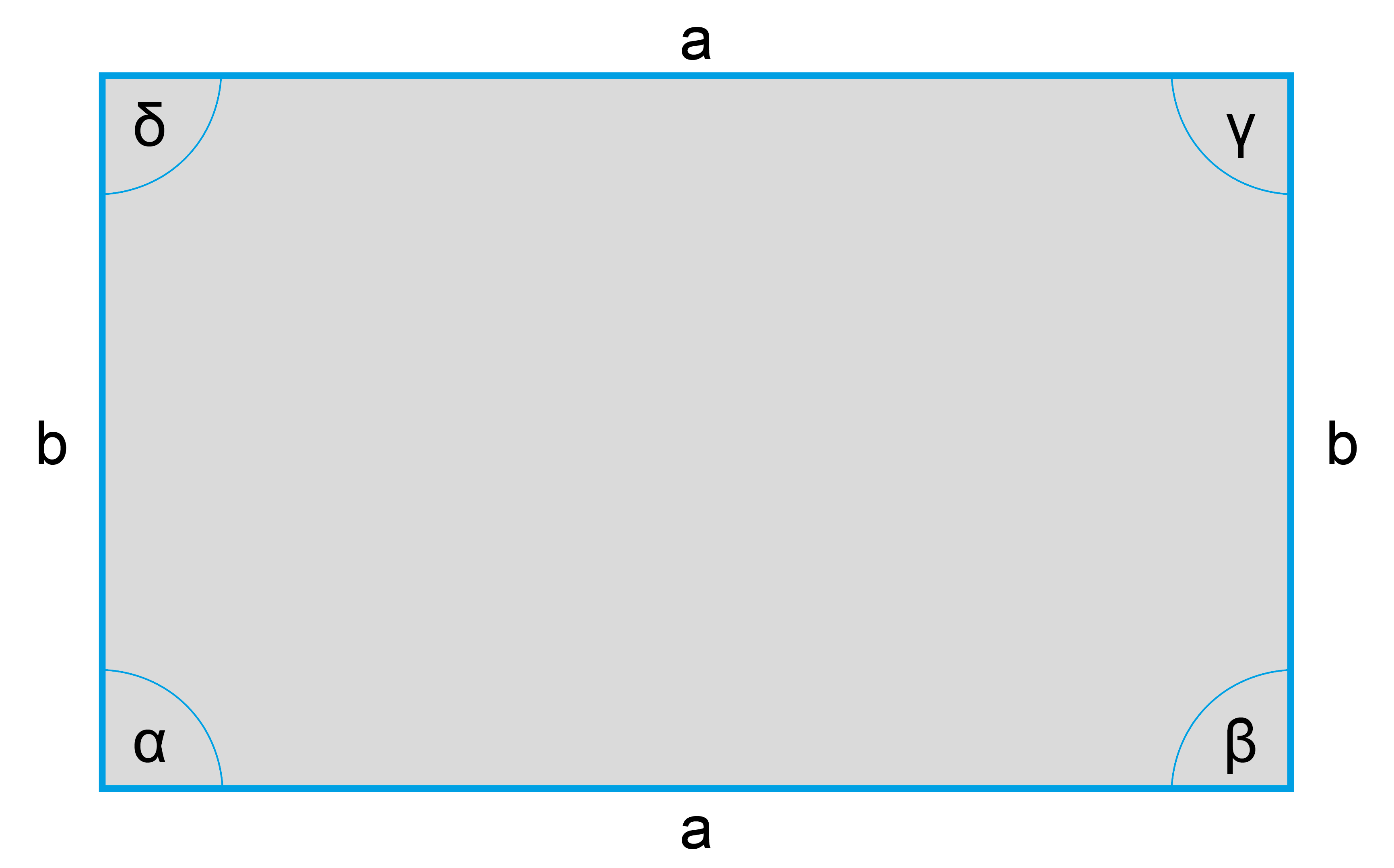
Flächeninhalt Rechteck
Eigenschaften Rechteck | |
Seiten: | Die jeweils Gegenüberliegenden Seiten sind parallel und gleich lang. |
Winkel: | α = β = γ = δ = 90° |
Winkelsumme: | (α + β + γ + δ) beträgt 360° |
Die Herleitung der Formel haben wir bereits einfach und verständlich erklärt.
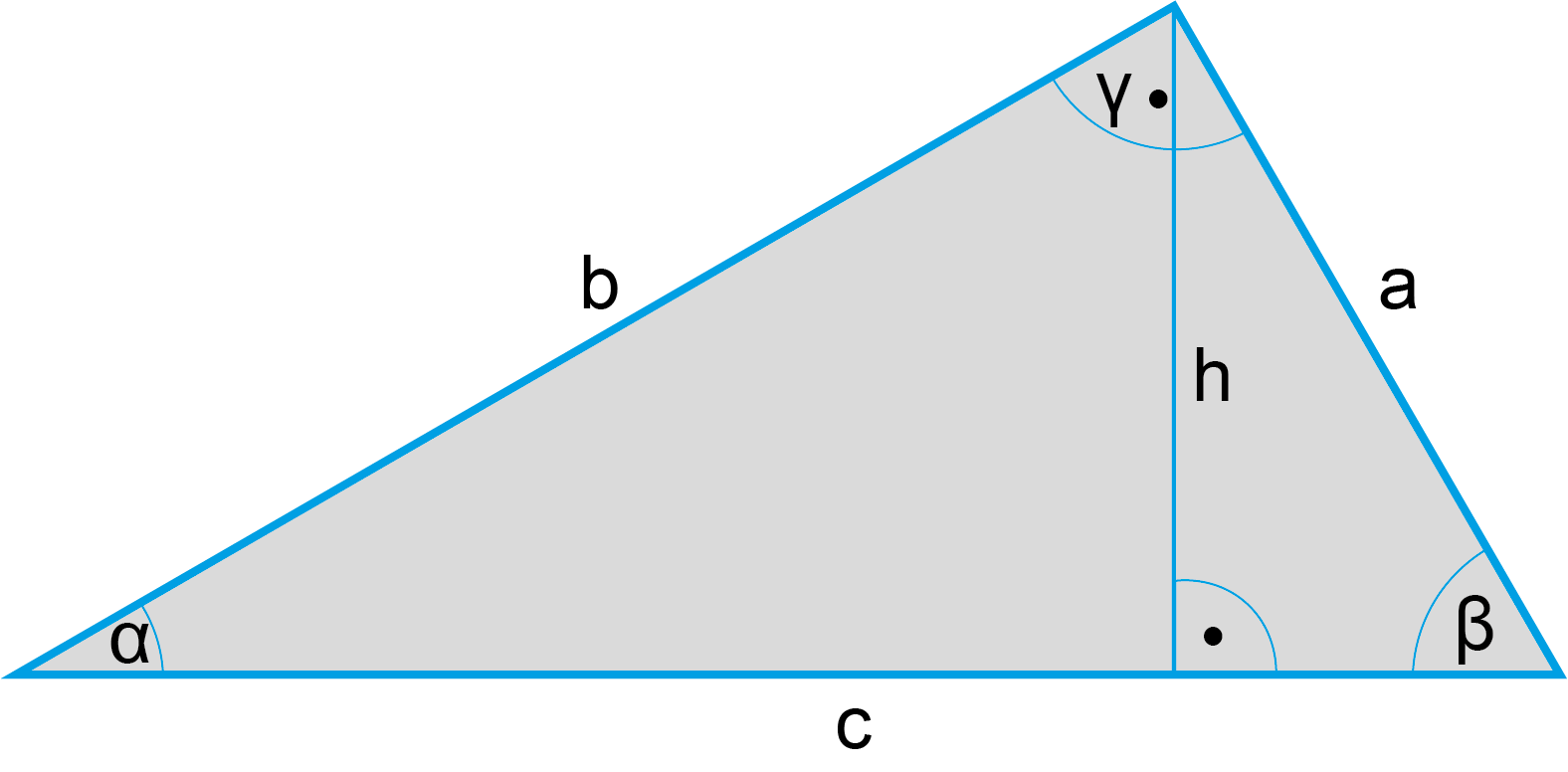
Flächeninhalt Dreieck
Allgemeines Dreieck
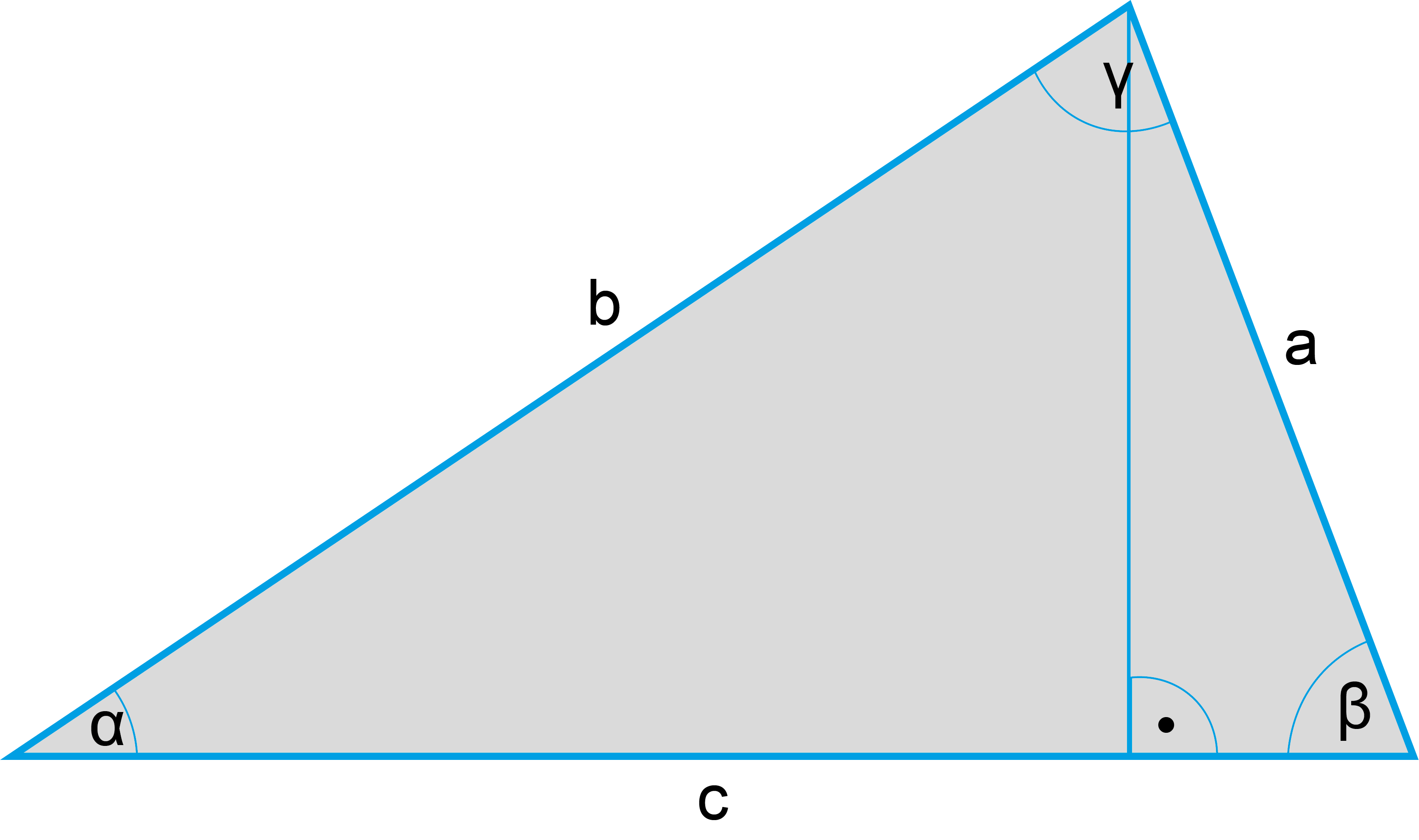
Rechtwinkliges Dreieck
Rechtwinkliges Dreieck | |
Seiten: | Hat drei Seiten (a, b, c). |
Winkel: | α + β = 90° γ = 90° |
Winkelsumme: | (α + β + γ) beträgt 180° |
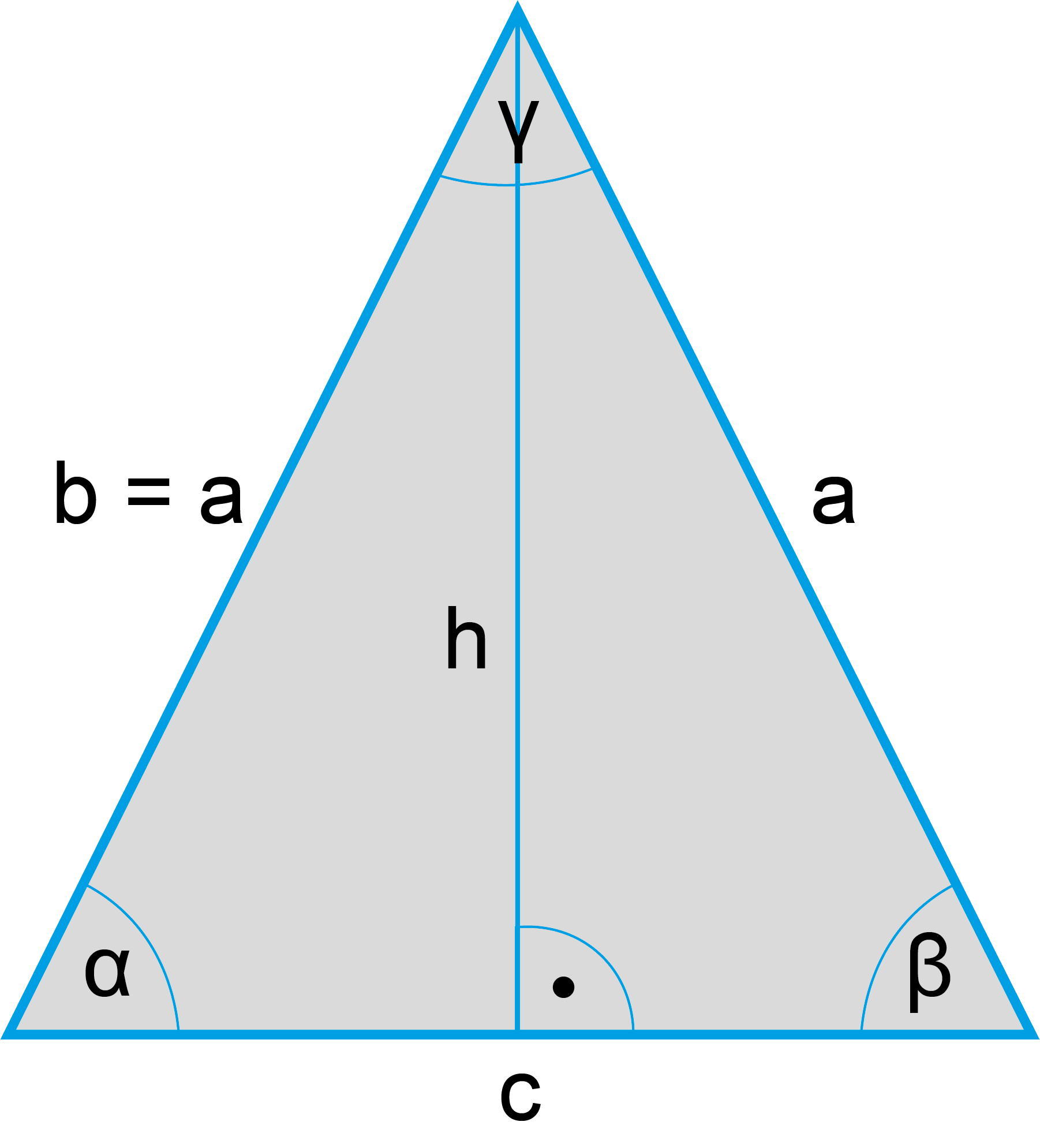
Gleichschenkliges Dreieck
Gleichschenkliges Dreieck | |
Seiten: | Hat drei Seiten (a, b, c). |
Winkelsumme: | (α + β + γ) beträgt 180° |
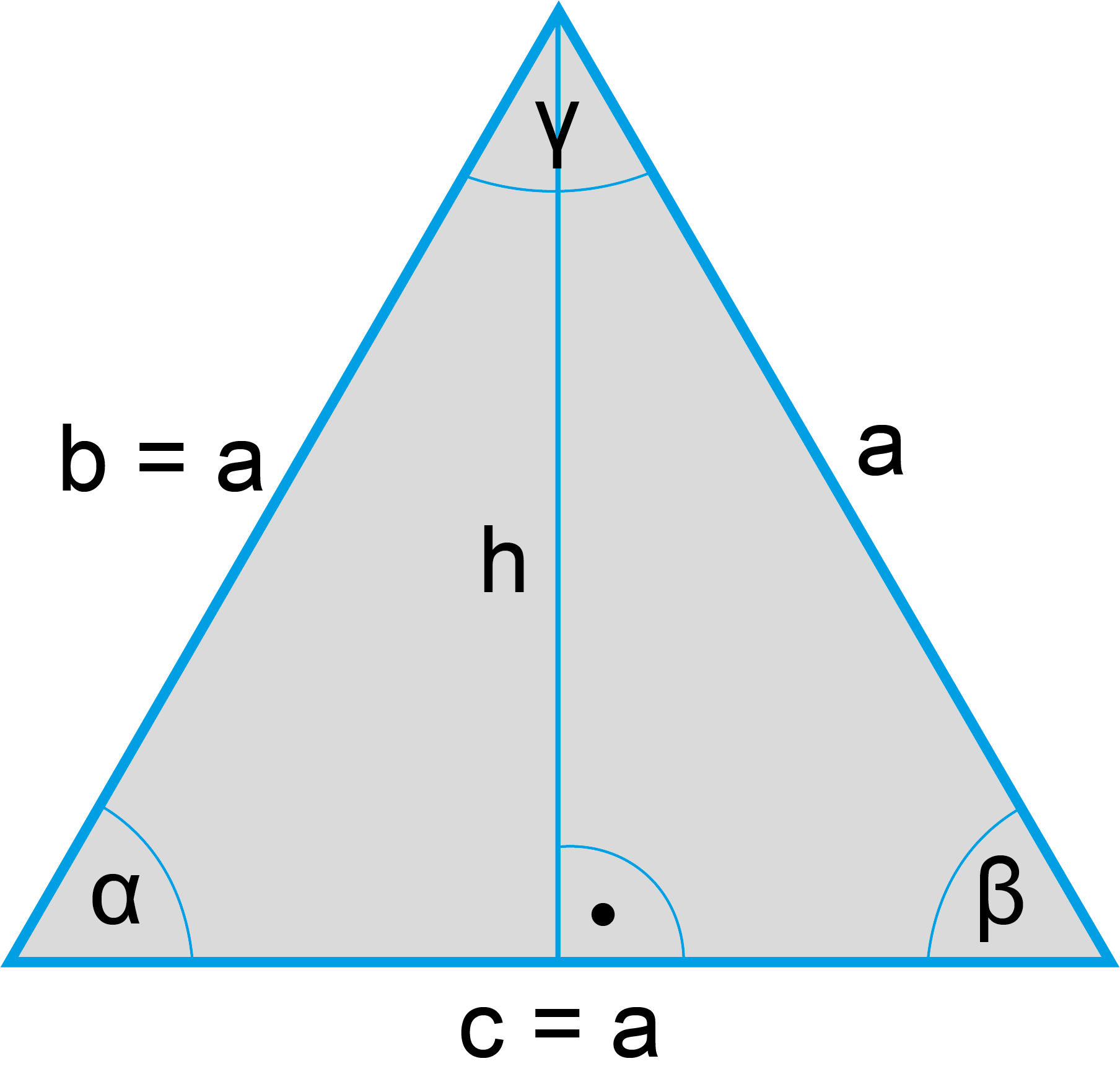
Gleichseitiges Dreieck
Gleichseitiges Dreieck | |
Seiten: | Hat drei Seiten (a, b, c). |
Winkel: | α = β = γ = 60° |
Winkelsumme: | (α + β + γ) beträgt 180° |
Weitere Formeln rund ums Dreieck sowie Übungsaufgaben mit Lösungen findest du in unserem Artikel Dreieck berechnen.
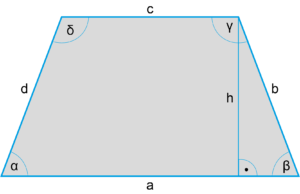
Flächeninhalt Trapez
Eigenschaften Trapez | |
Seiten: | Ein Trapez hat zwei parallele Seiten (a ‖ c). |
Höhe h: | Die Höhe entspricht dem Abstand der beiden parallelen Seiten (a ‖ c). |
Winkel: | α + δ = 180° |
Winkelsumme: | (α + β + γ + δ) beträgt 360° |
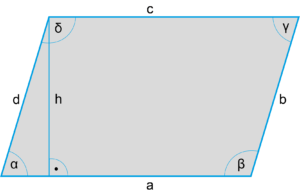
Flächeninhalt Parallelogramm
Eigenschaften Parallelogramm | |
Seiten: | Die Gegenüberliegenden Seiten sind parallel und gleich lang. |
Höhe h: | Der Abstand der parallelen Seiten, entspricht der Höhe des Parallelogramms. |
Winkel: | Gegenüberliegende Winkel sind gleich groß. |
Winkelsumme: | (α + β + γ + δ) beträgt 360° |
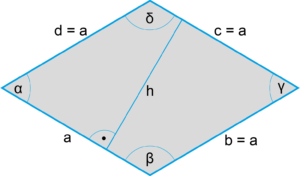
Flächeninhalt Raute
Eigenschaften Raute | |
Seiten: | Mit vier gleich langen Seiten, ist die Raute ein Parallelogramm. |
Höhe h: | Die Höhe entspricht dem Abstand der parallelen Seiten. |
Winkel: | Die gegenüberliegenden Winkel sind gleich groß (α = γ) und (β = δ). |
Winkelsumme: | (α + β + γ + δ) beträgt 360° |
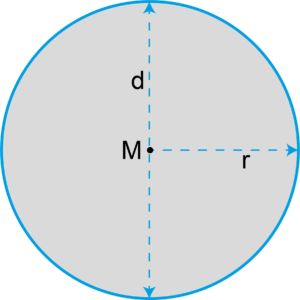
Flächeninhalt Kreis
Eigenschaften Kreis | |
Bezeichnungen: | M = Mittelpunkt |
Radius r: | Der Radius ist halb so lang wie der Durchmesser. |
Durchmesser d: | Der Durchmesser ist doppelt so lang wie der Radius. |
Zusammengesetzte Flächen – Wie soll ich das denn berechnen?
Du weißt jetzt wie man den Flächeninhalt jeder geometrischen Figur berechnet, die so im Matheunterricht vorkommt.
Aber was ist denn, wenn plötzlich so eine Form in der Mathearbeit ist?
Ruhe bewahren und nicht verzweifeln! Eigentlich siehst du hier nichts anderes als, die Formen, die du schon kennengelernt hast.
Um den Flächeninhalt von so einer zusammengesetzten Form zu berechnen, musst du diese nur in kleinere, dir bekannte Formen aufteilen.
Im Anschluss berechnest du dann die einzelnen Flächeninhalte wie gerade gelernt. Um den gesamten Flächeninhalte der zusammengesetzten Form zu berechnen musst du deine einzelnen Ergebnisse dann nur noch addieren.
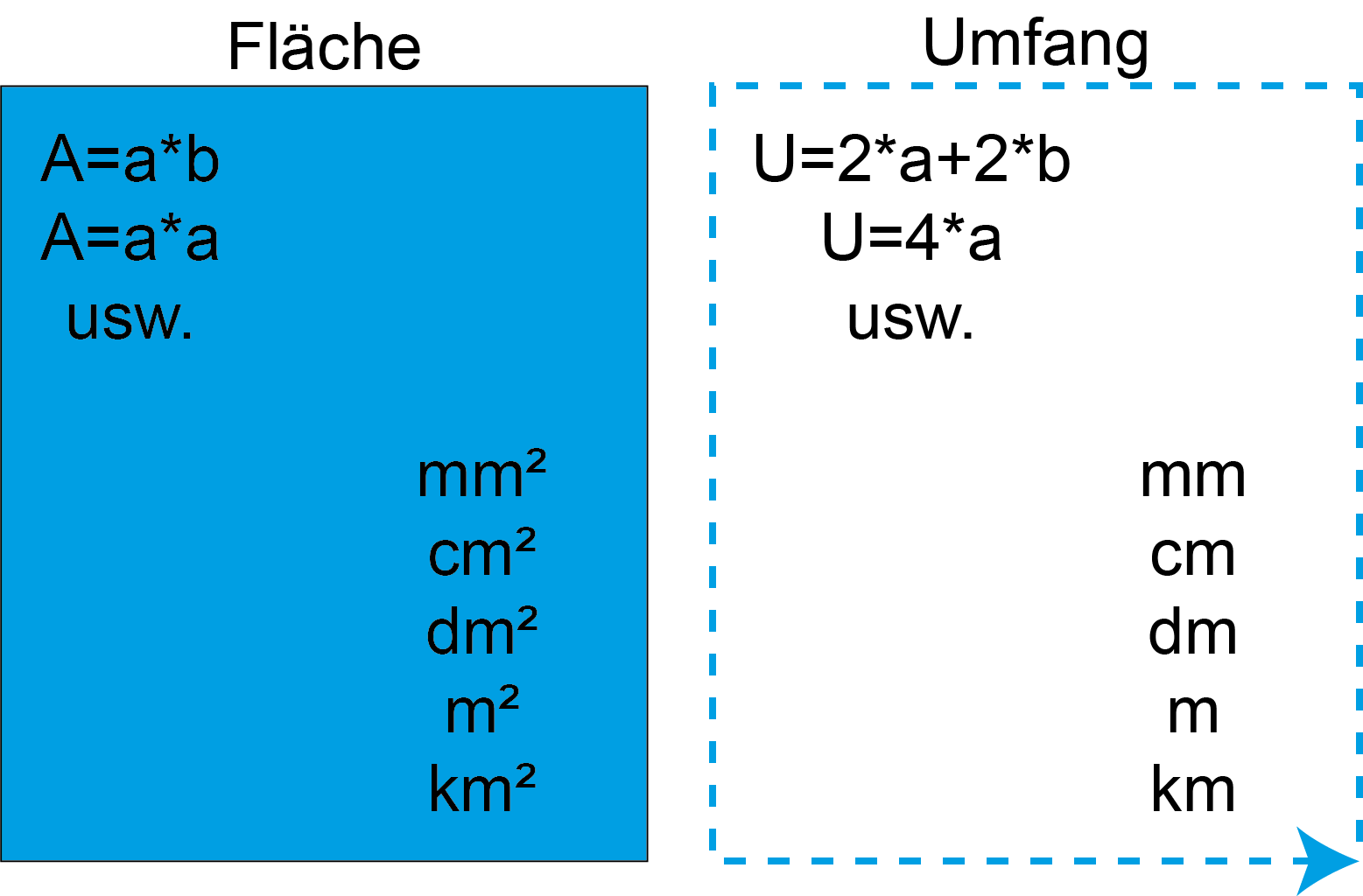
Flächeninhalt und Umfang – ein großer Unterschied
Flächeninhalt | Umfang |
Die Fläche berechnet sich meist aus Länge mal Breite. | Für den Umfang zählst Du alle Seiten, der Figur, zusammen. |
Das Maß für die bestimmte Fläche ist immer Quadratzentimeter, Quadratmeter, usw. | Das Maß für den Umfang ist immer Zentimeter, Meter, usw. |
Stell dir als Beispiel einen Garten vor: Mit dem Flächeninhalt ist gemeint, wie viel Rasenfläche dein Garten hat. Der Umfang sagt dir dann wie viel Zaun du bräuchtest, um deinen Garten komplett umzäunen zu können.
Flächeninhalt berechnen – FAQ
Was ist die Formel vom Flächeninhalt?
Die Formel vom Flächeninhalt ist bei jeder (geometrischen) Figur unterschiedlich. Hier sind die Formeln für die bekanntesten geometrischen Figuren:
- Rechteck: A=a*b
- Raute: A=a∗ha
- Parallelogramm: A=a∗ha
- Trapez: 0,5∗(a+c)∗h
- Dreieck: 0,5∗g∗h
- Quadrat: a²
Was ist Flächeninhalt und Umfang?
Der Flächeninhalt, ist ein Maß für eine Größe einer Fläche von einer bestimmten Figur. Und der Umfang (einer Figur) ist die Summe aller Seitenlängen, damit ist die Länge der Begrenzungslinie gemeint.
Wie berechnet man Flächeninhalt und Umfang?
Die Berechnungen des Flächeninhaltes und des Umfanges variieren bei jeder (geometrischen) Figur.
Beispiel: Rechteck
- Flächeninhalt Formel: A = a*b
- Umfang Formel: U = 2*a + 2*B
Wenn du noch andere Mathethemen suchst, kannst du dich gern auf unserer Seite umschauen. Hier findest alles von Gewichte umrechnen bis hin zu den Linearen Gleichungen.
Hast du es vielleicht allgemein nicht so mit den Zahlen? Dann wäre Mathe Nachhilfe sehr wahrscheinlich genau das Richtige für dich.
Hier kannst du ganz einfach mit der Mathe Nachhilfe oder der Online Mathe Nachhilfe anfangen.
Wenn du dich vorher noch mehr über das Thema informieren möchtest, findest du hier alle Infos zu unseren Nachhilfe-Leistungen.


Super übersichtlich, finde keine Möglichkeit zum Drucken
Rechtsklick => Drucken oder alternativ Strg + P drücken
Strg und P gleichzeitig
ich bin 77 jahre alt und manchmal muss ich mein wissen auffrischen bzw. absichern, für diese seiten ein dankeschön.
Sehr gut, durch diese Seite konnte ich für meine bevorstehende Prüfung lernen.