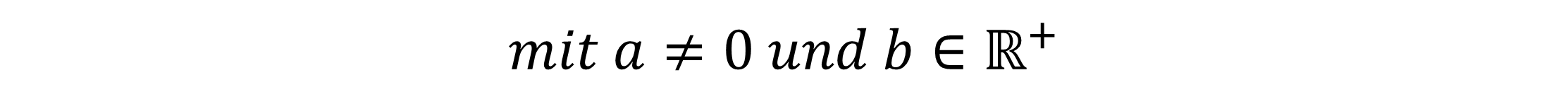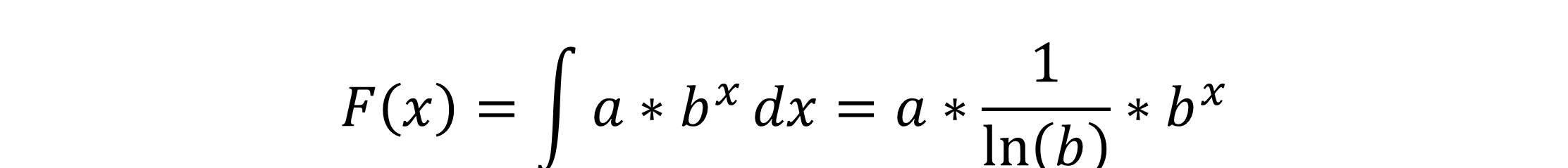Exponentialfunktion leichtverständlich erklärt mit Beispielen

In diesem Artikel erklären wir dir, was die Exponentialfunktion ist, wie du sie aufstellst und wie du sie ableiten, sowie integrieren kannst. Das ganze wird dir anschaulich mit Beispielen präsentiert.

Und los geht’s!

Exponentialfunktion Definition

Mit der Exponentialfunktion ist es dir möglich, exponentielles Wachstum zu beschreiben. Dabei steigt der Graph nicht wie bei linearem Wachstum mit der immer gleichen Steigung an, sondern wird immer steiler.

Du darfst die Exponentialfunktion nicht mit der Potenzfunktion (z.B. f(x)=x²) verwechseln. Die Exponentialfunktion ist nach der Form f(x)=a*b^x aufgebaut, während die Potenzfunktion die Form f(x)=a*xⁿ hat.

Beispiele für ein exponentielles Wachstum sind Epidemien oder die Ausbreitung des Corona-Virus in 2020. Bei dieser hat sich die Anzahl der Infizierten alle paar Tage verdoppelt. Auch die Population von Mikroorganismen entwickelt sich in der Anfangszeit exponentiell.

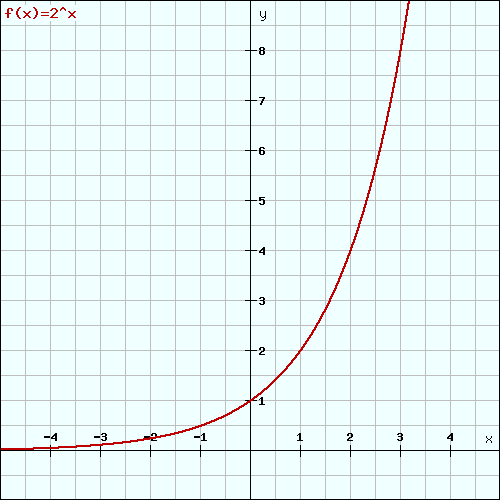
Die Exponentialfunktion wird immer durch einen Graphen mit ähnlicher Form zu dem folgenden Bild dargestellt. An diesem kannst du erkennen, dass sich eine Exponentialfunktion immer x=0 annähert, jedoch nie die x-Achse schneiden wird:

Exponentialfunktion Formel

Die Funktion für die allgemeine Exponentialfunktion lautet:

Bei dieser Formel steht die Variable x immer im Exponenten. Das “a” steht für den Anfangswert und kann jeden beliebigen Wert außer Null haben. Die Basis “b” gibt an, wie steil unser Graph verläuft.

Das Bild von dem Graph aus dem vorherigen Abschnitt stellt die Funktion f(x)=2^x dar. Hierfür sind der Anfangswert a=1 und die Basis b=2. Somit verdoppelt sich der Y-Wert, wenn der Wert auf der X-Achse um eine Einheit steigt (x=1, y=2; x=2, y=4; x=3, y=8).

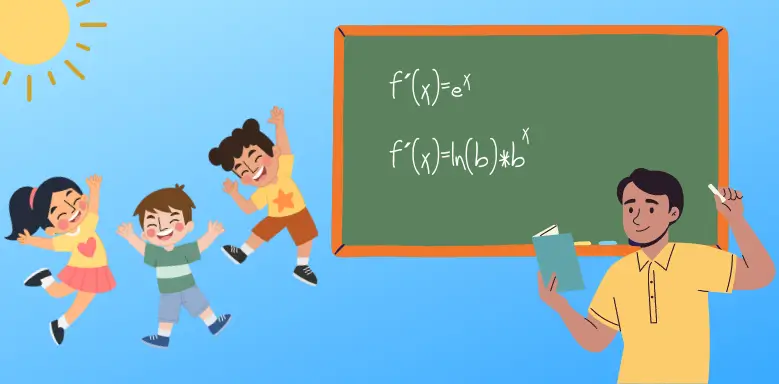
Exponentialfunktion ableiten

Wir zeigen dir jetzt, wie du die natürliche Exponentialfunktion also mit e als Basis und auch Exponentialfunktionen mit anderer Basis ableiten kannst.

Exponentialfunktion e – Sonderfall natürliche Exponentialfunktion

Die Basis e hat  ungefähr den Wert 2,7182. Deshalb ist die besondere Eigenschaft der natürlichen Exponentialfunktion, dass die Ableitung der Funktion die Funktion selbst ist:

Funktionen mit anderer Basis ableiten

Wenn du statt e eine andere Basis hast, kannst du diese Exponentialfunktion natürlich auch ableiten. Hierbei kriegst du neben der gleichbleibenden Basis “b” hoch x noch einen Vorfaktor ln(b) durch die Ableitung:

Zur anschaulichen Darstellung für dich ein Beispiel mit dem Wert 3 als Basis “b”.

Das Integral bilden

Wenn du das Integral für die Exponentialfunktion bilden möchtest, musst die Ableitung sozusagen rückgängig machen. Dafür teilst du 1 durch den natürlichen Logarithmus von der Basis “b”.

Exponentialfunktion Eigenschaften

Du kannst durch das Einsetzen von unterschiedlichen Werten für “a” und “b” den Verlauf des Funktionsgraphen beeinflussen. Die verschiedenen Möglichkeiten zeigen wir dir jetzt:

Steigung beeinflussen

Wenn du für den Anfangswert “a” unterschiedliche Werte einsetzt, kannst du die Schnelligkeit der Steigung beeinflussen. Um dir das ganze anschaulich darzustellen, nehmen wir 3 verschiedene Funktionen mit unterschiedlichem Wert für “a” und der gleichen Basis b=2:

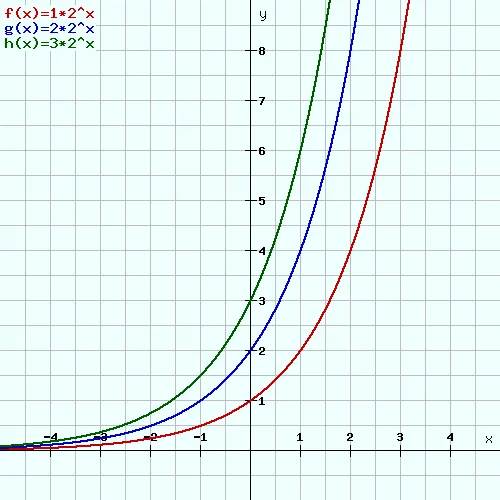
Wie du sehen kannst, haben wir für “a” die Werte 1, 2 und 3 eingesetzt. Je größer dieser Wert ist, desto schneller steigt unsere Exponentialfunktion streng monoton an.

Der Wert für “a” gibt außerdem den Punkt an, in dem der Graph die Y-Achse schneidet. Hier also die Punkte (0|1), (0|2) und (0|3).

Exponentieller Zerfall  

Wenn du für die Basis “b” einen Wert im Intervall zwischen 0 und 1 wählst (z.B. 0,5) , dann fällt die Exponentialfunktion. Auch hier zeigen wir dir das ganze an einem Graph.

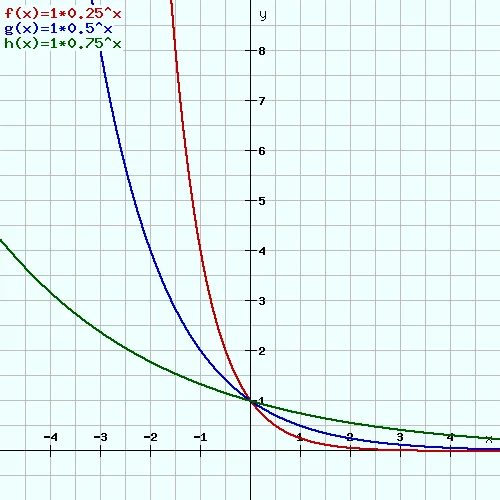
Wir haben für “b” die Werte 0,25, 0,5 und 0,75 eingesetzt und “a” hat gleichbleibend den Wert 1. Je kleiner der Wert für “b” ist, desto schneller fällt der Funktionsgraph. Diese streng monoton fallenden Exponentialfunktionen lassen sich auch als exponentieller Zerfall bezeichnen.

Die Funktion spiegeln

Wenn du für den Anfangswert “a” ein negatives Vorzeichen einsetzt, dann führt das zu einer Spiegelung des Graphen an der X-Achse.

Damit du das ganze besser nachvollziehen kannst, hier zwei Bilder von Graphen einmal für b=2 (links) und das andere für b=0,5 (rechts). Es ändert sich bei beiden nur der Wert von “a” von 1 zu -1:

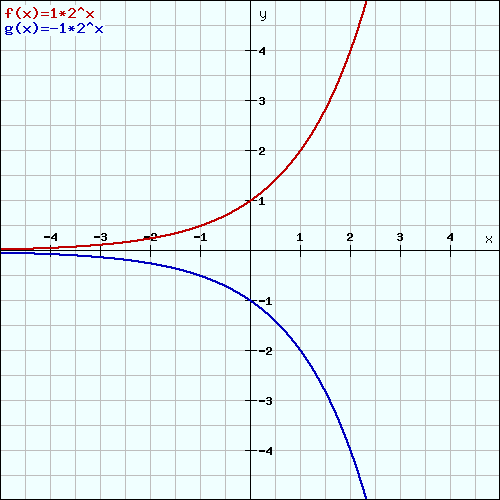
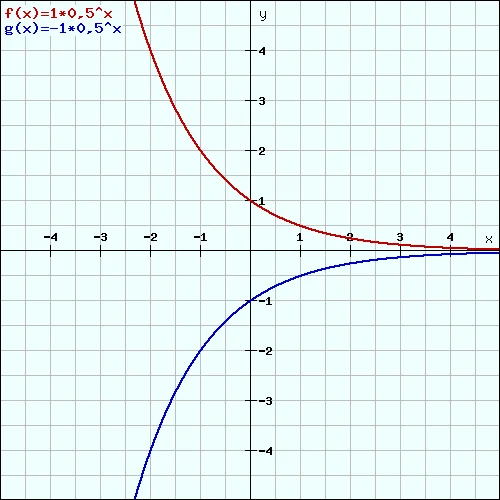
Verschiebung entlang der Y-Achse

Du kannst die Exponentialfunktion mithilfe des Parameters “d” entlang der Y-Achse nach oben und unten verschieben. Die Formel nimmt dann die folgende Form an:

Damit das alles für dich anschaulich ist, zeigen wir dir das Ganze an Hand von ein paar Graphen. Unsere Exponentialfunktion setzt sich immer aus dem allgemeinen Teil f(x)=2^x und dem Wert für “d” (0, 2, -2) zusammen, der sich variieren lässt:

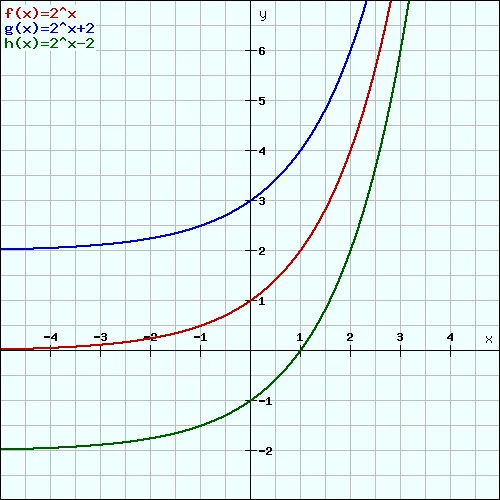
Exponentialfunktion zeichnen

Wenn du eine Exponentialfunktion hast und schnell gucken möchtest wie der Verlauf des Graphen ist, dann nutz doch das Online-Tool, das wir zum Erstellen der Graphen genutzt haben.