Du kennst die Eulersche Zahl aus der Schule oder der Uni, möchtest aber noch mehr dazu erfahren?
Wir zeigen dir hier was die Eulersche Zahl ist und was sie so besonders für die Mathematik macht. Das alles wird dir nachvollziehbar mit anschaulichen Formeln und Herleitungen erklärt.
Lass uns starten!
Die eulersche Zahl e ist eine der wichtigsten Zahlen der Mathematik und Wissenschaft und hat den Wert:
Du kennst sie bestimmt schon aus ihren häufigsten Anwendungsbereichen, dem Sonderfall der Exponentialfunktion, der e-Funktion ex und dem natürlichen Logarithmus, dem Logarithmus zur Basis e.

Eigenschaften
Die Eulersche Zahl hat einige Eigenschaften, die diese besonders machen.
Eulersche Zahl Nachkommastellen
Und damit sind wir schon beim ersten Punkt, der die e-Zahl so besonders macht. Sie hat nämlich unendlich viele Nachkommastellen, die sich NICHT mit einem regelmäßigen Muster wiederholen. Deshalb kannst du sie als
nicht abbrechend und
nicht periodisch bezeichnen.
Eulersche Zahl irrational
Aufgrund dieser Eigenschaften aus dem vorherigen Abschnitt kannst du die eulersche Zahl zu den irrationalen Zahlen zählen.
Du musst dir jedoch merken, dass diese im Gegensatz zu anderen irrationalen Zahlen sich nicht geometrisch konstruieren lässt. Deshalb gehört sie zu den transzendenten Zahlen.

Ableitung und Aufleitung
Eulersche Zahl ableiten
Wenn du die e-Funktion, also die natürliche Exponentialfunktion ableiten willst, gibt es eine Besonderheit. Die Ableitung der Funktion ex ist nämlich die Funktion selbst:
Integral
Wenn du die natürliche Exponentialfunktion integrieren möchtest, dann musst du zu der Stammfunktion wie immer noch die Konstante C dazu addieren:

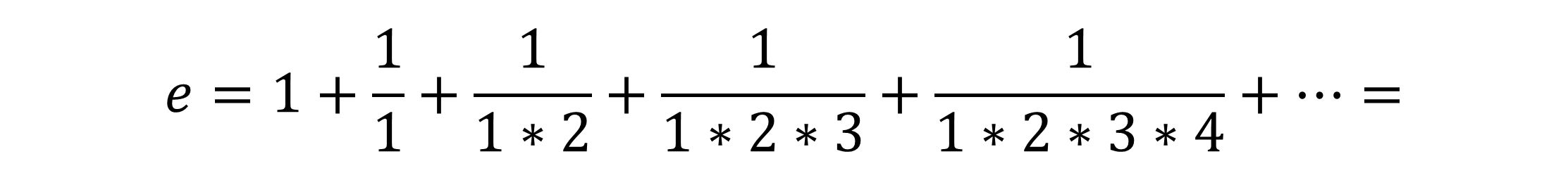
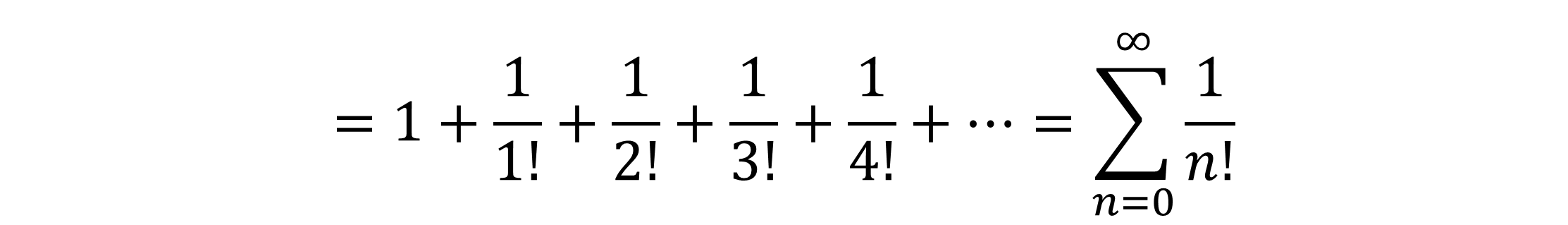
Hi,
es heißt integrieren. In der Schule bekommt man auf den Deckel, wenn man “Aufl..” sagt.