Wir zeigen dir Schritt für Schritt, wie du ganz simpel einen Dreisatz berechnen kannst und erklären dir die Begriffe proportionaler und antiproportionaler Dreisatz. Dein Wissen kannst du am Ende des Artikels mit unseren Übungsaufgaben direkt anwenden und austesten 🙂
Los geht’s!
Dreisatz einfach erklärt – Wann wird er gebraucht?
Der Dreisatz ist ein Lösungsverfahren in der Mathematik, mit dem du aus dem Verhältnis zwischen 2 bekannten Größen eine unbekannte Größe berechnen kannst.
Die Bezeichnung “Dreisatz” ergibt sich aus den 3 Schritten des Rechenwegs.
Mit dem Dreisatz lassen sich Proportionalaufgaben berechnen. Auch im Alltag ist die Anwendung des Dreisatz ein hilfreiches Mittel. Du kannst mit ihm unter anderem
- Preise im Supermarkt ausrechnen
- Mengenangaben beim Kochen oder Backen ermitteln
- Prozentsätze berechnen
Um den Dreisatz zu berechnen, ist es ratsam, die Multiplikation und Division zu beherrschen. Wir zeigen dir in den folgenden Abschnitten Schritt für Schritt, wie die Berechnung des Dreisatzes abläuft.
Proportionaler Dreisatz
Der klassische Dreisatz wird auch proportionaler Dreisatz genannt. Zwei Mengen bzw. Größen stehen im proportionalen Verhältnis zueinander. Die Werte steigen oder sinken also im gleichen Verhältnis: je mehr von X, desto mehr von Y.
Beispiel:
Stell dir vor, du möchtest drei Packungen Kekse kaufen. Eine Packung Kekse kostet 0,75 €. Dann kosten zwei Packungen Kekse dopppelt so viel (1,50 €) und drei Kekspackungen dreimal so viel (2,25 €). Das ist ein proportionales Verhältnis.
Proportionalen Dreisatz berechnen mit der Dreisatz Formel
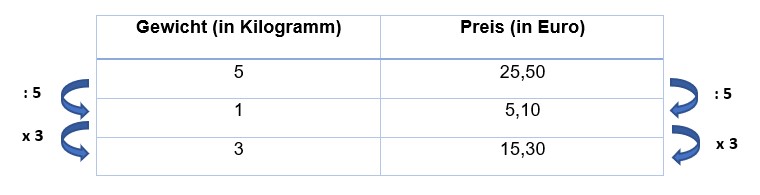
Zunächst wollen wir den Rechenweg anhand einer Aufgabe und einer Tabelle veranschaulichen.
Die Aufgabenstellung in einer Mathearbeit könnte lauten:
“Ihr steht im Supermarkt an der Käsetheke und wollt 3 kg Gouda kaufen. 5 Kilogramm Gouda kosten 25,50 Euro. Wieviel kosten 3 Kilogramm?”
Der Lösungweg ist eigentlich ganz einfach:
- Schritt 1: Datenerfassung
→ 5 kg Käse kosten 25,50 € - Schritt 2: Preis für 1 kg berechnen
→ 1 kg Käse kosten 25,50 : 5 = 5,10€ - Schritt 3: Preis für 3 kg berechnen
→ 3 kg Käse kosten 5,10 • 3 = 15,30
Hat man einmal den Rechenweg des proportionalen Dreisatzes verinnerlicht, kann man auch ohne Tabelle arbeiten und stattdessen direkt die Formel anwenden:
Antiproportionaler Dreisatz bzw. umgekehrter Dreisatz
Der antiproportionale Dreisatz wird auch umgekehrter Dreisatz genannt. Beim antiproportionalen Dreisatz stehen zwei Größen in einem antiproportionalen Zusammenhang. Hier gilt also: Je mehr von Größe X, desto weniger von Größe Y.
Beispiel:
Stell dir vor, beim Supermarkt kommt eine neue Warenlieferung an. Drei Arbeitskräfte sollen die Waren in die Regale einsortieren. Sie brauchen dafür 10 Stunden. Werden allerdings drei zusätzliche Mitarbeiter angefordert, brauchen alle sechs gemeinsam nur halb so viel Zeit, also 5 Stunden.
Antiproportionalen Dreisatz berechnen – Formel
Auch in diesem Fall kann man den Rechenweg sehr gut mit einer Tabelle veranschaulichen. Doch schauen wir uns zunächst eine Beispielaufgabe an.
“Drei Mitarbeiter des Finanzamts brauchen 32 Stunden, um die Abrechnung eines wichtigen Kunden fertigzustellen. Wie viele Stunden werden insgesamt benötigt, wenn acht Mitarbeiter an der Abrechnung arbeiten?”
Auch hier besteht der Rechenweg wieder aus 3 Schritten:
- Schritt 1: Datenerfassung
→ 3 Mitarbeiter benötigen 32 Arbeitsstunden - Schritt 2: Stunden für einen Mitarbeiter berechnen
→ 1 Mitarbeiter alleine benötigt 32 Stunden • 3 = 96 Arbeitsstunden - Schritt 3: Stunden für 8 Mitarbeiter berechnen
→ 8 Mitarbeiter benötigen 96 Stunden : 8 = 12 Arbeitsstunden
Eigentlich ganz einfach oder? Der wichtigste Schritt ist zu erkennen, dass es sich um eine antiproportionale Zuordnung handelt, denn je mehr Mitarbeiter am selben Projekt arbeiten, desto weniger Zeit wird insgesamt benötigt.
Die Tabelle dient der Veranschaulichung. Natürlich könnt ihr die Lösung auch einfach mit der Formel ermitteln:
Prozentrechnung Dreisatz
Einen Prozentsatz mit dem Dreisatz zu berechnen, ist nicht schwer.
Stelle dir das folgende Beispiel vor:
Du arbeitest in einer Pizzeria. Am Tag kannst du mit dem vorbereiteten Teig 200 Pizzen herstellen. Das wäre eine 100% -ige Auslastung.
Nun willst du wissen, wie viel Prozent die Herstellung von nur 120 Pizzen am Tag bedeuten würden. Du kannst nun ganz einfach den Dreisatz anwenden:
Dreisatz rechnen lernen – Good to know
Folgendes solltest du bei der Dreisatzrechnung beachten:
- Aufgabenstellung anschauen: Oft gibt die Aufgabenstellung bereits wichtige Informationen darüber, wie du den Dreisatz verwenden sollst. Überlege dir genau, welche Art von Dreisatz (proportional oder antiproportional) gerechnet werden muss.
- Datenerfassung: Schreibe dir auf, welche Werte dir bereits vorliegen und welcher Zielwert errechnet werden soll.
- Tabelle als Hilfsmittel: Tabellen sind ein tolles Hilfsmittel, um die Rechenwege besser nachvollziehen zu können. Es lohnt sich also, für deine Werte eine Tabelle anzulegen und die einzelnen Schritte festzuhalten.
Dreisatz Aufgaben mit Lösungen
Abschließend haben wir für dich drei Aufgaben zur Dreisatzberechnung zusammengetragen, bei denen du das Gelernte direkt anwenden kannst. Klick einfach auf das Plus-Zeichen (+), um dein Ergebnis zu kontrollieren. Los geht’s!
Ein Bauernhof hat mehrere Kühe. Diese können alle 2 Tage insgesamt 400 Liter Milch geben. Die Molkereiartikel werden an mehrere Supermärkte weiterverkauft. Aufgrund einer hohen Nachfrage an Molkereiartikeln muss der Bauer 1500 Liter innerhalb von 7 Tagen produzieren. Ist es möglich dass der Bauernhof den Nachfrageanstieg stemmen kann?
Milchertrag pro Tag: 400 Liter ÷ 2=200 Liter
Milchertrag für 7 Tage: 200 Liter · 7 = 1400 Liter
1500 Liter – 1400 Liter = 100 Liter
Antwort: Nein, der Bauer bekommt in 7 Tagen nur 1400 Liter Milch von seinen Kühen. Das sind 100 Liter zu wenig.
3 Packungen Mehl wiegen 1,5kg. Wie schwer sind 5 Packungen Mehl?
1,5kg = 1500g
Gewicht pro Packung: 1500 ÷ 3 Packungen = 500g
Gewicht für 5 Packungen: 500g · 5 Packungen = 2500g
Antwort: 5 Packungen Mehl wiegen 2,5 Kilogramm.
In NRW soll ein Waldstück gerodet werden. Es werden 3 Bagger eingesetzt. Diese benötigen für die Arbeit 21 Stunden. Wie viel Zeit würden 7 Bagger benötigen?
Hierbei handelt es sich um einen antiproportionalen Dreisatz, denn je mehr Bagger eingesetzt werden, desto weniger Zeit wird insgesamt benötigt.
- 3 Bagger benötigen 21 Stunden
- Zeit, die ein Bagger benötigt: 21 h • 3 = 63 h
- Zeit, die 7 Bagger benötigen: 63 h : 7 = 9 h
Antwort: 7 Bagger benötigen 9 Stunden, um das Waldstück zu roden.
Dreisatzrechnung – FAQ
Was ist ein Dreisatz in der Mathematik?
Die Dreisatzrechnung ist ein bekanntes und oft eingesetztes Lösungsverfahren in der Mathematik. Mit ihm kannst du aus dem Verhältnis zweier bekannter Größen eine unbekannte Größe ausrechnen.
Beispiel: 3 Tafeln Schokolade kosten 5 Euro. Wie viel kosten 7 Tafeln Schokolade?
Mit Hilfe dieser kannst du 3 verschiedene Einheiten überschlagen und die 4. unbekannte ausrechnen. Er hilft die zudem in deinem Alltag. Durch seine Unterstützung ist es möglich Fragen wie z.B. “Reicht mein Geld für den Einkauf noch aus?” zu beantworten.
Wie wird der Dreisatz berechnet?
Der Dreisatz wird durch 3 einfache Schritte berechnet:
-
- Ausgangssituation angucken → Auf welche Zahl muss ich runden?
- Reduzierung auf eine Einheit
- Auf die gesuchte Zahl vervielfachen
Wie erkennt man einen umgekehrten Dreisatz?
Einen umgekehrten (=antiproportionalen) Dreisatz erkennt man daran, dass gilt: “Je mehr, desto weniger“. Das heißt, je mehr Wert X steigt, desto mehr sinkt Wert Y (und umgekehrt ebenso).
Ein Beispiel für einen umgekehrten Dreisatz ist die Anzahl ein Baggern, um ein Waldstück zu roden. Je mehr Bagger (= Wert X) im Einsatz sind, desto weniger Zeit (= Wert Y) benötigt die Rodung insgesamt.
Wie rechnet man einen antiproportionalen Dreisatz?
Bei einem antiproportionalen Dreisatz ist es wichtig, zu berücksichtigen, dass “Je mehr, desto weniger” gilt. Beide Seiten müssen also gegenteilig berechnet werden. Wird die eine Seite durch 3 dividiert, musst die andere Seite mit 3 multipliziert werden.

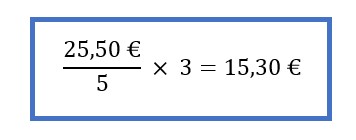



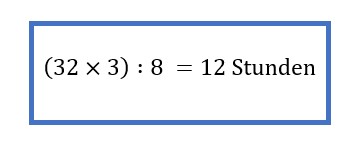
Sehr gut erklärt; war für mich eine schöne Auffrischung!
Mach ne Umschulung ins kaufmännische mit 46. Ihr glaubt ja nicht was man alles vergisst …
Danke ihr helft mir sehr weiter
Vielen Dank! Vertretungsstunde, kein Material zur Hand und nicht vom Fach. Half mir enorm!
Danke!Jetzt kann ich bei meinen Kindern wieder mitreden:)
Super verständlich erklärt. Vielen Dank für die Auffrischung aus der lang zurückliegenden Schulzeit;-D
War gut
Gut und ausführlich erklärt. Vor gefühlten 100 Jahren 😉 kannte man die Tabelle nicht, sondern verwendete gleich die Formel. Als NHL muß ich aber erst mal die Tabelle erklären.
Hat mir sehr geholfen.
war gut
Danke, es hat mir sehr geholfen.Jetzt kann ich mit meiner Enkelin wieder Schritt halten.
Danke das hat mir echt super geholfen!
Anschaulich und leicht verständlich.
War ganz gut erklärt,vielen Dank