5,00 von 5 Sterne
Loading...
Du bist dir unsicher, was genau ein Drachenviereck ist? Du möchtest wissen, wie man es berechnet? Dann bist du hier richtig!
Wir geben dir eine einfache Erklärung zum Drachenviereck, seinen Eigenschaften und Formeln und was der Unterschied zu anderen Vierecken ist.
Lass uns starten!
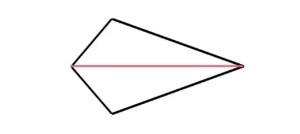
Ein Drachenviereck (Deltoid) ist eine besondere Art von Viereck. Du kennst sicher die Form dieses Vierecks von den Drachen, die wir im Herbst in den Himmel steigen lassen.
So sieht es aus:
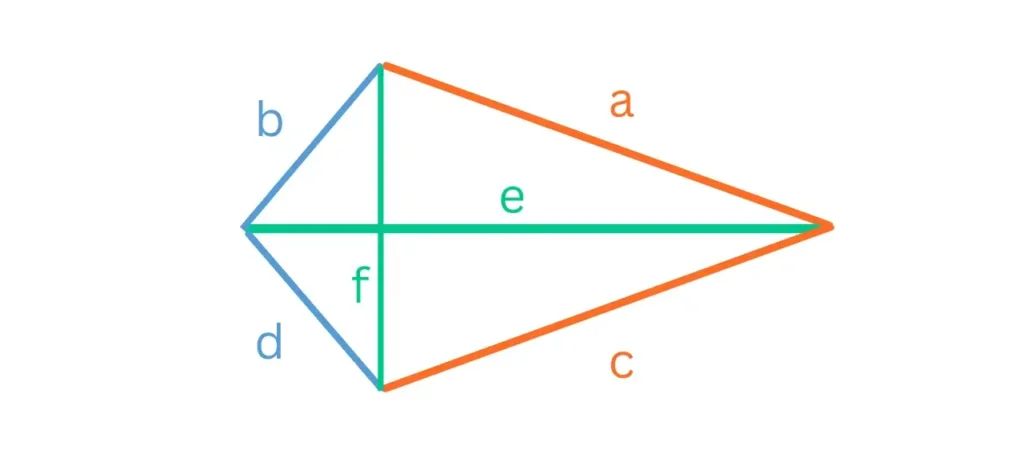
Drachenviereck Eigenschaften
Schauen wir uns nun die Eigenschaften des Drachenvierecks genauer an:
Seitenlängen
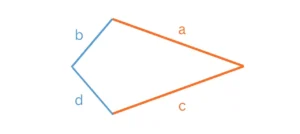
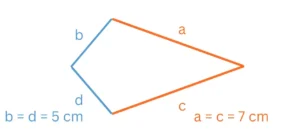
Wie bereits erwähnt, weist ein Drachenviereck zwei Seitenpaare auf, die jeweils gleich lang sind und sich gegenseitig berühren. In diesem Beispiel sind die Seiten a und d sowie die Seiten b und c gleich lang (a=c, b=d).
Winkel
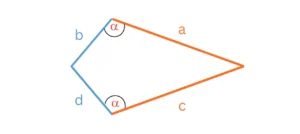
Das Drachenviereck besitzt zwei gleich große Winkel. Das sind die Winkel α, die jeweils zwischen der langen und der kurzen Seite liegen.
Diagonalen
Die Diagonalen verbinden jeweils einen Eckpunkt mit seinem gegenüberliegenden Eckpunkt.
Die Diagonalen besitzen folgende Eigenschaften:
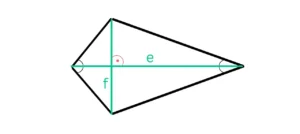
- Die Diagonalen e und f stehen senkrecht aufeinander und bilden einen rechten Winkel.
- Die lange Diagonale e halbiert die Winkel, die jeweils zwischen den beiden langen und den beiden kurzen Seiten liegen, und teilt auch die kurze Diagonale f genau in der Mitte.
- Die lange Diagonale e ist die Symmetrieachse des Drachenvierecks und teilt es in zwei gleich große, kongruente Dreiecke.
Achsensymmetrie
Jedes Drachenviereck ist achsensymmetrisch. Dabei ist immer die lange Diagonale die Symmetrieachse des Drachenvierecks und teilt es in zwei gleich große, kongruente Dreiecke.
Flächeninhalt Drachenviereck
Wie wir bereits gesehen haben, spielen die Diagonalen eine wichtige Rolle im Drachenviereck. Sie sind auch entscheidend, um den Flächeninhalt berechnen zu können.
Die allgemeine Formel für den Flächeninhalt A des Drachenvierecks lautet:
Nun musst du nur noch die Werte für die Diagonalen e und f einsetzen und kannst den Flächeninhalt ausrechnen.
Beispiel: Flächeninhalt Drachenviereck berechnen in 2 Schritten
Gegeben sei ein Drachenviereck ABCD mit den Diagonalen e = 6 cm und f = 4 cm. Wie groß ist der Flächeninhalt A des Drachenvierecks ABCD?
Schritt 1:
Zuerst brauchst du die allgemeine Formel für den Flächeninhalt A des Drachenvierecks. Die beste Methode ist es, diese auswendig zu lernen.
A = 1/2 • e • f
Schritt 2:
Setze die Werte der Diagonalen e= 6 cm und f= 4 cm in die Formel ein und rechne das Ergebnis aus.
A = 1/2 • 6 cm • 4 cm = 12 cm²
Der Flächeninhalt des Drachenvierecks ABCD beträgt 12 cm².
Umfang Drachenviereck
Die Formel zur Berechnung des Umfangs U eines Drachenvierecks addiert die Längen aller vier Seiten:
Da wir bereits wissen, dass die Seiten a und c sowie b und d gleich lang sind, können wir die Formel auch so schreiben:
Beispiel: Umfang Drachenviereck berechnen in 2 Schritten
Gegeben sei das folgende Drachenviereck ABCD:
Berechne den Umfang U des Drachenvierecks.
Schritt 1:
Zunächst brauchst du die allgemeine Formel für den Umfang U eines Drachenvierecks. Auch diese solltest du am besten auswendig lernen.
U = 2a + 2b
Schritt 2:
Setze die gegebenen Werte a und b in diese Formel ein:
U = 2 • 7 cm + 2 • 5 cm = 14 cm + 10 cm = 24 cm
Der Umfang U dieses Drachenvierecks beträgt 24 cm.
Inkreis des Drachenvierecks
Der Inkreis einer geometrischen Figur berührt jede Seite der Figur genau einmal.
Auch das Drachenviereck besitzt einen solchen Inkreis. Der Mittelpunkt des Kreises ist der Schnittpunkt der Winkelhalbierenden (nicht Diagonalen!). Die Winkelhalbierenden sind alle Geraden, die die vier Winkel des Drachens halbieren.
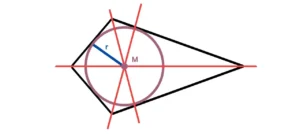
Den Radius vom Inkreis berechnest du mit folgender Formel:
In unserem Beispiel setzt du nun A = 20 cm² und U = 16 cm ein:
r = (2 • 20 cm²) /16 cm = 2,5 cm
Der Inkreis-Radius des Drachenvierecks beträgt 2,5 cm.
Einordnung als Viereck
Ein Drachenviereck ist eine besondere Form des allgemeinen Vierecks mit zwei gleich langen Seiten und einer Diagonalen als Symmetrieachse.
Wenn ein Drachenviereck vier gleich lange Seiten hat, ist es eine Raute. Da alle Seiten genau gleich lang sind, sind bei einer Raute beide Diagonalen Symmetrieachsen.
Wenn ein Drachenviereck vier gleich lange Seiten und vier rechte Winkel hat, ist es ein Quadrat. Bei einem Quadrat sind wie bei einer Raute beide Diagonalen Symmetrieachsen.
Übungsaufgaben
Lösung
U = 2a + 2b
U = 2 • 4 cm + 2 • 2 cm = 8 cm + 4 cm = 12 cm
Lösung
A = 1/2 • e • f
A = 1/2 • 5 cm • 2 cm = 5 cm²
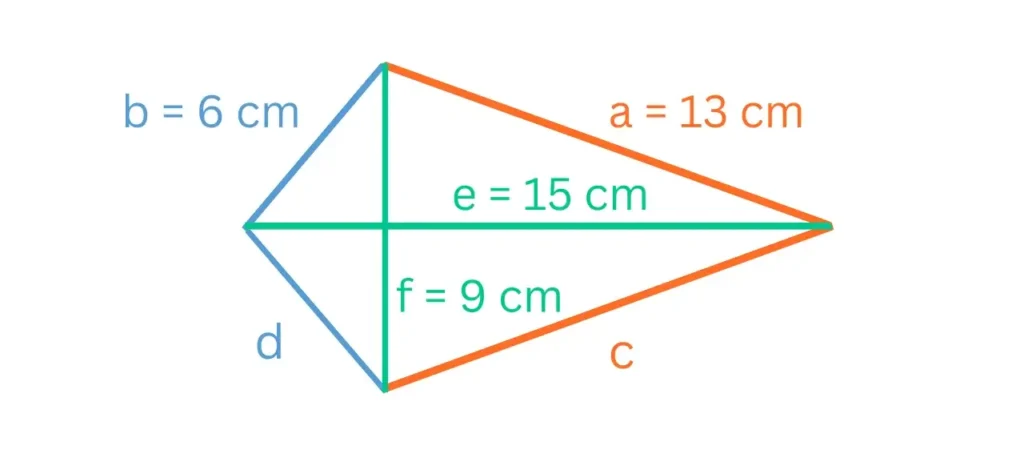
Lösung
U = 2a + 2b = 2 • 13 cm + 2 • 6 cm = 38 cm
A = 1/2 • e • f = 1/2 • 15 cm • 9 cm = 67,5 cm²
FAQ
Was ist ein Drachenviereck einfach erklärt?
Ein Drachenviereck ist ein spezielles Viereck, bei dem jeweils zwei anliegende Seiten gleich lang sind und eine Diagonale Symmetrieachse ist.
Was ist das Besondere an einem Drachenviereck?
Ein Drachenviereck besitzt folgende Eigenschaften: je zwei benachbarte Seiten sind gleich lang, die Diagonalen e und f stehen senkrecht aufeinander, die Winkel zwischen kurzer und langer Seite sind jeweils gleich groß, es ist achsensymmetrisch zur längeren Diagonalen.
Ist ein Drachenviereck auch eine Raute?
Nicht jedes Drachenviereck ist auch eine Raute. Die Raute ist eine besondere Form des Drachenvierecks, bei der nicht nur jeweils zwei anliegende Seiten, sondern alle vier Seiten gleich lang sind.
Ist eine Raute ein Drachenviereck?
Jede Raute ist auch ein Drachenviereck, da eine Raute alle Eigenschaften eines Drachenvierecks erfüllt.
Welche Winkel sind bei einem Drachenviereck gleich groß?
Bei einem Drachenviereck sind die beiden Winkel jeweils zwischen der längeren und der kürzeren Seite gleich groß. Diese Winkel sind gegenüberliegend.
Hast du noch weitere Fragen oder Tipps zur Berechnung des Drachenvierecks? Lass es uns in den Kommentaren wissen!
Wir haben diesen Artikel mit viel Mühe und Sorgfalt für dich erstellt. Wenn du ihn hilfreich fandest, würden wir uns sehr über eine Sternebewertung freuen. Vielen Dank!
5,00 von 5 SterneLoading...
