Distributivgesetz – simple Erklärung und Beispiele

Klammern setzen, Klammern auflösen? Diese Sachen bereiten dir Kopfschmerzen?

Keine Sorge, in diesem Artikel erklären wir dir das Distributivgesetz sehr einfach mit Hilfe von verständlichen Beispielen und Übungen.

Legen wir direkt los!

Distributivgesetz in Mathe – einfach erklärt

Als Distributivgesetz versteht man in der Mathematik die Rechenregeln, die du brauchst, um Klammern zu setzen und aufzulösen.

Es wird auch Verteilungsgesetz genannt.

Was ist das Distributivgesetz?

Stell dir mal vor, du musst folgende Aufgabe lösen:

4×(3+5)=?

Normalerweise berechnest du jetzt zuerst die Klammer (3+5)=8. Daraufhin multiplizierst du 4×8=32.

Mithilfe des Distributivgesetzes kannst du das aber auch anders lösen. Hierfür multiplizierst du die 4 mit den jeweiligen Werten in der Klammer. Du rechnest also 4×3 und 4×5 und addierst anschließend.

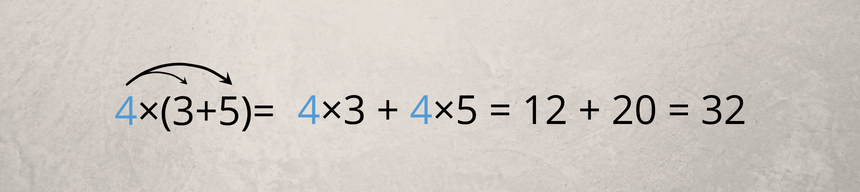
Du kannst also sehen, dass du mit beiden Rechenwegen auf das gleiche Ergebnis kommst, also 32.

Das Verteilungsgesetz besagt also, dass du eine Zahl anstatt mit einer Summe auch mit den einzelnen Summanden (die Zahlen in der Klammer) multiplizieren kannst.

Das funktioniert übrigens genauso, wenn du ein Minus in der Klammer stehen hast.

Division einfach gemacht mit dem Distributivgesetz

Bei der Division funktioniert das Ganze genau so wie bei der Multiplikation.

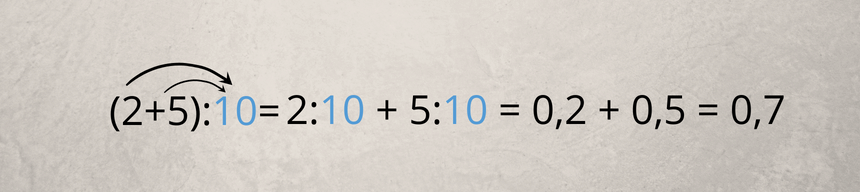
Ausklammern leicht gemacht mittels Distributivgesetz

Es gibt 2 weitere Begriffe, die im Zusammenhang mit dem Distributivgesetz vorkommen: Ausmultiplizieren und Ausklammern.

Das Ausmultiplizieren ist nichts anderes, als Klammern aufzulösen. Also das, was wir oben bereits dargestellt haben.

Beim Ausklammern musst du das Verteilungsgesetz “rückwärts” anwenden. Wenn die Glieder einer Summe bzw. Differenz gleiche Faktoren enthalten, kannst du diese Summe bzw. Differenz in ein Produkt umwandeln.

Du dividierst die einzelnen Glieder durch den gemeinsamen Faktor, klammerst die Summe bzw. Differenz der Ergebnisse ein und schreibst den gemeinsamen Faktor vor die Klammer.

An einem Beispiel würde das so aussehen:

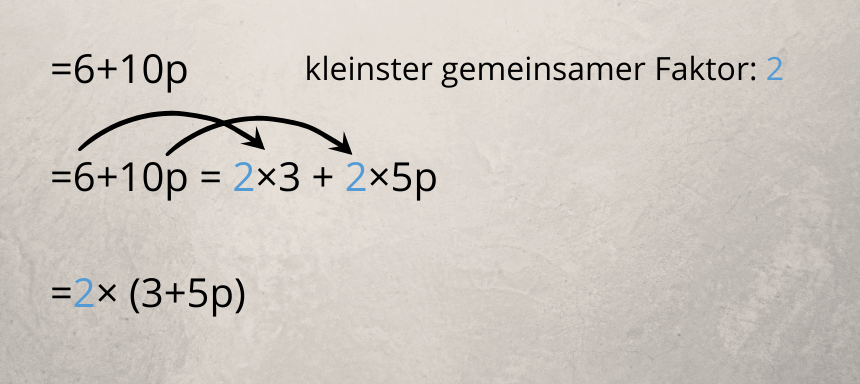
Der simple Merksatz für das Distributivgesetz

Diese Formeln kannst du immer benutzen, wenn du das Distributivgesetz benutzen willst.

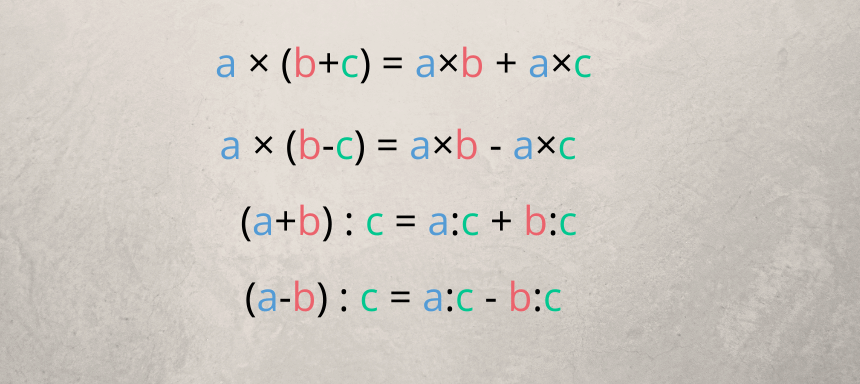
Wo gilt das Distributivgesetz nicht?

Wie wir oben bereits festgestellt haben, gilt es nicht bei Divisionen, bei denen die Klammer hinter dem Rechenzeichen “:” steht.

Außerdem gilt es nicht, wenn sich in den Klammern eine Multiplikation oder Division befindet. Hier kannst du zwar die Klammern trotzdem auflösen, allerdings nicht mit dem Distributivgesetz.

Fazit

Wie du also sehen kannst, ist es ganz einfach, das Distributivgesetz zu verstehen und anzuwenden. Mit ein wenig Übung wirst du in Zukunft sicherlich keine Probleme mehr damit haben.

Falls du dein Wissen zu den anderen Rechenregeln etwas auffrischen willst, kannst du das in diesen Beiträgen zu dem Assoziativgesetz und dem Kommutativgesetz tun.

Im Folgenden haben wir dir noch ein paar Übungen mit Lösungen zusammengestellt, um deine neu gewonnen Erkenntnisse zu vertiefen.

Viel Erfolg! 🙂

Distributivgesetz Aufgaben – verständlich dargestellt

Hinweis: Durch Klicken auf das + Symbol wird dir die Lösung angezeigt.