Brüche subtrahieren – Einfache Anleitung, Beispiele und Übungen

Du siehst Brüche und denkst dir: „Hilfe!“? Du weißt nicht, wie und wo du anfangen sollst? Insbesondere, wenn du Brüche subtrahieren musst?

Dann bist du hier richtig. Hier zeige ich dir, wie du mit Brüchen umgehst. Dabei schauen wir uns speziell die Subtraktion von Brüchen an.

Na, bereit Brüche zu subtrahieren? Dann los!

Büche subtrahieren – Was ist ein Bruch?

Ein Bruch beschreibt immer einen Teil von einem Ganzen, das heißt man spricht bei einem Bruch von einer Division. Der Bruch besteht immer aus drei Komponenten: Nenner, Zähler und dem Bruchstrich.

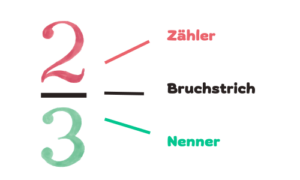
Dabei gibt der Nenner an, in wie viele gleich große Teile das Ganze geteilt wird. Der Zähler hingegen zeigt nur die Teile an, die gewählt wurden. Der Bruchstrich trennt die zwei Komponenten voneinander und symbolisiert die Division.

Das heißt man kann Brüche ausrechen.

\frac{1}{2} = 1 : 2 = 0,5

\frac{1}{2} = 1 : 4 = 0,25

\frac{1}{4} = 1 : 5 = 1,25

Brüche subtrahieren – So funktioniert’s!

Sowohl beim Addieren als auch beim Subtrahieren von Brüchen gibt es eine Besonderheit.

Gleichnamige Brüche

Bei gleichnamigen Brüchen müssen die Nenner gleich sein. Wenn die Nenner beider Brüche gleich sind, werden die Zähler subtrahiert und der Nenner der Brüche wird beibehalten.

Zum Beispiel:

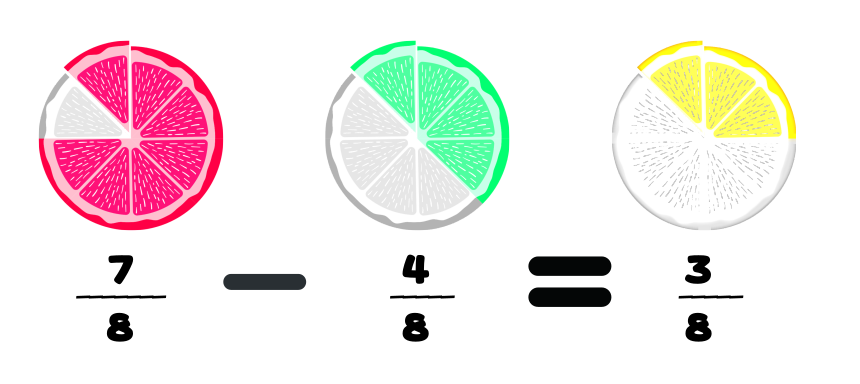
Ungleichnamige Brüche

Wenn die Brüche ungleichnamig sind, müssen diese erst gleichnamig gemacht werden. Das heißt sie auf einen gemeinsamen Nenner zu bringen, den sogenannten Hauptnenner.

Ganz wichtig: Ungleichnamige Brüche dürfen nicht sofort subtrahiert werden.

Um zu Subtrahieren, müssen die Brüche auf einen gemeinsamen Nenner erweitert werden. Der Zähler wird subtrahiert und der gleichnamige Nenner wird erhalten.

Zu jeder Möglichkeit habe ich hier ein Beispiel für dich:

Ein Nenner ist ein Vielfaches des anderen Nenners. Das heißt, dass der größere Nenner schon der gemeinsame Nenner der beiden Brüche ist.

Bei der zweiten Möglichkeit ist der größere Nenner kein Vielfaches des kleineren Nenners. Das heißt, dass die Nenner mit dem jeweiligen anderen Nenner erweitern werden müssen. Das sieht in der Praxis folgendermaßen aus:

Es wird auch vorkommen, dass beide Nenner groß sind. Dann ist es lohnend, nach einem gemeinsamen Vielfachen der beiden Nenner zu suchen.
Zum Beispiel:

Was wir gelernt haben ist, dass es bei der Subtraktion genau wie bei der Addition wichtig, dass die Nenner gleichnamig sind. Wenn diese es nicht sind, müssen sie gleichnamig gemacht werden.

Halten wir die wichtigsten Punkte zusammen fest:

Gleichnamige Brüche

• der Nenner wird beibehalten
• die Zähler werden subtrahiert

Ungleichnamige Brüche

• die Nenner müssen erweitert werden, d.h.  gleichnamig gemacht
• beim Erweitern werden auch die Zähler erweitert
• der gemeinsame Nenner wird beibehalten
• die Zähler werden voneinander subtrahiert

Hier findest du Aufgaben, die dir beim Üben helfen werden.
Klicke einfach auf die Links und schon öffnen sich PDFs mit Übungsaufgaben:
Brüche subtrahieren – Aufgaben.

Versuche zuerst selbst, die Aufgaben zu lösen.

Danach findest du hier die Lösungen:
Brüche subtrahieren – Lösungen. 

Viel Erfolg!

Brüche subtrahieren – FAQ

Hier findest du die weiteren Grundrechenarten mit Brüchen: