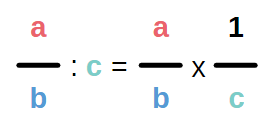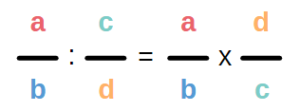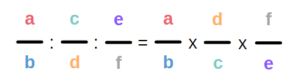Brüche dividieren – das Thema begleitet uns das ganze Leben und taucht immer wieder irgendwo auf. Daher ist es wichtig, dieses Thema problemlos zu beherrschen und sich einzuprägen. Wie Du Brüche dividieren und es nie mehr vergessen kannst, erfährst Du hier im folgenden Artikel.
Im Folgenden zeigen wir Dir,…
– … wie man Brüche allgemein teilt,
– … wie die Division von Brüchen mit ganzen Zahlen abläuft,
– … wie Brüche durch Brüche dividiert werden,
– … wie die Teilung von drei Brüchen funktioniert
– … und schließlich Aufgaben fürs eigene Training.
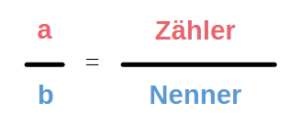
Brüche teilen – was bedeutet das überhaupt?
Bevor man damit beginnt, Brüche zu dividieren, sollte man zuerst im Kopf haben, wie ein Bruch überhaupt aussieht. Ein Bruch besteht aus einem Zähler (obere Zahl über dem Bruchstrich) und einem Nenner (untere Zahl unter dem Bruchstrich). Wie man mit einem Bruch teilt, erfährst Du nun im nächsten Kapitel.
Wie dividiert man einen Bruch?
Das Ergebnis eines Bruches erhält man, indem man die Zahl, die im Zähler steht, mit der Zahl, die im Nenner steht, teilt. Der Bruchstrich stellt nichts anderes als eine Division dar.
Beispiel:
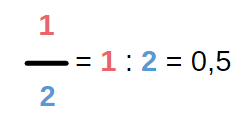
Negative Brüche dividieren
Wenn zwei Brüche, die dividiert werden, dasselbe Vorzeichen besitzen (beide positiv oder negativ), so ist das Ergebnis positiv. Wenn aber die zwei Brüche nicht dasselbe Vorzeichen haben (einer positiv und einer negativ), ist das Ergebnis negativ.
Brüche dividieren mit ganzen Zahlen – wie funktioniert das genau?
Jetzt kannst Du schon einmal Brüche dividieren, allerdings nur durch sich selbst. Doch was ist, wenn man einen Bruch durch eine ganze Zahl teilen möchte? Wie das klappt, erfährst Du im nächsten Kapitel.
Wie teile ich einen Bruch durch eine ganze Zahl?
Um einen Bruch durch eine ganze Zahl zu teilen, musst Du drei Schritte ausführen:
1. Die gegebene ganze Zahl in einen Bruch umwandeln.
2. Den Kehrwert davon bilden, also den Zähler und den Nenner tauschen.
3. Die beiden Brüche miteinander multiplizieren.
Beispiel:
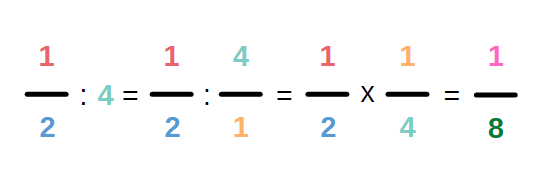

Brüche durch Brüche teilen – simpel und übersichtlich erklärt
Nachdem Du nun weißt, wie man einen Bruch durch eine ganze Zahl teilt, geht es jetzt darum, wie man einen Bruch durch einen anderen Bruch bzw. durch zwei andere Brüche dividieren kann. Wie das funktioniert, siehst Du in den nächsten Kapiteln.
Wie teilt man einen Bruch durch einen Bruch?
Um einen Bruch durch einen anderen Bruch zu dividieren, musst Du nur zwei Schritte durchführen:
1. Den Kehrwert des zweiten Bruches bilden, also den Zähler und den Nenner tauschen.
2. Die beiden Brüche miteinander multiplizieren.
Beispiel:
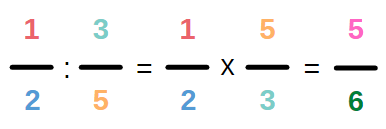

Wie dividiert man drei Brüche?
Darüber hinaus kann man auch mehrere Brüche dividieren. Um bspw. einen Bruch durch zwei andere Brüche zu teilen, musst Du auch nur zwei Schritte durchführen:
1. Den Kehrwert des zweiten und dritten Bruches bilden, also den Zähler und den Nenner tauschen.
2. Die drei Brüche miteinander multiplizieren.
Beispiel:
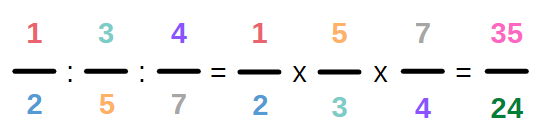
Auch wenn immer mehr Brüche dazukommen, die miteinander dividiert werden sollen, ändert sich das Vorgehen nicht. Um mehrere Brüche zu dividieren, werden immer die Kehrwerte aller Brüche außer der Kehrwert des ersten Bruches gebildet und schließlich alle vorhandenen Brüche miteinander multipliziert.

Brüche dividieren Aufgaben zur schnellen Selbstkontrolle
Falls Du Deine erlernten Kenntnisse zum Thema “Brüche dividieren” vertiefen möchtest, kannst Du hier mit dieser Übung Dein erlerntes Wissen mithilfe eines Klicks auf das jeweilige Plus anwenden. Mit den Lösungen kannst Du Deine Ergebnisse durch einen Klick auf das jeweilige Plus überprüfen. Weitere Aufgaben zum Brüche dividieren findest Du im Link.
3
— : 7 = ?
2
4 1
— : — = ?
9 6
2 8 10
— : — : — = ?
5 11 13
1
— : 9 = ?
4
2 8 5
— : — : — = ?
7 3 4
17 15 13 11
— : — : — : — = ?
16 14 12 10
3 3 7 3 1 3
— : 7 = — : — = — x — = —
2 2 1 2 7 14
4 1 4 6 24
— : — = — x — = —
9 6 9 1 9
2 8 10 2 11 13 286 143
— : — : — = — x — x — = —— = —
5 11 13 5 8 10 400 200
1 1 9 1 1 1
— : 9 = — : — = — x — = —
4 4 1 4 9 36
2 8 5 2 3 4 24 3
— : — : — = — x — x — = — = —
7 3 4 7 8 5 280 35
17 15 13 11 17 14 12 10 28560 119
— : — : — : — = — x — x — x — = ——— = —
16 14 12 10 16 15 13 11 34320 143
Brüche dividieren – Häufig gestellte Fragen / FAQ
Man dividiert zwei Brüche, indem man zuerst den Kehrwert des zweiten Bruches bildet, also den Zähler und den Nenner dieses Bruches tauscht, und dann beide Brüche miteinander multipliziert.
Man dividiert einen Bruch durch eine ganze Zahl, indem man zuerst aus der ganzen Zahl einen Bruch bildet. Wenn das geschehen ist, wird aus dem gerade entstandenen Bruch der Kehrwert genommen, also Zähler und Nenner wechseln ihre Plätze. Zum Schluss multipliziert man diesen Kehrwert mit dem anderen gegebenen Bruch.
Man dividiert drei Brüche, indem man zuerst den Kehrwert des zweiten und des dritten Bruches bildet, also den Zähler und den Nenner dieser Brüche tauscht, und dann alle drei Brüche miteinander multipliziert.
Falls zwei Brüche, die durcheinander geteilt werden, dasselbe Vorzeichen haben, so ist das Ergebnis positiv. Falls aber die zwei Brüche nicht dasselbe Vorzeichen besitzen, so ist das Ergebnis negativ.
Hat Dir der Inhalt geholfen? Lass uns gerne einen kurzen Kommentar da, wir würden uns sehr freuen! Ansonsten findest Du weitere hilfreiche Erklärungen zu verschiedenen Themengebieten auf der Homepage des Nachhilfe-Teams.