4,50 von 5 Sterne
Loading...
Der Binomialkoeffizient ist ein zentrales Konzept der Kombinatorik. In der Schule kommen wir deswegen nicht drum herum uns das ganze mal genauer anzugucken. Doch auch im Alltag spielt der Binomialkoeffizient oft eine Rolle, auch wenn man das vielleicht erstmal nicht auf dem Schirm hat. Wir verbinden beides und schauen uns an:
- wie der Binomialkoeffizient funktioniert und was er überhaupt ist
- Berechnung mit und ohne Taschenrechner
- praktische Beispiele zum optimalen Verständnis
- die wichtigsten Rechenregeln
- Aufgaben für die perfekte Prüfungsvorbereitung
Los geht’s!
Bei dir läuft’s! Du hast sowohl Kekse als auch deine Freunde am Start. Jetzt ist aber das Blöde, dass die Anzahl der Freunde und die Anzahl von Keksen nicht gleich sind.
Du würdest die Kekse gerne verteilen und gehst die einzelnen Möglichkeiten dafür durch und dir kommt folgende Frage in den Kopf: Wie viele Möglichkeiten gibt es eigentlich, die Kekse zu verteilen?
Genau hier kommt der Binomialkoeffizient ins Spiel. Mit diesem können wir die Frage ganz einfach beantworten:
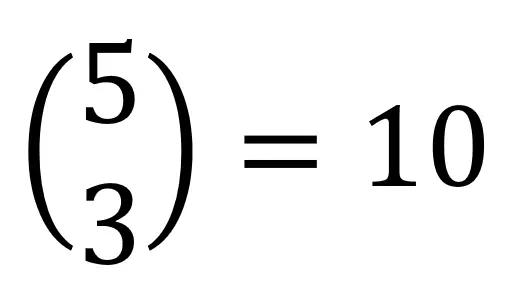
Es gibt also genau 10 Möglichkeiten, die 5 Kekse unter deinen 3 Freunden aufzuteilen. Jetzt haben wir bis zum Ergebnis aber ein paar Schritte übersprungen, schauen wir uns das nochmal in Ruhe an.
Binomialkoeffizient Definition
Fangen wir mal ganz vorne an. Das sieht sehr mathematisch aus, aber da müssen wir jetzt einmal zusammen durch, um alles gut verstehen zu können. Aber keine Sorge, das ist viel einfacher als man denkt!
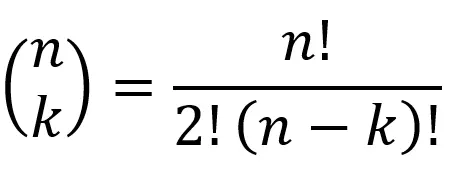
Der Binomialkoeffizient ist eine mathematische Funktion. Hinter den zwei Buchstaben in der Klammer versteckt sich also eine ganze Formel.
n und k stehen dabei jeweils für die Anzahl von Objekten, die man betrachtet.
Binomialkoeffizient berechnen – so einfach geht’s
Jetzt wissen wir schon mal, worum es eigentlich geht. Schauen wir uns nun mal an, wie wir den Binomialkoeffizienten am einfachsten berechnen:
Binomialkoeffizient ohne Taschenrechner berechnen
Um den Binomialkoeffizienten ohne Taschenrechner zu berechnen, braucht es gar nicht viel.
Beispiel: Wir wollen den Binomialkoeffizienten 
berechnen
Wir notieren uns schon mal: n = 4 und k = 2. Die Werte müssen wir dann nur noch in unsere Formel einsetzen:
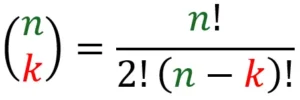
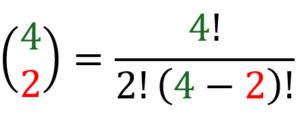
Ist das geschafft, lösen wir als nächstes die Klammer auf und kümmern uns um die Fakultäten.
Das sieht doch schon mal besser aus! Wir rechnen nun als nächstes einfach alles unter und über dem Bruchstrich zusammen.
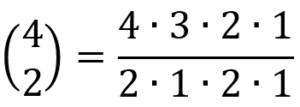
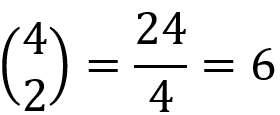
Den Bruch können wir noch in eine ganze Zahl umwandeln und dann sind wir in 3 Schritten auch schon fertig mit unserer Rechnung.
Binomialkoeffizient mit Taschenrechner berechnen
Wer es eilig und einen Taschenrechner hat, kann diesen selbstverständlich auch nutzen, um den Binomialkoeffizienten auszurechnen.
Bleiben wir dafür mal bei unserem Beispiel und nehmen uns den Binomialkoeffizienten
Beim Taschenrechner brauchen wir nun die “nCr”-Taste. Ist die gefunden, kann es auch schon losgehen!
Binomialkoeffizient Rechner – schnell zur Lösung
Wenn dir das selbst ausrechnen zu lange dauert, gibt es hier einen ganz einfachen Rechner für dich. Einfach n und k eingeben und der Binomialkoeffizient wird für dich ausgerechnet. Aber pass auf, in der Prüfung kannst du den leider nicht benutzen.
Binomialkoeffizient Aufgaben – Wissen testen und vertiefen
Aufgabe 1: Bei euch auf der Schule findet ein Fußballturnier statt. Bei dir in der Klasse sind tatsächlich 22 Fußballbegeisterte am Start, sodass euer Sportlehrer sich entschließt, 2 Teams teilnehmen zu lassen. Für das erste Team muss er nun 11 Spieler auswählen.
Berechne die Anzahl an Möglichkeiten mit Hilfe des Binomialkoeffizienten.
Lösung
Wir suchen 11 Spieler aus einer Gruppe von 22 Spielern. Wir schreiben den Binomialkoeffizienten 
Dies können wir dann mit Hilfe unserer Formel ausrechnen: 
Lösung: Der Sportlehrer hat 705.432 Möglichkeiten, das erste Team aus der Klasse von 22 auszuwählen. An Auswahl fehlt es dem Lehrer also nicht!
Aufgabe 2: Du kommst frisch aus dem Urlaub und möchtest ein paar Erinnerungen auf Instagram posten. Du hast 40 gute Freunde, von denen immer ungefähr die Hälfte einen Like gibt.
Wie viele Möglichkeiten gibt es, dass auch dein nächstes Foto 20 Likes von deinen Freunden sammelt?
Lösung
Wir brauchen 20 Likes von 40 möglichen, netten Freunden. Wir schreiben den Binomialkoeffizienten 
Dies können wir dann mit Hilfe unserer Formel ausrechnen: 
Lösung: Es gibt 137.846.528.820 Möglichkeiten, wie man mit dieser Anzahl an Freunden 20 Likes bekommt. Das sollte doch eigentlich machbar sein!
Binomialkoeffizient Rechenregeln
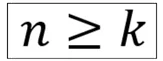
Diese Regel besagt, dass der Binomialkoeffizient nur definiert ist, wenn n größer oder gleich k ist. Das liegt daran, dass wir mit Binomialkoeffizienten k Objekte aus unseren n Objekten auswählen wollen. Da wir nicht mehr Objekte auswählen können, als es überhaupt gibt, ist der Bereich außerhalb nicht definiert.
Beispiel: Wenn du eine Packung mit nur 10 Keksen hast, kannst du nicht 12 herausnehmen.
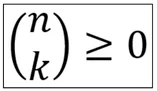
Da der Binomialkoeffizient immer die Anzahl an Möglichkeiten gibt, k Objekte aus einer Gruppe von n Objekten auszuwählen, kann dieser nicht negativ sein. Der Binomialkoeffizient ist somit immer positiv oder Null.
Beispiel: Egal ob wir 1,2,3 usw. Kekse aus unserer Packung nehmen wollen, die Anzahl an Möglichkeiten ist immer positiv.
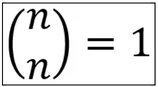
Hier gehen wir davon aus, dass n und k die gleiche Zahl sind. Ist dies der Fall, ist der Binomialkoeffizient immer 1.
Beispiel: Du möchtest alle Kekse aus der Packung mit 10 Keksen nehmen. Die einzige Möglichkeit, um dies zu tun ist, alle Kekse herauszunehmen.
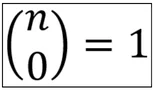
In dieser Regel ist k gleich 0. Wir suchen also die Anzahl an Möglichkeiten keine Objekte aus den anderen Objekten zu nehmen. Die einzig mögliche Antwort ist hier ebenfalls 1.
Beispiel: Du bist gar nicht hungrig und möchtest keinen Keks aus der Packung nehmen. Dabei hast du nur eine Möglichkeit dies zu tun: Die Packung stehen lassen und keinen Keks nehmen.
FAQ – wir klären die letzten Fragen
Was sagt der Binomialkoeffizient aus?
Der Binomialkoeffizient ist ein wichtiges Konzept der Kombinatorik und gibt an, wie viele Möglichkeiten es gibt k Objekte aus einer Menge von n Objekten auszuwählen. Die Auswahl erfolgt dabei ohne Zurücklegen und Beachtung der Reihenfolge.
Was ist n und k?
n steht für die Anzahl aller betrachteten Objekte und bildet somit die Grundgesamtheit. k gibt dann an, wie viele Objekte aus der Grundgesamtheit ausgewählt werden.
Wann wende ich den Binomialkoeffizient an?
Man wendet den Binomialkoeffizienten an, wenn man herausfinden will, wie viele Möglichkeiten es gibt k Objekte aus der Gesamtheit von n Objekten zu ziehen. Er ist dabei ein wichtiges Konzept der Kombinatorik und Wahrscheinlichkeitsrechnung.
Wir haben viel Mühe in diesen Artikel gesteckt und freuen uns riesig, wenn du uns eine Sternebewertung hinterlässt. Vielen Dank!
4,50 von 5 SterneLoading...
