Was war denn noch mal die bedingte Wahrscheinlichkeit, fragst du dich?
Die bedingte Wahrscheinlichkeit ist die Wahrscheinlichkeit, die unter der Bedingung eines vorherigen Ergebnisses einhergeht.
Was genau das bedeutet, wie du sie berechnest und darstellen kannst, das zeigen wir dir jetzt!
Beispiele für die bedingte Wahrscheinlichkeit
Um dir genauer zu zeigen, was die bedingte Wahrscheinlichkeit ist, gehen wir von einem Beispiel aus.
Stell dir vor, du ziehst aus einer Urne, in der 3 rote Kugeln, 3 grüne und 2 gelbe Kugeln sind. Du ziehst 2 Mal.
Jetzt möchtest du die Wahrscheinlichkeit dafür berechnen, dass du beim 2. Zug eine gelbe Kugel ziehst. Und genau das ist die bedingte Wahrscheinlichkeit.
Die Wahrscheinlichkeit beim 2. Zug eine gelbe Kugel zu ziehen, ist nämlich davon abhängig, welche Kugel du beim ersten Zug gezogen hast.
Bedingte Wahrscheinlichkeit Formel
Es gibt 2 verschiedene Schreibweisen für die bedingte Wahrscheinlichkeit. Das sind die geläufigsten, wobei wir hier für alles Weitere nun die 2. verwenden.
Dabei sagen beide Schreibweisen die Wahrscheinlichkeit für A unter der Bedingung, dass B eingetroffen ist, aus.
Die Formel für die bedingte Wahrscheinlichkeit sieht wie folgt aus:
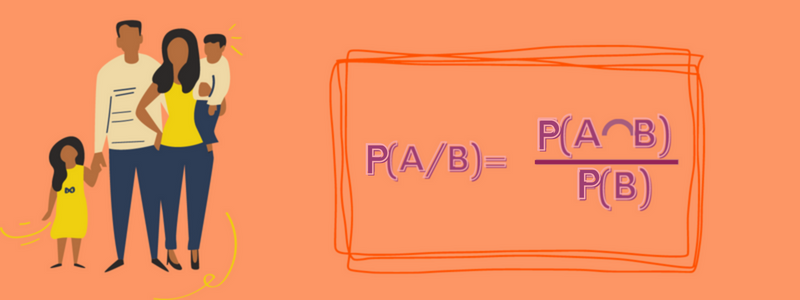
Sprich die Wahrscheinlichkeit der Schnittmenge von A und B geteilt durch die Wahrscheinlichkeit von B.
Bedingte Wahrscheinlichkeit Aufgaben
Bei der Bearbeitung von Aufgaben für die bedingte Wahrscheinlichkeit stößt man immer wieder auf Schwierigkeiten, vor allem beim Ablesen an der Vierfeldertafel oder dem Baumdiagramm.
Deshalb zeigen wir dir das jetzt anhand konkreter Beispiele!
Wie berechnet man die bedingte Wahrscheinlichkeit?
Gehen wir davon aus, dass du bei einem Gewinnspiel mitmachst. Hier ist deine Aufgabe, mit 2 Würfel Zügen eine Augenzahl von 8 zu würfeln.
Dein erster Wurf war eine 4. Du möchtest jetzt also die Wahrscheinlichkeit dafür berechnen, dass du eine Augenzahl von 8 würfelst, unter der Bedingung, dass dein erster Wurf eine 4 war.
Die einzige Option, jetzt also noch auf 8 zu kommen, wäre noch eine 4 zu würfeln.
Wir wissen außerdem, dass die Wahrscheinlichkeit eines Würfels für jede Zahl ⅙ ist.
Das bedeutet -> P(4)= ⅙
Daraus errechnen wir, dass P(4◠4)= P(4)*P(4)= 1/36
Und damit können wir nun P(4/4) berechnen. -> P(4/4)= ⅙
Wahrscheinlichkeit am Baumdiagramm darstellen
Am Baumdiagramm kannst du, wenn du es ganz ausgefüllt hast, die bedingte Wahrscheinlichkeit einfach ablesen oder damit einfach die bedingte Wahrscheinlichkeit darstellen.
Das ganze sieht wie folgt aus:
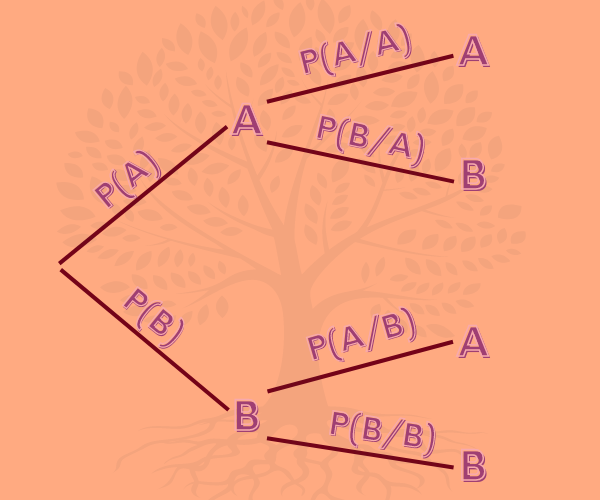
An der Vierfeldertafel
In der Vierfeldertafel kannst du zwar die bedingte Wahrscheinlichkeit nicht ablesen, hast aber direkt alle Angaben die du brauchst, um sie damit auszurechnen.
Die Vierfeldertafel sieht nämlich wie folgt aus:
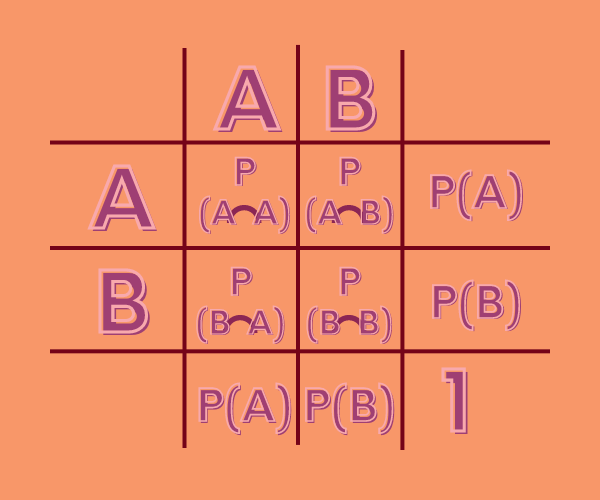
Daraus lässt sich dann mit der Formel die bedingte Wahrscheinlichkeit berechnen.
Das war die bedingte Wahrscheinlichkeit. Wenn du noch nicht genug hast, guck doch gerne bei unserem allgemeinen Artikel zur Wahrscheinlichkeit oder der Vierfeldertafel vorbei!
Überprüfe zum Schluss noch dein Wissen und bearbeite die Übungsaufgaben:
Du forscht an einem Medikament gegen Grippe und testest dieses an 800 Personen. Dabei haben nur 400 Personen das Medikament eingenommen. Nach einer gewissen Zeit guckst du dir jetzt an, wie viele erkrankt sind.
Von den 400 Leuten, die das Medikament genommen haben sind 60 Leute krank geworden. Von denen, die das Medikament nicht genommen haben sind 180 krank geworden.
Aufgabe:
Wie hoch ist die Wahrscheinlichkeit, dass man krank wird, unter der Bedingung das Medikament genommen zu haben und unter der Bedingung es nicht genommen zu haben?
15 % der Leute, die das Medikament genommen haben werden krank.
45% der Leute, die das Medikament nicht genommen haben werden krank.
Wir haben viel Mühe in diesen Artikel gesteckt und freuen uns riesig, wenn du uns eine Sternebewertung und einen Kommentar hinterlässt. Vielen Dank!
5,00 von 5 Sterne
Loading...
Loading...